
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Взаимодействия электронов с веществом.Прохождение электронов и позитронов через вещество отличается от прохождения тяжелых заряженных частиц. Главная причина - малая масса покоя электрона и позитрона. Это приводит к относительно большому изменению импульса при каждом столкновении, что вызывает заметное изменение направления движения электрона и как результат - электромагнитное радиационное излучение электронов. Второе отличие состоит в том, что движущиеся электроны тождественны атомным электронам, которым передается наибольшая часть энергии частиц, тормозящихся под действием кулоновских сил. При рассмотрении элементарного процесса взаимодействия двух электронов надо учитывать отклонение обеих частиц, а также квантово-механический эффект обмена, обусловленный их тождественностью. Упругое рассеяние электронов Дифференциальное микроскопическое поперечное сечение рассеяния электронов описывается выше приведенной формулой Резерфорда (3.81), которая в этом случае, принимая заряд электрона равный 1, обычно записывается в виде:
dσel(E/, μs)/d μs =πZа 2 e4/2E/2(1-μs)2 (3.88),
Для учета экранирования поля ядра атомными электронами используется параметр экранирования Мольера
а для учета рассеяния на атомных электронах используется замена Zа2 на Zа(Zа+1) в формуле (3.88). Квантовомеханическое рассмотрение рассеяния электронов с учетом волновых свойств, их спинов в приближении, что возмущение плоской волны рассеивающим атомом мало, позволило Мотту получить поправку R(E/, θs) к формуле Резерфорда: R(E/, θs)=1-β2(1-μs)/2+ 
В итоге можно записать модифицированную формулу Резерфорда для дифференциального микроскопического поперечного сечения рассеяния:
dσel(E/, μs)/d μs =Zа(Zа+1) R(E/, θs) e4/4E/2(1+2
Интегрирование по углу рассеяния дифференциального поперечного сечения позволяет получить формулу для полного микроскопического поперечного сечения упругого рассеяния электронов:
σel(E/ )= Zа(Zа+1) e4 [π/
Для расчета массовых потерь энергии при упругом рассеянии электрона можно воспользоваться формулой (3.82), заменив в ней параметры частицы на параметры электрона. |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 323. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
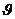 :
: (1,13 + 2*10-4
(1,13 + 2*10-4 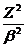 ) (3.89),
) (3.89), πβZa(1- μs)1/2[1-(1- μs)1/2/
πβZa(1- μs)1/2[1-(1- μs)1/2/  ] (3.90).
] (3.90).