
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Интегральная теорема ЛапласаСтр 1 из 2Следующая ⇒ Тема 7. Повторение испытаний (2 ч.) Формула Бернулли О. 1.Если проводится несколько испытаний, причем вероятность появления события Пусть проводится Условимся считать, что вероятность события Тогда вероятность ненаступления события Выше описанная совокупность условий называется схемой независимых испытаний Бернулли. Теорема 1. Если вероятность Пример 1. В результате обследования были выделены семьи, имеющие по четыре ребенка. Считая вероятность появления мальчика в семье равной 0.515, определить вероятность появления в ней двух мальчиков. Решение: Локальная теорема Муавра-Лапласа При больших Теорема 2. Если вероятность появления события
Для определения значений функции  Пример 2. Вероятность поражения мишени стрелком при одном выстреле равна Решение: Т. к. Тогда При этом вычисления по формуле Бернулли приводят к значению Формула Пуассона Если число испытаний Теорема 3. Если вероятность
Строго говоря, условие теоремы 2:
Пример 3. Завод отправил в торговую сеть 500 изделий. Вероятность повреждения изделия в пути равна 0.002. Найти вероятность того, что при транспортировке будет повреждено три изделия. Решение: В данном случае формула Бернулли не применима, т. к. придется возводить 0. 002 в 500-ю степень. Интегральная теорема Лапласа Пусть выполнены условия схемы независимых испытаний Бернулли, причем Теорема 4.Если вероятность появления события
Функцию Для определения значений функции Пример 4. Вероятность того, что деталь не пройдет проверку качества, равна Решение: Т. к. |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 244. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
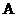 в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимымиотносительно события
в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимымиотносительно события 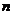 независимых испытаний, в каждом из которых возможно только два исхода: либо событие
независимых испытаний, в каждом из которых возможно только два исхода: либо событие 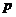 .
.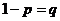 .
.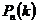 того, что в
того, что в 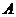 появится ровно
появится ровно 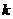 раз, вычисляется по формуле
раз, вычисляется по формуле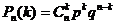 .
. .
.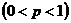 , то вероятность
, то вероятность 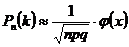 , где
, где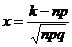 ,
, 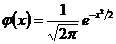 .
.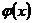 существуют специальные таблицы соответствующие положительным значениям аргумента
существуют специальные таблицы соответствующие положительным значениям аргумента 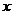 . При отрицательных значениях аргумента пользуются теми же таблицами, т. к.
. При отрицательных значениях аргумента пользуются теми же таблицами, т. к. 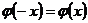 .
.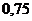 . Найти вероятность того, что при 100 выстрелах стрелок поразит мишень 80 раз.
. Найти вероятность того, что при 100 выстрелах стрелок поразит мишень 80 раз.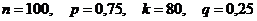 , то
, то  .
. .
.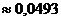 . Такие значительные расхождения связаны с недостаточно большим значением
. Такие значительные расхождения связаны с недостаточно большим значением 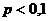 , то применение формулы Муавра-Лапласа становится невозможным.
, то применение формулы Муавра-Лапласа становится невозможным.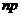 сохраняет постоянное значение, т. е.
сохраняет постоянное значение, т. е. 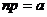 , то вероятность
, то вероятность 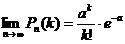 (2).
(2).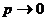 при
при 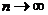 , нарушает исходные предпосылки в схеме независимых испытаний Бернулли, в которой
, нарушает исходные предпосылки в схеме независимых испытаний Бернулли, в которой 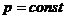 . Однако, если вероятность
. Однако, если вероятность 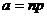 незначительно, то из предельного равенства (2) можно записать приближенную формулу Пуассона:
незначительно, то из предельного равенства (2) можно записать приближенную формулу Пуассона: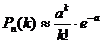 .
.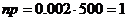 ;
; 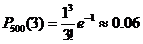 .
.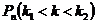 того, что в
того, что в 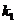 до
до 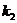 раз (не более
раз (не более 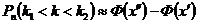 , где
, где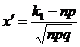 ,
, 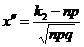 ,
, 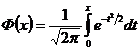 .
.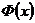 называют функцией Лапласа.
называют функцией Лапласа.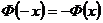 .
.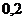 . Найти вероятность того, что из 400 проверенных деталей бракованными окажутся не более 70, но не менее 100 деталей.
. Найти вероятность того, что из 400 проверенных деталей бракованными окажутся не более 70, но не менее 100 деталей.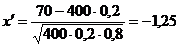 ,
, 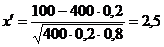 , то
, то 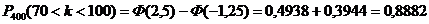 .
.