
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вычисление объема тел с помощью определенного интегралаСтр 1 из 2Следующая ⇒ Приложения определенного интеграла. Вычисление площадей плоских фигур 1.Если на отрезке [a, b] функция f(x) 2. Если на [a, b] функция f(x)
3. Если f(x) – конечное число раз меняет знак на [a, b], то интеграл есть алгебраическая сумма площадей, лежащих выше и ниже оси ОХ, то есть 4. Если нужно вычислить площадь области, ограниченной кривыми
По формуле (1) имеем:
Если плоская фигура ограничена линиями, заданными в параметрическом виде, то ее площадь находится с помощью замены переменной. Пусть кривая задана уравнениями y=f(t), x=φ(t). Отсюда dx=φ/(t)dt, Пример. Вычислить площадь фигуры, ограниченной эллипсом
Перепишем уравнение эллипса в параметрическом виде:
Тогда:
Площадь криволинейного сектора Пусть в полярной системе координат имеем кривую, заданную уравнением
1. Разобьем данную область на n частей радиус – векторами. 2. Обозначим через 3. Обозначим через 4. Вычислим площадь криволинейного сектора с радиусом
5. Составим сумму ступенчатого сектора: 
6. Перейдем к пределу при условии, что max
Длина дуги кривой Пусть дана кривая y=f(x). Найдем длину дуги кривой, заключенной между точками A и B. Для вычисления длины дуги разобьем ее на n частей точками A=М0,М1,М2,…, Мn=B.
Абсциссами данных точек будут a=x0, x1, x2,…,xn=b. Проведем хорды. Длины этих хорд обозначим через
Замечание 1. Так как подынтегральное выражение представляет собой:
есть дифференциал дуги АВ. Замечание 2. Если дуга АВ задана в параметрическом виде:
следовательно:
Замечание 3. Если дуга АВ задана в полярной системе координат, то используя связь между декартовой и полярной системами координат имеем:
Эти уравнения можно рассматривать, как параметрические, применив для них предыдущую формулу:
Пример. Вычислить длину дуги астроиды (это кривая, заданная уравнением Решение. В параметрическом виде уравнение имеет вид: L1=
= Следовательно:
Вычисление объема тел с помощью определенного интеграла Вообще объемы тел вычисляются с помощью кратных интегралов. С помощью определенного интеграла решается частная задача вычисления объема тела с известным поперечным сечением (в основном это объемы тел вращения). Пусть требуется вычислить объем тела, площадь поперечного сечения которого, известна. Пусть это тело заключено между параллельными плоскостями. Проведем ось, перпендикулярную этим плоскостям, и замерим расстояние вдоль оси между этими плоскостями. Пусть x=a и x=b отсюда r=[a; b]. Площадь поперечного сечения зависит от положения секущей плоскости, то есть зависит от х. Для вычисления объема тела сделаем следующее. 1. Проведем плоскости 2. Вычислим объем диска, заключенного между плоскостями 3. Если 4. Так как главная часть приращения функции есть дифференциал, то при 5. Вычислим интеграл от обеих частей этого равенства:
Этой формулой пользуются при вычислении объема тел вращения. Телом вращения называется тело, полученное при вращении криволинейной трапеции вокруг некоторой оси. Рассмотрим тело, полученное вращением вокруг оси ОХ криволинейной трапецией, ограниченной кривой y=f(x), осью ОХ и прямыми x=a и x=b. В этом случае проведенное сечение тела плоскостью, перпендикулярной к оси ОХ, есть круг, площадь которого равна:
Замечание. Если криволинейная трапеция вращается вокруг оси ОУ, то объем будет вычислен по формуле |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 506. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
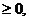 то площадь криволинейной трапеции будет равна
то площадь криволинейной трапеции будет равна  .
. , то
, то  .
.

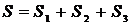 . Следовательно
. Следовательно  .
.
 ,
,  , причем
, причем  , и прямыми x=a и x=b, то имеем:
, и прямыми x=a и x=b, то имеем:
 .
.
 . (1)
. (1) Пример. Найти площадь области, ограниченной линиями
Пример. Найти площадь области, ограниченной линиями  .
. . Найдем пределы интегрирования:
. Найдем пределы интегрирования: ,
,  ,
, 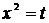 ,
,  ,
, ,
,  .
.

 (кв.ед).
(кв.ед). .
. и осью ОХ.
и осью ОХ.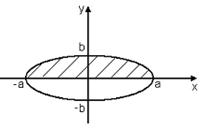


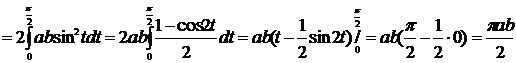 .
. где
где  - непрерывная функция,
- непрерывная функция,  . Определим площадь криволинейного сектора ОАВ, ограниченного кривой
. Определим площадь криволинейного сектора ОАВ, ограниченного кривой 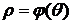 и радиус – векторами α и β.
и радиус – векторами α и β.
 углы между проведенными радиус – векторами.
углы между проведенными радиус – векторами. радиус – вектор, соответствующий углу
радиус – вектор, соответствующий углу 
 :
:
 .
. , получим:
, получим: .
.
 . Введем обозначения:
. Введем обозначения: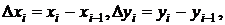
 Используя теорему Пифагора получим, что
Используя теорему Пифагора получим, что 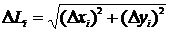 . Разделим обе части равенства на
. Разделим обе части равенства на  . Так как дуга гладкая, значит, в каждой ее точке существует производная, а следовательно к дроби
. Так как дуга гладкая, значит, в каждой ее точке существует производная, а следовательно к дроби  можно применить теорему Лагранжа
можно применить теорему Лагранжа  . Чтобы найти длину ломаной, стягивающей дугу AB нужно сложить все хорды, входящие в эту ломаную линию, то есть
. Чтобы найти длину ломаной, стягивающей дугу AB нужно сложить все хорды, входящие в эту ломаную линию, то есть  . Длиной дуги АВ называют тот предел, к которому стремится длина вписанной ломаной, когда длина ее наибольшего звена стремится к нулю. Для нахождения дуги АВ в последнем равенстве перейдем к пределу:
. Длиной дуги АВ называют тот предел, к которому стремится длина вписанной ломаной, когда длина ее наибольшего звена стремится к нулю. Для нахождения дуги АВ в последнем равенстве перейдем к пределу: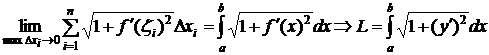
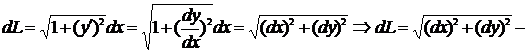



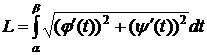 .
.

 ).
). а длина дуги астроиды равна L=4L1. Вычислим:
а длина дуги астроиды равна L=4L1. Вычислим:

 .
. .
.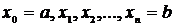 .
. ,
,  , то диск можно приблизительно считать цилиндрическим, тогда
, то диск можно приблизительно считать цилиндрическим, тогда 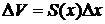 .
.
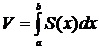 .
.

 где x=
где x=  ,
, 