
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Понятие о функциональной и корреляционной зависимости. Коэффициент корреляции, его оценка, метод расчета, значение, применение.Корреляция – понятие, которое также означает взаимосвязь между признаками. При корреляционных связях, характерных для медико-биологических явлений, значению одного признака соответствуют разные значения других признаков. Корреляционная связь необходима, например, при оценке взаимосвязей между стажем работы и уровнем заболеваемости работающих; между разными уровнями физических факторов окружающей среды и состоянием здоровья; между различными уровнями интенсивности нагрузки и частотой (уровнем) физиологических реакций организма; между сроками госпитализации и частотой осложнений. Статистика позволяет исследователю измерить связи, обосновать выводы и наглядно их иллюстрировать. Корреляционная связь бывает положительной - прямой (при увеличении одного признака увеличивается другой) и отрицательной - обратной (при увеличении одного показателя другой уменьшается). Коэффициент корреляции свидетельствует не только о направлении связи, но и об уровне этой связи. Сильная связь выражается коэффициентом от 0,7 до 0,99, средняя — от 0,3 до 0,69, слабая — до 0,29. При нулевом значении коэффициента связи отсутствуют. Известны два вида связи между явлениями (признаками): функциональная и корреляционная. Функциональная связь отражает строгую зависимость процессов или явлений и изменение какого-либо одного явления обязательно связано с изменением числовых значений другого явления на строго определенную величину. Функциональная связь, как правило, проявляется при физических и химических явлениях, где её можно представить в виде уравнения, формулы. Примеров функциональной связи может являться увеличение объема шара в строгой зависимости от увеличения его радиуса, расширение тела по мере увеличения температуры нагревания.  Наиболее часто применяемым методом получения поэф корел. Явл-ся способ квадратов (Пирсона) r= По методу Пирсона ошибка коэффициента корреляции вычисляется по формуле: mr = Второй метод получения коэф корел – метод рангов (Спирмена) Pxy=1- По методу Спирмена ошибка вычисляется по формуле: mp = Достоверность метод рангов t= |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 368. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
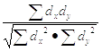 , x и y – признаки мезду кот опр-ся связь; dx и dy – отклонение каждой варианты от средней величины, вычисленной в ряду признака Х и y
, x и y – признаки мезду кот опр-ся связь; dx и dy – отклонение каждой варианты от средней величины, вычисленной в ряду признака Х и y
 ,где ху – признаки ,между кот опр-ся связь; 6- коэффициент; d –разность рангов; n- число наблюдений.
,где ху – признаки ,между кот опр-ся связь; 6- коэффициент; d –разность рангов; n- число наблюдений.
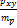 Метод квадратов t=
Метод квадратов t= 