
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Признаки параллельности двух прямых.Стр 1 из 3Следующая ⇒ Ответы на билеты по геометрии 7кпасс Билет 1 Точка, прямая, отрезок, луч, угол Часть прямой, ограниченная двумя точками, называется отрезком. Луч Точка, которая лежит на прямой, разделяет ее на две части, каждая из которых называется лучом, исходящим из этой точки. Точка - начало луча.
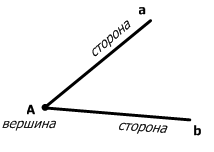
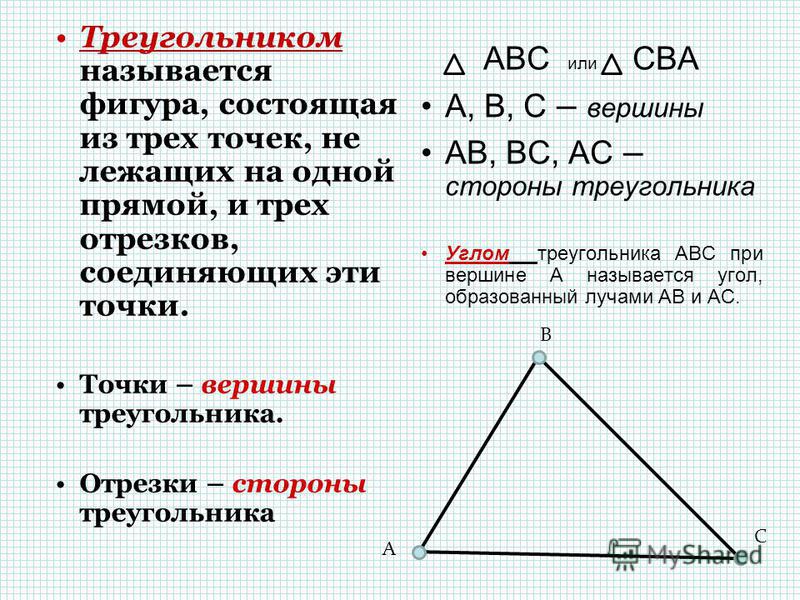
Угол - это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало - вершиной угла.
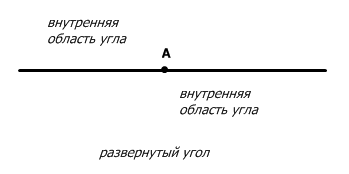
Угол называется развернутым, если обе его стороны лежат на одной прямой. В этом случае любая область плоскости является внутренней областью угла. Способы обозначения углов Одной заглавной латинской буквой, указывающей его вершину.
Тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.Угол: Двумя строчными латинскими буквами. Угол: 2.Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
AB=A1B1, AC=A1C1, ∠A=∠A1. ΔABC= ΔA1B1C1
Доказательство: Так как ∠A=∠A1, то можно треугольник A1B1C1 наложить на треугольник ABC так, чтобы · точка A1 совместилась с точкой A, · луч A1C1 наложился на луч AC, · луч A1B1 — на луч AB. Так как AB=A1B1, то при таком наложении сторона A1B1 совместится со стороной AB, а значит, точка B1 совместится с точкой B. Аналогично, сторона A1C1 совместится со стороной AC, а точка C1 — с точкой C.  Следовательно, сторона B1C1 совместится со стороной BC.Значит, при наложении треугольники полностью совместятся, поэтому ΔABC= ΔA1B1C1 (по определению). Билет 2 1. 2. Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника то такие треугольники равны.
ΔABC, . ΔABC= ΔA1B1C1 ΔA1B1C1, AB=A1B1, ∠A=∠A1, ∠B=∠B1 Доказательство: Так как AB=A1B1, то треугольник A1B1C1 можно наложить на треугольник ABC так, чтобы · сторона A1B1 совместилась со стороной AB, · точки C1 и С лежали по одну сторону от прямой AB. Поскольку ∠A=∠A1, сторона A1С1 при этом наложится на луч AC. Так как ∠B=∠B1, сторона B1C1 наложится на сторону BC. Точка С1 принадлежит как стороне A1С1, так и стороне B1C1, поэтому С1лежит и на луче AC, и на луче CB. Лучи AC и CB пересекаются в точке C. Следовательно, точка С1 совместится с точкой C. Значит, сторона A1С1 совместится со стороной AC, а сторона B1C1 — со стороной BC. Таким образом, при наложении треугольники ABC и A1B1C1 полностью совместятся. А это означает, что ΔABC= ΔA1B1C1 (по определению). Билет 3
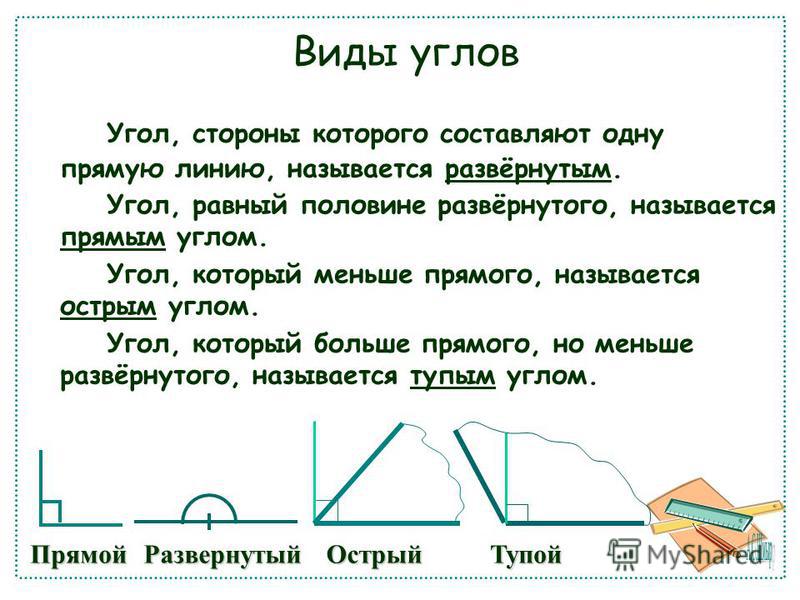
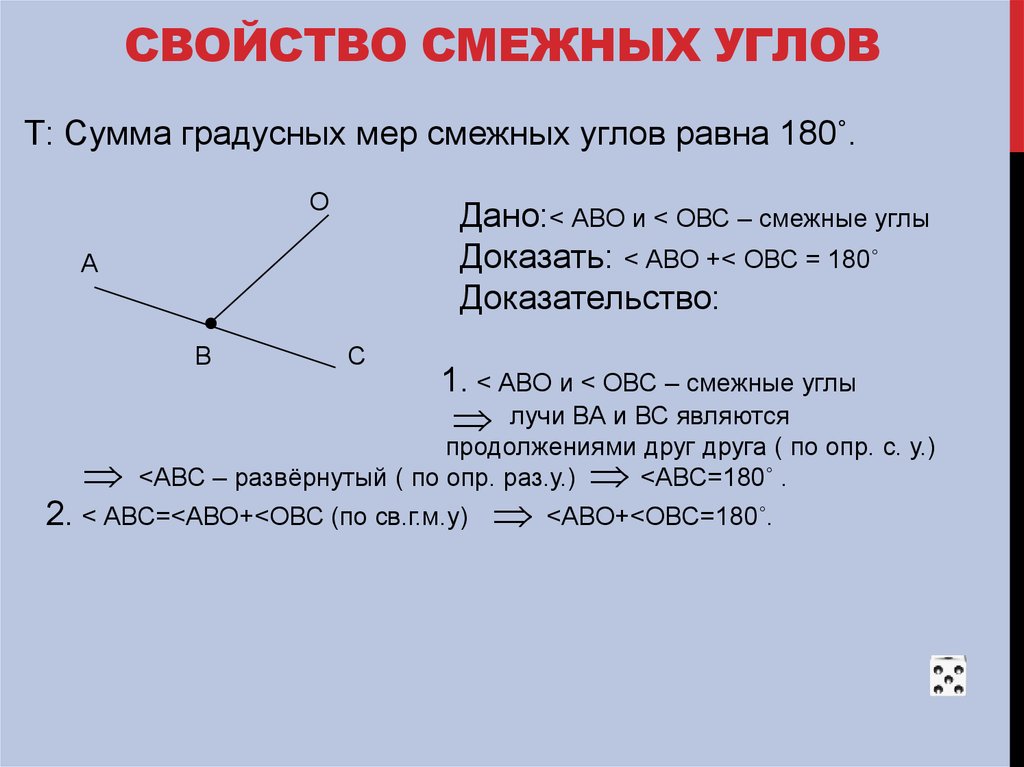
Два смежных углы образуют развернутый угол. Если два угла равны, то смежные с ними углы тоже равны. Угол, смежный с прямым углом, является прямым. Угол, смежный с острым углом, тупой. Угол, смежный с тупым углом, является острым. Любой луч, исходящий из вершины развернутого угла и проходящий между сторонами разделяет его на два смежные углы. Если два угла равны, то смежные с ними углы также равны. Два угла, смежные с одним и тем же углом, равны. Если два смежных углы равны, то они прямые.
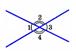
Билет 4 1. Определение. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. На рисунке углы 1 и 3, а также 2 и 4 – вертикальные. Вертикальные углы обладают следующим свойством. Свойство.Вертикальныеуглы равны. 2.
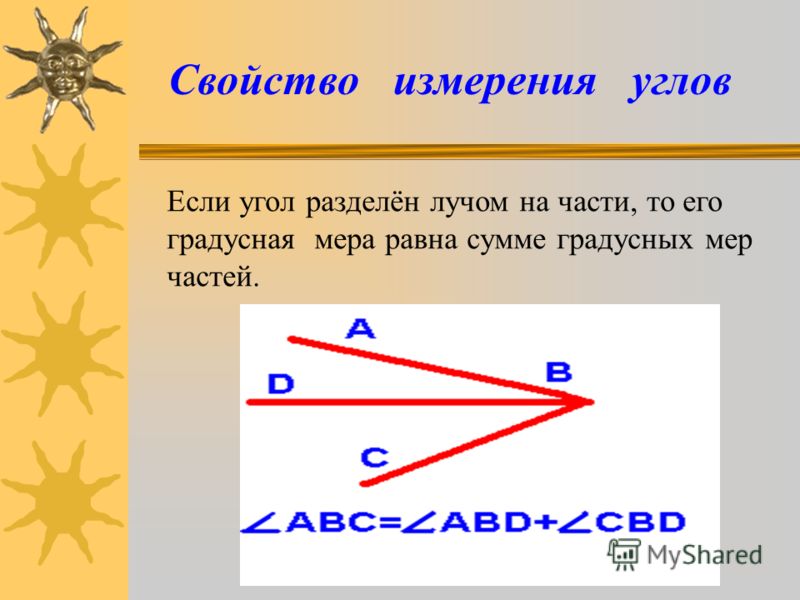
Билет5 1.Градусной мерой угла называется положительное число, которое показывает, сколько раз градус и его части - минута и секунда - укладываются в данном угле, то есть градусная мера - величина, отражающая количество градусов, минут и секунд между сторонами угла. Градус (от лат. gradus - деление шкалы, шаг, ступень) - единица измерения плоских углов в геометрии. Обозначается - 2.
2.
Билет 6 1. Периметром треугольника называется сумма всех его сторон Р = АВ + ВС = АС 2.
Билет 7 1. Равнобедренный треугольник, его свойства и признаки.
2.
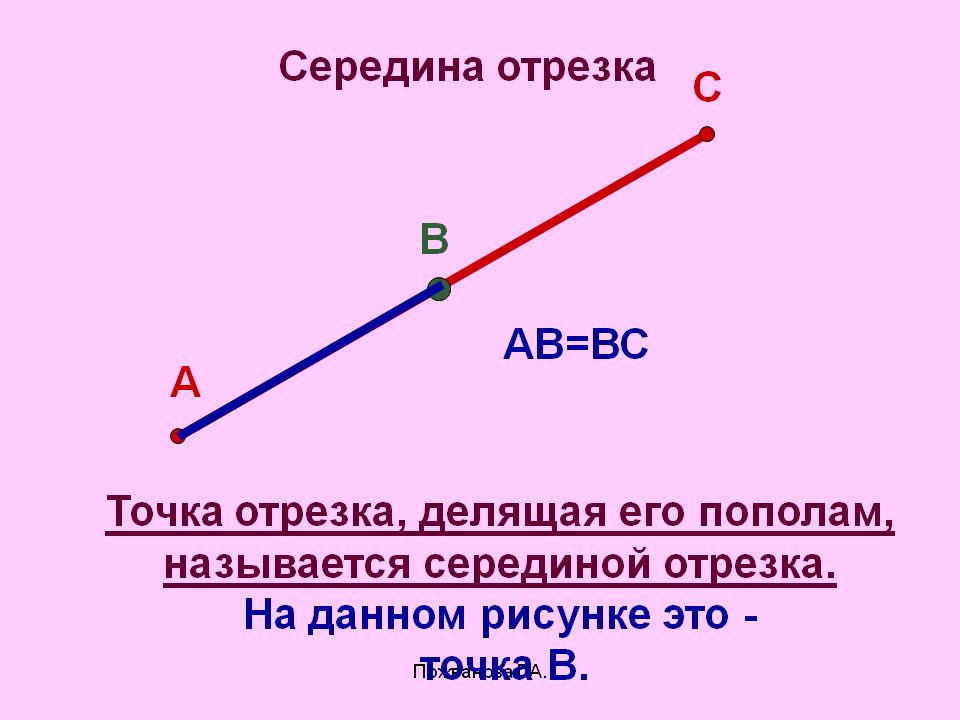
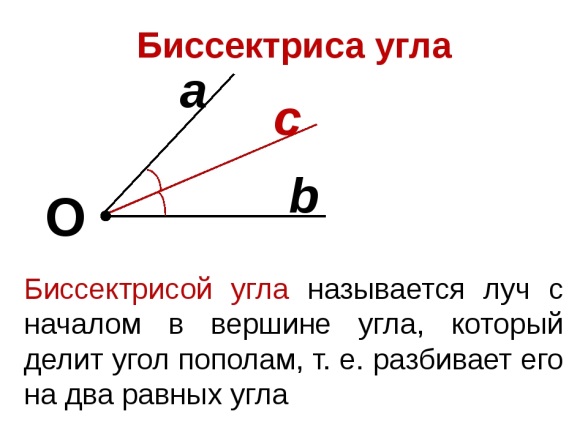
Билет 8 1. Медиана, биссектриса и высота треугольника.
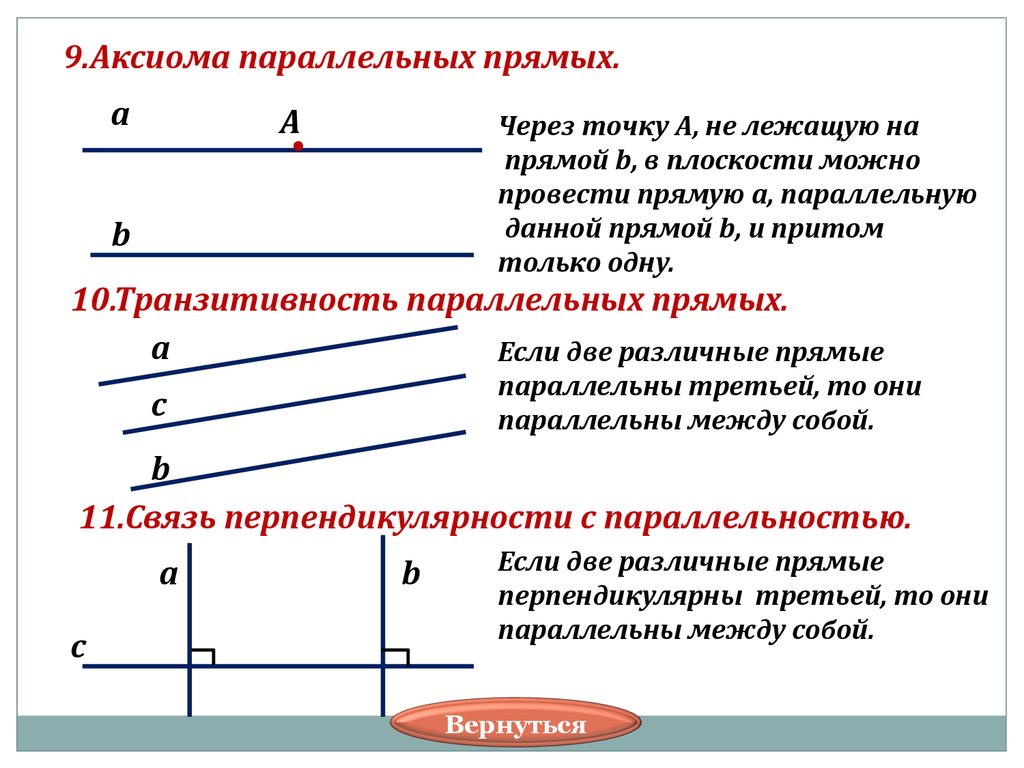
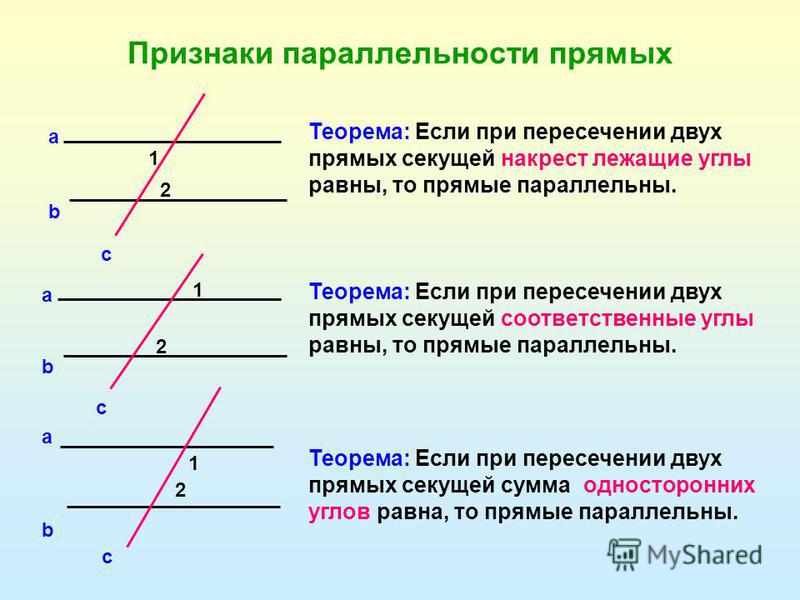
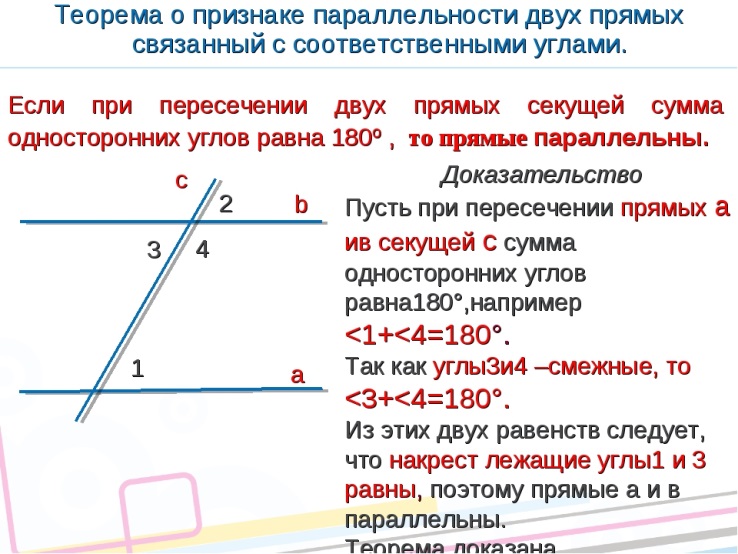
Признаки параллельности двух прямых.
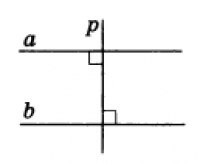
Следствие 1. Две различные прямые на плоскости, перпендикулярные одной и той же прямой, параллельны
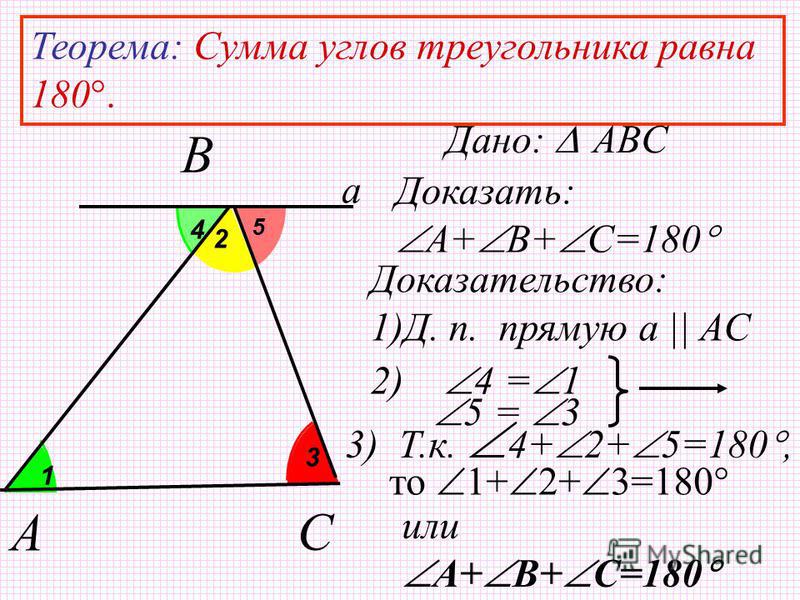
Билет 9 1. Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине. Как построить внешний угол треугольника? Нужно продлить сторону треугольника. ∠2 — внешний угол при вершине С, ∠1 — внешний угол при вершине В. При каждой вершине треугольника есть два внешних угла. Внешние углы каждой пары при данной вершины равны между собой Теорема (о внешнем угле треугольника) |
|||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 1967. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
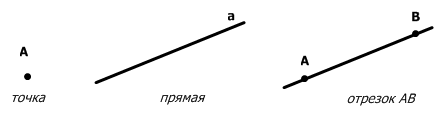 Отрезки, прямые и лучи обозначаются или одной малой или двумя заглавными латинскими буквами
Отрезки, прямые и лучи обозначаются или одной малой или двумя заглавными латинскими буквами
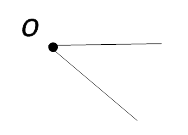 Угол:
Угол:  O
O 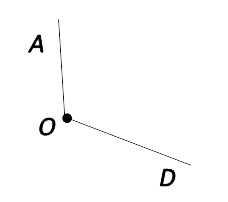 Угол:
Угол: 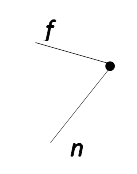
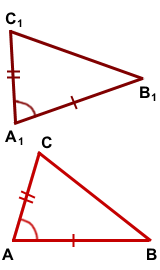 Дано: ΔABC, ΔA1B1C1, Доказать:
Дано: ΔABC, ΔA1B1C1, Доказать:
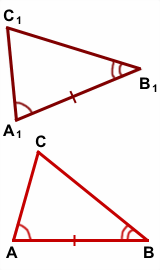 Дано: Доказать:
Дано: Доказать: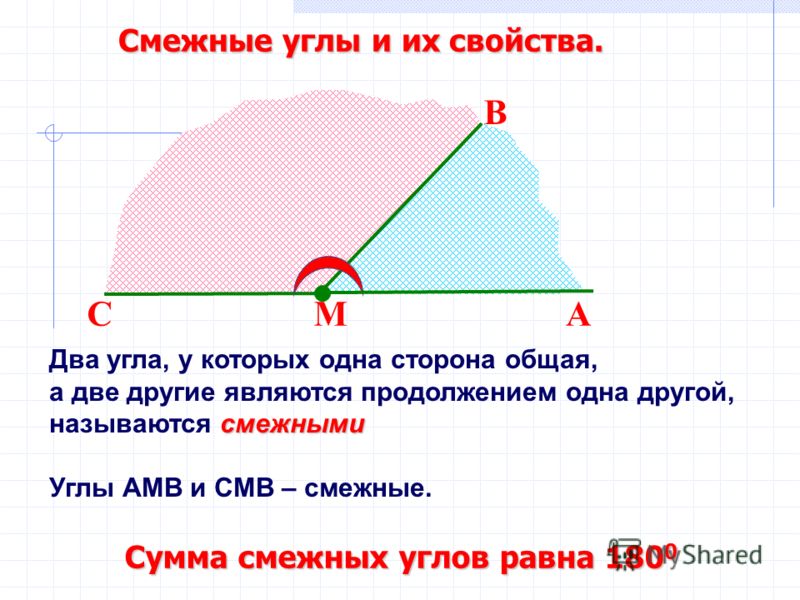 Сумма смежных углов равна 180 градусам.
Сумма смежных углов равна 180 градусам.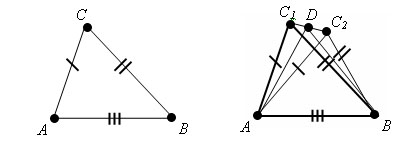 Дано: АВ = А1В1, В1С1=ВС АС=А1С1
Доказательство. Доказать: трАВС = трА1В1С1 Пусть треугольники ABC и A1B1C1 такие, что AB=A1B1, AC=A1C1, BC=B1C1. Требуется доказать, что треугольники равны. Допустим, что треугольники не равны. Тогда ∠ A ≠∠ A1, ∠ B ≠∠ B1, ∠ C ≠∠ C1 одновременно. Иначетреугольникибылибыравныпопервомупризнаку. Пусть треугольник A1B1C2 – треугольник, равный треугольнику ABC, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой A1B1. Пусть D – середина отрезка С1С2. треугольники A1C1C2 и B1C1C2 равнобедренные с общим основанием С1С2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой С1С2. Прямые A1D и B1D не совпадают, так как точки A1, B1, D не лежат на одной прямой. Но через точку D прямой С1С2 можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию. Теорема доказана.
Дано: АВ = А1В1, В1С1=ВС АС=А1С1
Доказательство. Доказать: трАВС = трА1В1С1 Пусть треугольники ABC и A1B1C1 такие, что AB=A1B1, AC=A1C1, BC=B1C1. Требуется доказать, что треугольники равны. Допустим, что треугольники не равны. Тогда ∠ A ≠∠ A1, ∠ B ≠∠ B1, ∠ C ≠∠ C1 одновременно. Иначетреугольникибылибыравныпопервомупризнаку. Пусть треугольник A1B1C2 – треугольник, равный треугольнику ABC, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой A1B1. Пусть D – середина отрезка С1С2. треугольники A1C1C2 и B1C1C2 равнобедренные с общим основанием С1С2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой С1С2. Прямые A1D и B1D не совпадают, так как точки A1, B1, D не лежат на одной прямой. Но через точку D прямой С1С2 можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию. Теорема доказана.
 .
.

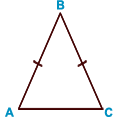 Равнобедренный треуг
Равнобедренный треуг 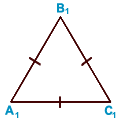 ольник — треугольник у которого равны две стороны. AB = BC — боковые стороны; AC — основание равнобедренного треугольника. Равносторонний треугольник — треугольник у которого все стороны равны. A 1B 1 = B 1C 1 = A 1C 1 — стороны треугольника.
Всякий равносторонний треугольник является равнобедренным, но не всякий равнобедренный — равносторонним.
ольник — треугольник у которого равны две стороны. AB = BC — боковые стороны; AC — основание равнобедренного треугольника. Равносторонний треугольник — треугольник у которого все стороны равны. A 1B 1 = B 1C 1 = A 1C 1 — стороны треугольника.
Всякий равносторонний треугольник является равнобедренным, но не всякий равнобедренный — равносторонним.
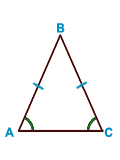
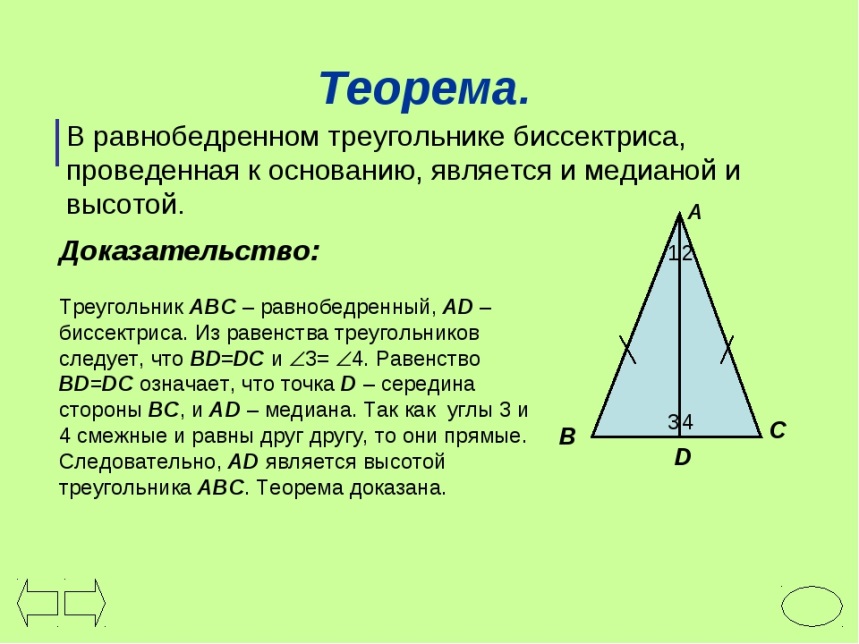
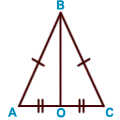 в равнобе
в равнобе 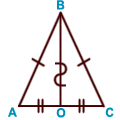 дренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;
• в равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой; • в равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
дренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;
• в равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой; • в равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.

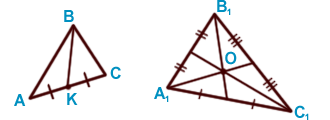 AK = KC , BK — медиана
AK = KC , BK — медиана  ABC , О — центр
ABC , О — центр 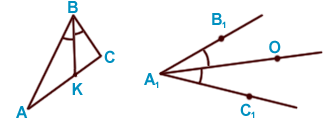
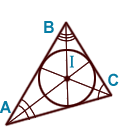 BK — биссектриса
BK — биссектриса 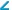 C 1A 1B 1 .
В каждом треугольнике можно провести 3 биссектрисы, которые пересекаются в одной точке, обычно обозначаемой латинской буквой I .
C 1A 1B 1 .
В каждом треугольнике можно провести 3 биссектрисы, которые пересекаются в одной точке, обычно обозначаемой латинской буквой I .
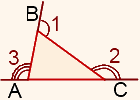 На рисунке:∠3 — внешний угол при вершине А,
На рисунке:∠3 — внешний угол при вершине А,