
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тема. МОДЕЛИ УПРАВЛЕНИЯ ЗАПАСАМИ ⇐ ПредыдущаяСтр 2 из 2 Управление запасами – важная часть общей политики управления оборотными активами предприятия, основная цель которой − обеспечение бесперебойного процесса производства и реализации продукции при минимизации совокупных затрат по обслуживанию запасов. Задача управления запасами состоит в определении размера и периодичности заказов, при которых издержки (функция суммарных затрат) принимают минимальное значение. Основная модель управления запасами (модель простейшего типа) характеризуется постоянным и непрерывным во времени спросом, мгновенным пополнением запаса и отсутствием дефицита, весь спрос удовлетворяется полностью. Под Q будем понимать весь запас материальных ресурсов (товаров) одного вида, израсходованный за плановый период времени T. Интенсивность спроса (в единицу времени) равна
График изменения запасов
Известные параметры модели управления запасами
Требуется определить размер заказываемой партии  Для нахождения минимума функции оптимальное число поставок за плановый период времени где ТЕМА. Статистические игры Пусть известны вероятности В случае, когда вероятности состояний природы правдоподобны, для их оценки используют принцип недостаточного основания Лапласа, согласно которому оптимальной считают стратегию Если вероятности состояний природы неизвестны, то для решения статистических игр – выбора оптимальной стратегии статистика – можно использовать несколько критериев. 1. Максминный критерий Вальда. По этому критерию рекомендуется применять максиминную стратегию. Она достигается из условия 2. Критерий максимума. Оптимальная стратегия выбирается из условия 3. Критерий Гурвица. Критерий рекомендует стратегию, определяемую по формуле 4. Критерий Сэвиджа. Согласно этому критерию, рекомендуется выбирать ту стратегию, при которой в наихудших условиях величина риска принимает наименьшее значение:
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 208. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ед., причем
ед., причем  . В момент, когда запас достигнет нуля, поступает заказ, равный
. В момент, когда запас достигнет нуля, поступает заказ, равный  ед., и уровень запаса восстанавливается до максимального значения. Средний уровень запасов −
ед., и уровень запаса восстанавливается до максимального значения. Средний уровень запасов − 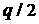 . Продолжительность цикла расходования запаса от максимального значения
. Продолжительность цикла расходования запаса от максимального значения  единиц времени.
единиц времени. 


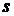
 и интервал времени между поставками
и интервал времени между поставками  таким образом, чтобы общие затраты, связанные с организацией заказов и хранением товаров, были минимальными. Суммарные затраты в единицу времени, связанные с организацией заказов и хранением товаров, можно представить в виде:
таким образом, чтобы общие затраты, связанные с организацией заказов и хранением товаров, были минимальными. Суммарные затраты в единицу времени, связанные с организацией заказов и хранением товаров, можно представить в виде:  , где
, где  − затраты на оформление заказа в ед. времени,
− затраты на оформление заказа в ед. времени,  − затраты на хранение запасов в ед. времени. Отметим, что здесь мы не учитываем стоимость товара и потери от дефицита.
− затраты на хранение запасов в ед. времени. Отметим, что здесь мы не учитываем стоимость товара и потери от дефицита. приравняем к нулю ее производную. Тогда оптимальный размер заказаи оптимальный интервал между поставками определяются по формулам
приравняем к нулю ее производную. Тогда оптимальный размер заказаи оптимальный интервал между поставками определяются по формулам  ,
,  . При этом минимальные суммарные затраты в единицу времени −
. При этом минимальные суммарные затраты в единицу времени −  ; оптимальный средний уровень текущего запаса −
; оптимальный средний уровень текущего запаса −  ;
;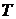 −
−  или
или  ,
,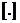 − целая часть числа; относительное изменение суммарных затрат по сравнению с оптимальным значением при относительном изменении объема партии−
− целая часть числа; относительное изменение суммарных затрат по сравнению с оптимальным значением при относительном изменении объема партии−  .
. состояний
состояний  природы. По критерию Байеса оптимальной считается чистая стратегия
природы. По критерию Байеса оптимальной считается чистая стратегия  , при которой максимизируется средний выигрыш
, при которой максимизируется средний выигрыш 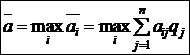 или минимизируется средний риск
или минимизируется средний риск  .
.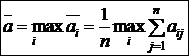 .
. ,
,  ,
, ,
,  ,
, 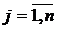 .
.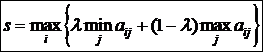 ,
,  (степень оптимизма) изменяется в диапазоне [0,1].
(степень оптимизма) изменяется в диапазоне [0,1]. – оптимальная стратегия, где
– оптимальная стратегия, где  - элементы матрицы рисков.
- элементы матрицы рисков.