
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тема. Элементы корреляционно-регрессионного анализаСтр 1 из 2Следующая ⇒ А Парная регрессия. Теоретическая линейная регрессионная модель имеет вид:
где X – неслучайная (детерминированная) величина, а Y,
где Для конкретного наблюдения
Оценка параметров
Выборочный коэффициент регрессии Для оценки влияния фактора x на результативный признак y применяется коэффициент эластичности Тесноту линейной связи изучаемых явлений оценивает коэффициент парной корреляции
где
 Чем ближе
Если Проверка общего качества уравнения регрессии – соответствие уравнения регрессии статистическим данным. Суммарной мерой качества уравнения регрессии является коэффициент детерминации БМножественная регрессия. Уравнение множественной эмпирической линейной регрессии имеет вид: Коэффициенты Коэффициенты парной корреляции Если Качественные характеристики связи
Множественная корреляция возникает от взаимодействия нескольких факторов с результативным показателем. В общем случае коэффициент детерминации рассчитывается по формуле: Для проверки адекватности модели используется F-статистика (критерий Фишера)
Если при заданном уровне значимости |
|||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 189. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
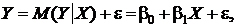
 − случайные величины. Y называется объясняемой (зависимой) переменной, а
− случайные величины. Y называется объясняемой (зависимой) переменной, а  – объясняющей (независимой) переменной (фактором) или регрессором. Оценкой теоретической функции регрессии по выборке
– объясняющей (независимой) переменной (фактором) или регрессором. Оценкой теоретической функции регрессии по выборке 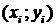 ,
,  , ограниченного объема n является эмпирическое (выборочное) уравнение регрессии:
, ограниченного объема n является эмпирическое (выборочное) уравнение регрессии:
 – оценка условного математического ожидания
– оценка условного математического ожидания  ;
;  и
и  – оценки неизвестных параметров
– оценки неизвестных параметров 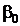 и
и 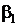 , называемые выборочными коэффициентами регрессии.
, называемые выборочными коэффициентами регрессии. , где остаток регрессии
, где остаток регрессии  − оценка теоретического случайного отклонения
− оценка теоретического случайного отклонения  .
.
 и
и  уравнения (1) осуществляется методом наименьших квадратов.Система нормальных уравнений для определения параметров линейной парной регрессии МНК имеет вид:
уравнения (1) осуществляется методом наименьших квадратов.Система нормальных уравнений для определения параметров линейной парной регрессии МНК имеет вид: 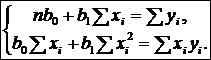 Решения системы
Решения системы  где
где  − выборочные средние значения переменных.
− выборочные средние значения переменных. или
или 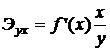 . Он показывает, на сколько процентов в среднем изменяется результативный признак y при изменении факторного признака x на 1%.
. Он показывает, на сколько процентов в среднем изменяется результативный признак y при изменении факторного признака x на 1%. :
: ,
, ,
,  – средние значения независимой и зависимой переменной;
– средние значения независимой и зависимой переменной; ,
,  — средние квадратические отклонения случайных величин X и Y
— средние квадратические отклонения случайных величин X и Y ,
, 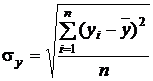 .
. к единице, тем теснее связь. При
к единице, тем теснее связь. При 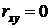 линейная корреляционная связь отсутствует. Для проверки значимости коэффициента корреляции используется t-критерий Стьюдента:
линейная корреляционная связь отсутствует. Для проверки значимости коэффициента корреляции используется t-критерий Стьюдента: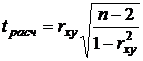 .
.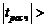
 , то значение коэффициента корреляции признается значимым, в противном случае – незначимым (
, то значение коэффициента корреляции признается значимым, в противном случае – незначимым ( 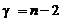 ).
). . В случае парной линейной регрессии коэффициент детерминации равен квадрату коэффициента корреляции:
. В случае парной линейной регрессии коэффициент детерминации равен квадрату коэффициента корреляции: 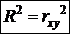 . Величина
. Величина  для регрессии (1). Чем ближе
для регрессии (1). Чем ближе 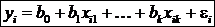 , где
, где 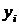 – i-е наблюдение зависимой переменной,
– i-е наблюдение зависимой переменной, 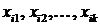 – i-е наблюдения независимых переменных
– i-е наблюдения независимых переменных  ,
,  – количество наблюдений (объем выборки);
– количество наблюдений (объем выборки);  – количество независимых переменных в уравнении.
– количество независимых переменных в уравнении.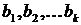 показывают количественное воздействие каждого фактора на результативный показатель при неизменности значений других факторов. Коэффициенты эластичности
показывают количественное воздействие каждого фактора на результативный показатель при неизменности значений других факторов. Коэффициенты эластичности  показывают, на сколько процентов в среднем изменяется функция с изменением аргумента на 1%.
показывают, на сколько процентов в среднем изменяется функция с изменением аргумента на 1%. ,
, 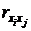 используются в качестве меры, характеризующей степень линейной связи двух переменных. Коэффициент корреляции принимает значение от -1 до +1. Если
используются в качестве меры, характеризующей степень линейной связи двух переменных. Коэффициент корреляции принимает значение от -1 до +1. Если 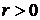 , то корреляционная связь между переменными является прямой, если
, то корреляционная связь между переменными является прямой, если  – обратной.
– обратной. , корреляционная связь представляется линейной функциональной зависимостью. При
, корреляционная связь представляется линейной функциональной зависимостью. При  =0 линейная корреляционная связь отсутствует.
=0 линейная корреляционная связь отсутствует.



 .
. .
. расчетное значение критерия
расчетное значение критерия  больше табличного
больше табличного  , где степени свободы
, где степени свободы  ,
,  то модель считается значимой, гипотеза о случайной природе оцениваемых характеристик отклоняется, признается их статистическая значимость.
то модель считается значимой, гипотеза о случайной природе оцениваемых характеристик отклоняется, признается их статистическая значимость.