Методические указания к выполнению курсовой работы на примере моделирования электрической схемы

Методические указания к выполнению курсовой работы

По курсу «Объектно-ориентированное программирование»

Требования к выполнению курсовых заданий

В задании описана некоторая предметная область (ПрО), все процессы в которой развиваются во времени. Следует разработать программу в объектно-ориентированной парадигме, которая смоделирует на задаваемом пользователем интервале времени Т в ускоренном режиме с масштабом времени 1:М (1 ед. времени работы программы соответствует М ед. времени функционирования моделируемой ПрО) ее жизненный цикл.

Требуется:

1.Разработать информационную модель заданной предметной области.

2.На основе информационной модели разработать модель состояний (если она будет выбрана для реализации).

3.Разработать класс «МОДЕЛЬ», который находится с классами предметной области в отношении «часть» той или иной кратности, или включает граф состояний объектов предметной области.

4.Разработать класс «ДВИЖОК», объект которого, взаимодействуя с объектом класса «МОДЕЛЬ», организует процесс моделирования во времени жизненного цикла объектов предметной области.

5.Разработать класс «СТАТИСТИК», объект которого вычисляет среднее значение и среднеквадратичное отклонение выбранной характеристики, как случайного процесса, какого-либо параметра предметной области (выбор осуществляется самостоятельно) на интервале  моделирования Т.

6.Общий интерфейс программы должен включать меню команд, позволяющих в произвольные моменты работы программы:

- вызывать окно, для просмотра и корректировки заданных параметров ПрО,

- вызывать окно отображения (в мнемонической, текстовой или графической форме) динамики изменения состояний объектов ПрО,

- запускать/останавливать/приостанавливать работу «ДВИЖКА», а также устанавливать время Т и масштаб времени М моделирования,

- вызывать окно отображения текущих вычисляемых характеристик вычисляемых объектом класса «СТАТИСТИК»,

- вызывать окно (только в режиме останова моделирования) тестирования датчика случайных чисел, в котором для задаваемой длины выборки N по кнопке запуска теста вычисляются и выводятся оценки математического ожидания и среднеквадратичного отклонения.

7.Значения, указанные в заданиях символьными обозначениями, в программе должны быть заданы по умолчанию конкретными величинами.

Требования к оформлению курсовых заданий

1. В каждой группе задания выбираются индивидуально и различными.

2. Пояснительная записка должна содержать:

- задание, в котором выделены предметы и/или понятия, составляющие объектную модель ПрО,

- граф отношений классов разработанных или взятых из используемой библиотеки классов. Желательно представлять граф в виде подграфов реализации «ПРИЛОЖЕНИЯ», «ИНТЕРФЕЙСА», «ДВИЖКА», «МОДЕЛИ» ПрО, «СТАТИСТИКА» и вспомогательных классов, в частности «ДАТЧИК СЧ».

Для модели ПрО:

- перечень событий, возникающих в ПрО, следствием которых является изменение свойств объектов ПрО,

- при использовании для реализации модели состояний ПрО: анализ возможных состояний и ориентированный (дуга из нач. состояния в конечное состояние) и раскрашенный (дуге поставлено в соответствие событие, инициирующее переход) граф перехода состояний модели ПрО,

- заголовочные файлы описания классов предметной области с комментариями, обосновывающими перечень выделенных свойств и реализованных методов,

- таблицу значений параметров модели по умолчанию,

- скриншоты экранов, демонстрирующие реализованный интерфейс программы,

- выводы по выполненному курсовому проекту.

Рекомендуемая среда реализации курсовой работы Qt Creator, для реализации проектов в которой используется библиотека классов Qt.

Электронную копию отчета, демонстрационный файл и все исходные тексты программы отправлять на почтовый адрес ssegorov@bk.ru.

Задание 1

На автозаправочной станции установлено 2 колонки, каждая из которых заправляет с двух сторон одним видом топлива. Если заправка невозможна, то автомобили становятся в очередь. Площадка при АЗС допускает пребывание в очереди на заправку не более трех автомобилей одновременно. Если в очереди уже находится три автомобиля, то очередной автомобиль, прибывший к станции, в очередь не становится, а проезжает мимо. Поток автомобилей, прибывающих для заправки, имеет интенсивность Z автомобилей в минуту. С вероятностью P ему требуется первый вид топлива, а 1-P – второй, в количестве Q литров, равномерно распределенном на интервале (Q1,Q2). Процесс заправки продолжается в среднем V литров в мин. Все потоки простейшие.

Задание 2

Пост диагностики автомобилей проводит диагностику двух видов, каждый на своем единственном комплекте оборудования. Заявка на диагностику, поступившая в момент, когда необходимое оборудование занято, получает отказ. Интенсивность потока заявок на диагностику равна Z автомобиля в час, причем с вероятностью P1 автомобилю требуется диагностика только первого вида, P2 – второго и 1-P1-P2 - обоих. Порядок прохождения диагностики двух видов не важен. Средняя продолжительность диагностик R1 и R2 часа соответственно. Все потоки событий в системе простейшие.

Задание 3

В инструментальном отделении сборочного цеха работают три кладовщика. В среднем рабочие приходят за инструментом раз в T мин. Обслуживание одного рабочего занимает у кладовщика R мин. Очередь ограничена величиной N. Известно, что поток рабочих за инструментом - простейший, а время обслуживания подчинено экспоненциальному закону распределения.

Задание 4

Билетная касса работает без перерыва. Билеты продают два кассира. Среднее время обслуживания кассирами R1 и R2 мин. соответственно на каждого человека. Пассажиры становятся в ту очередь, но не более 3 человек, которая меньше, а при равных условиях в первую кассу. Среднее число пассажиров, желающих приобрести билеты в кассе в течение одного часа, равно Z пасс/час. Все потоки в системе простейшие.

Задание 5

Малое транспортное предприятие эксплуатирует 4 автомобиля, 2 грузовых и 2 легковых. Простейший поток отказов каждого автомобиля имеет интенсивность Z₁ и Z₂ отказов в день соответственно для грузовых и легковых автомобилей. На предприятии работают 3 механика, из них только один может обслуживать и грузовые и легковые автомобили. Среднее время устранения одного отказа грузового автомобиля равно R₁ часов, а легкового – R₂ часов. Все потоки событий простейшие.

Задание 6

Технические устройства (ТУ) в количестве 3 ед. могут время от времени выходить из строя (отказывают). Поток отказов для каждого ТУ простейший с интенсивностью равной Z отказов в сутки. Время восстановления ТУ имеет экспоненциальное распределение. Математическое ожидание времени обслуживания - R суток. Количество каналов, выполняющих обслуживание ТУ, равно 2 ед. Количество заявок в очереди ограничено значением 2.

Задание 7

В парикмахерскую, в которой работают мастер и ученик, приходят клиенты в среднем с интервалом Tминут. Пришедший

клиент направляется к мастеру, если он свободен, и к ученику, в противном случае. Когда мастер и ученик заняты, клиент располагается в зале, где имеются два стула для ожидающих клиентов. Если оба стула заняты, то пришедший клиент покидает парикмахерскую. Мастер работает в K раз быстрей, чем ученик, и тратит на обслуживание в среднем R минут. Все потоки событий простейшие.

Задание 8

Система массового обслуживания - билетная касса с тремя окошками (с тремя кассирами) и очередью длины 2. Пассажиров, желающих купить билет, приходит в среднем N человек за T мин. Поток пассажиров можно считать простейшим. Они выбирают кассу с вероятностями P1, P2, P3. Кассиры в среднем обслуживает M пассажиров за R1, R2 и R3 мин. соответственно. Время обслуживания подчинено экспоненциальному закону распределения.

Задание 9

На автозаправочной станции (АЗС) имеется две колонки: одна для заправки легковых автомобилей бензином и другая для заправки грузовых автомобилей дизельным топливом. На станцию прибывают автомобили со средним интервалом между моментами прибытия Tминут, причем легковые автомобили прибывают в K раз чаще, чем грузовые. Время заправки легковых автомобилей в среднем составляет Rминут, а грузовых – в M раз больше. Перед АЗС имеется площадка для ожидания прибывающих автомобилей, на которой могут разместиться один грузовой или два легковых автомобиля. Если площадка занята, то автомобили покидают АЗС.

Задание 10

В автомобильной мастерской работает один мастер. Средний интервал между моментами поступления автомобилей в мастерскую составляет T минут. Каждый автомобиль необходимо сначала помыть, а затем выполнить технический осмотр. Мастер тратит на каждую из этих операций случайное время со средним значением R1и R2минут соответственно. Если мастер занят, то очередной прибывший автомобиль с вероятностью P остается и ожидает обслуживания. Если при этом мойка свободна, то он заезжает на мойку и ожидает там. Если мойка занята, а в мастерской уже имеется автомобиль, ожидающий обслуживания, то очередной прибывший автомобиль покидает мастерскую не обслуженным.

Задание 11

На промышленном предприятии в ремонтном цехе работают N механиков. Предприятие имеет M станков с учетом числа находящихся в ремонте. Отказы станков происходят с частотой Z отказов в час. Для устранения неисправности станка одному механику требуется в среднем R мин. Распределение моментов возникновения отказов станков является экспоненциальному, продолжительность выполнения ремонтных работ также подчинена экспоненциальному закону.

Задание 12

В вычислительном центре работает 3 персональных компьютера (ПК). Простейший поток неисправностей имеет интенсивность Z отказов в день. ПК отказывают с одинаковой вероятностью, причем неисправный ПК отказать не может. Неисправность проявляется в момент ее возникновения, но для определения ПК с неисправностью свободный инженер должен случайным образом обходить работающие ПК, исключая те, которые уже находятся в ремонте. Среднее время определения неисправности на ПК равно D час. Среднее время устранения одной неисправности одним инженером равно R час. Компьютеры обслуживают три инженера. Все потоки событий - простейшие.

Задание 13

На станции технического обслуживания (СТО) автомобилей работают два человека: мойщик автомобилей и мастер по техническому обслуживанию (ТО). В течение дня на станцию прибывают автомобили, средний интервал между моментами поступления автомобилей в мастерскую составляет T минут, причем D% прибывающих автомобилей сначала необходимо помыть, а затем выполнить ТО, остальным автомобилям требуется только ТО. Если мойщик занят, то прибывший на мойку автомобиль остается и ожидает обслуживания при условии, что нет других ожидающих мойки автомобилей, в противном случае автомобиль покидает станцию. Прошедший мойку автомобиль не уезжает со СТО и направляется на ТО вне очереди. Если мастер по ТО занят, то автомобиль, не нуждавшийся в мойке, остается и ожидает обслуживания при условии, что нет ожидающих ТО автомобилей, в противном случае автомобиль покидает станцию.

Задание 14

В вычислительном центре работает 5 персональных компьютеров (ПК). Простейший поток задач (заявки), поступающих на ВЦ, имеет интенсивность в Z задач в час. Интенсивность сбоя любого ПК равна S сбоев в час. Задача, решаемая в момент сбоя, получает отказ. Среднее время решения задачи равно R мин. Заявка получает отказ, если все ПК заняты.

Задание 15

На пункт техосмотра поступает простейший поток заявок (автомобилей) интенсивности Z машин в час. Время осмотра распределено по экспоненциальному закону и равно в среднем R мин., в очереди может находиться не более N автомобилей. Автомобиль, если в очереди находится не менее N/2 автомобилей с вероятностью P уезжает.

Задание 16

На АЗС имеются 3 заправочные колонки. Заправка одной машины длится в среднем R мин., а обслуживание единственным кассиром – T мин. Колонка освобождается только после обслуживания водителя кассиром. В среднем на АЗС каждые Z минут прибывает машина, нуждающаяся в заправке бензином. Она встает на заправку или, если все колонки заняты, в очередь к определенной колонке. Выбор колонки равновероятен. Число мест в очереди ограничено значением 2. Все машины, вставшие в очередь на заправку, дожидаются своей очереди. Все потоки в системе простейшие.

Задание 17

В аудиторскую фирму поступает простейший поток заявок на обслуживание с интенсивностью Z заявок в день. Время обслуживания распределено по экспоненциальному закону и равно в среднем D дням независимо от того, кто выполняет обслуживание. Аудиторская фирма располагает пятью независимыми бухгалтерами, выполняющими аудиторские проверки (обслуживание заявок). Каждый бухгалтер имеет свой рейтинг, равный W_i, согласно которому вычисляется вероятность выбора на обслуживание из числа свободных. Очередь заявок ограничена значением 3.

Задание 18

В бухгалтерии предприятия имеются два кассира, каждый из которых может обслужить в среднем R сотрудников в час. Поток сотрудников, получающих заработную плату, - простейший, с интенсивностью, равной Z сотрудников в час. Очередь в кассе не более 3. Время обслуживания подчинено экспоненциальному закону распределения.

Задание 19

В магазине в трех отделах работают по одному продавцу, которые могут обслужить в час в среднем N покупателей. Поток покупателей простейший с интенсивностью, равной M покупателей в час. Каждому покупателю с вероятностями P1, P2 и P3 необходимо сделать покупки в соответствующих отделах, которые они обходят в порядке их нумерации. В очереди в каждый отдел может стоять не более 2 человек. Все потоки событий простейшие.

Задание 20

На железнодорожную станцию, имеющую две сортировочных горки, прибывают составы с интенсивностью Z составов в час. Среднее время, в течение которого горки обслуживают состав, равно R1 и R2 час. соответственно. Составы, прибывающие в момент, когда горка занята, становятся в очередь и ожидают в парке прибытия, где имеется три запасных пути, на каждом из которых может ожидать один состав. С первого запасного пути можно заехать только на первую горку, с третьего – только на вторую, а со второго на любую. Состав, прибывший в момент, когда все три запасных пути в парке прибытия заняты, проезжает мимо. Все потоки событий простейшие.

Задание 21

В мужской парикмахерской работают два мастера. Средний интервал между моментами прихода клиентов составляет Х минут. Каждый клиент с вероятностью P просит сначала побрить, а затем постричь, и 1-P – сразу подстричь. Мастера тратят на каждуюиз этих операций случайное время со средними значениями Y1 и Y2 минут соответственно. В парикмахерской к каждому мастеру имеется одно кресло для ожидания. Если оба кресла свободны, то их выбор равновероятен. Если кресла заняты, то очередной пришедший клиент уходит из парикмахерской не обслуженным.

Задание 22

На станцию технического обслуживания (СТО) автомобилей каждые T часов подъезжает в среднем одна машина. Станция имеет 4 поста обслуживания, расположенных в 2 боксах (по 2 поста на бокс). Очереди автомобилей, ожидающих обслуживания на постах, свои для каждого бокса ограничены значением 2. Выбор очереди производится равновероятно. Среднее время обслуживания одной машины на посту R часов. В процессе обслуживания с вероятностью P обнаружится еще одна неисправность, и машина обслуживается еще один сеанс на том же посту. Все потоки в системе простейшие.

Задание 23(Лифт)

В 3-х этажном доме в каждом из 2 подъездов работают по 1 лифту, каждый грузоподъемностью G кг. Интенсивности подхода пассажиров на первых этажах равна Z человек в час, а на верхних в N раз меньше. Вес подошедшего пассажира подчиняется равномерному закону распределения на интервале (G1,G2) кг. С первого этажа пассажирам требуется этажи с раной вероятностью. Пассажиры с верхних этажей едут только на первый. Пассажиры входят в лифт в порядке их прибытия. Лифт передвигается со скоростью V этажей в сек. Вызывается только свободный лифт. Лифт, едущий вверх, останавливается на этажах, которые затребовали едущие пассажиры и не загружается дополнительно. Лифт, едущий вниз, останавливается на промежуточных этажах и пополняется. Лифт не может быть перегружен.

Задание 24

Имеется набор элементов: батарейка напряжения V вольт,

Выключатель на 2 положения (вкл/выкл), лампочки номиналом V1 и V2 вольт, соединительные провода. Из элементов собирается последовательно-параллельная схема. Если напряжение на лампочке больше номинала, то она сразу сгорает, если не больше, то горит с накалом пропорциональным отношению напряжений и может перегореть через интервал, распределенный по экспоненциальному закону распределения со средним в T сек. Если батарейка закорочена, то она садится. Время замены неисправных элементов распределено по экспоненциальному закону распределения со средним в R сек.

Задание 25

   Имеется 8 абонентов телефонной сети, подключенных к АТС емкостью в N одновременных соединений. Каждый абонент имеет потребность позвонить другим с равной вероятностью и средним интервалом в Z минут. Он ожидает соединения со средним временем S сек. Соединение не устанавливается, если емкость соединений исчерпана, телефон вызываемого абонента занят или он не подошел за требуемое время. Среднее время ответа на вызов T сек. Средние времена разговора со стороны инициатора – R1 минут, со стороны ответчика – R2 минут.

Задание 26

   На перекрестке главной дороги с двумя полосами движения в обе стороны и второстепенной - с одной полосой движения в обе стороны установлены светофоры. Интенсивность подъезда к перекрестку автомобилей по главной дороге Z1 автомобилей в час по каждой полосе, по второстепенной – Z2. Автомобили проезжают перекресток только прямо, по зеленому сигналу светофора, не перестраиваясь в другую полосу, со средним временам R сек. Времена согласованных переключений светофоров заданы.

Методические указания к выполнению курсовой работы на примере моделирования электрической схемы

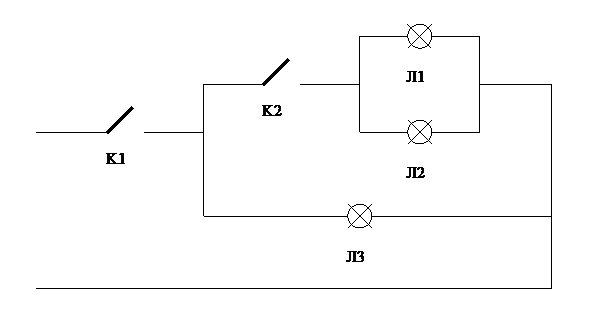
Задана схема, содержащая 2 выключателя (К1 и К2) и 3 лампочки (Л1, Л2 и Л3).

1. Выключатель К1 имеет начальное состояние «разомкнут» и переключается через равные промежутки времени Т1.

2. Выключатель К2 имеет начальное состояние «разомкнут» и переключается через случайные промежутки времени, распределенные по экспоненциальному закону распределения со средним значением Т2.

3. Лампочки в горящем состоянии могут перегорать. Интервал времени с момента включения лампочки до ее перегорания имеет равномерное распределение на интервале (L1 – L2). Время замены перегоревшей лампочки постоянное и равно L3.

Задание.

Смоделировать работу схемы на интервале времени (0 – Т), в качестве анализируемого параметра выбрать время непрерывного горения лампочки Л2.

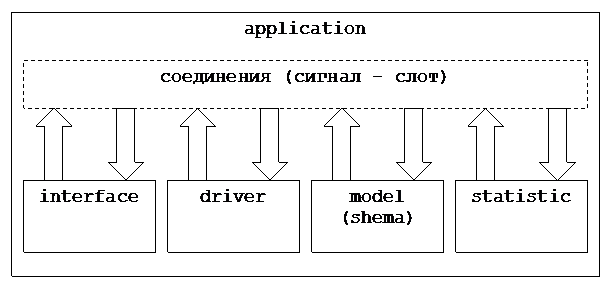
ПРИЛОЖЕНИЕ

Диаграмма отношений классов верхнего уровня.

Схема взаимодействия объектов верхнего уровня.

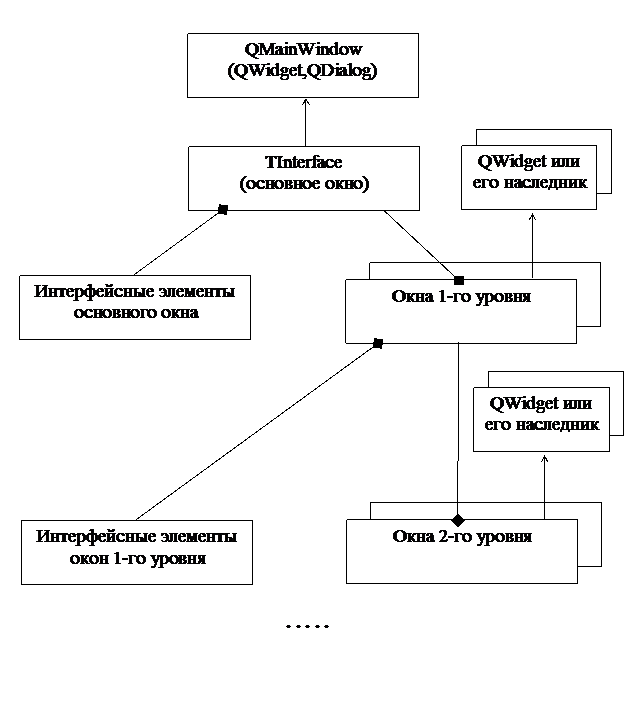
ИНТЕРФЕЙС

Диаграмма отношений классов реализации «ИНТЕРФЕЙСА»

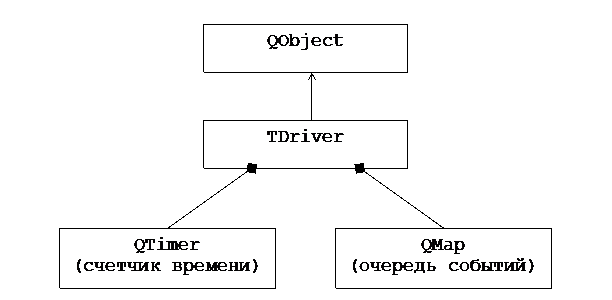
ДВИЖОК

Диаграмма отношений реализации класса TDriver

Алгоритм работы движка (в состоянии «работа»)

1. в исходном состоянии модельное время t₀ = 0. В очереди событий записано событие Е₀ («старт») со временем исполнения 0 - (0,E₀).

2. по каждому тику таймера с периодом Δt изменяется модельное время t_i+1 = t_i + Δt.

3. согласно модельному времени рассчитывается реальное время T_i+1 = M * t_i, где М – коэффициент пересчета модельного времени в реальное.

4. Излучаются сигналы с событиями, записанными в очередь событий с временами исполнения <= T_i+1, они удаляются из очереди.

5. При получении сигнала от модели с отложенным событием (t_e,E_k), где t_e - реальное время отложенного события E_k. Оно записывается в очередь событий, которая упорядочивается по времени (автоматически поддерживается объектом класса QMap).

Для взаимодействия «движка» и «модели» в классе TDriver описываются сигнал sendEvent и слот recieveEvent, обменивающимися 2-мя параметрами: double (планируемое время возникновения события) и TEvent (структура, определяющая понятие «событие»).

МОДЕЛЬ (индивидуальна для каждого варианта ПрО)

Диаграмма отношения классов реализации «МОДЕЛИ», построенная по информационной модели ПрО для решаемой задачи «Схема»

Диаграмма класса модель, построенная по модели состояний ПрО для решаемой задачи «Схема»