
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Неоднородные дифференциальные уравнения высших порядков. Общая методика их решения.Алгоритм решения неоднородного ДУ следующий: 1) Сначала нужно найти общее решение соответствующего однородного уравнения. Да-да, взять уравнение 2) Наиболее трудный этап. Необходимо найти какое-либо частное решение Внимание! Для освоения метода подбора будет жизненно необходим методический материал Как подобрать частное решение неоднородного уравнения? Данную справку лучше по возможности распечатать, очень удобно, если она будет перед глазами. Но не спешите вникать в эти таблицы, если являетесь чайником! Всему свое время. 3) На третьем этапе надо составить общее решение Если изначально в условии сформулирована задача Коши (найти частное решение, удовлетворяющее заданным начальным условиям), то добавляется четвёртый этап: 4) Нахождение частного решения, удовлетворяющего заданным начальным условиям. Порядок нахождения частного решение для уравнения второго порядка уже немного рассмотрен на уроке Однородные уравнения второго и высших порядков. В случае с неоднородным диффуром принципы нахождения частного решения сохраняются. Примечание: В ваших лекциях, практических занятиях общее решение однородного уравнения  Не так всё страшно, переходим к практическим задачам. Пример 1 Найти общее решение дифференциального уравнения.
Решение: Составим и решим характеристическое уравнение: 2) Теперь нужно найти какое-либо частное решение И вопрос, который вызывает затруднения чаще всего: В каком виде нужно искать частное решение Прежде всего, смотрим на нашу правую часть: После предварительного анализа смотрим на корни характеристического уравнения После правильно выбранного подбора алгоритм пойдёт по накатанной колее. Используем метод неопределенных коэффициентов. Кто не знаком – узнает. Найдём первую и вторую производную:
Подставим (1) Раскрываем скобки. Далее работаем с последним равенством – необходимо приравнять коэффициенты при соответствующих степенях и составить систему линейных уравнений. В картинках процесс выглядит так:
Чтобы было еще проще, новичкам рекомендую предварительно сгруппировать подобные слагаемые: В данном случае система получилась очень простой, и многие из читателей справятся с ней даже устно. Подставляем найденные значения Таким образом, подобранное частное решение неоднородного уравнения: 3) Запишем общее решение неоднородного уравнения: Всё! Ответ: общее решение: Для неоднородных уравнений второго порядка я люблю проводить проверку-«лайт». Сначала я проверяю, правильно ли решил квадратное уравнение. После такой проверки первая часть ответа Осталось проверить, верно ли найдена вторая часть ответа (подобранное частное решение): Подставим Существует и полный вариант проверки, о нём речь пойдет, когда я разберу задачу Коши. Пример 2 Найти общее решение дифференциального уравнения.
Выполнить проверку-«лайт». Это пример для самостоятельного решения, полное решение и ответ в конце урока. Будьте внимательны, пример «с подвохом»! А поэтому повторим, по какой схеме подбирать частное решение: Пример 3 Найти общее решение неоднородного дифференциального уравнения.
Решение: Составим и решим характеристическое уравнение: 2) Выясняем, в каком виде нужно искать частное решение Сначала смотрим на правую часть и выдвигаем первую гипотезу: раз в правой части находится экспонента, умноженная на константу Далее смотрим на корни характеристического уравнения После того, как подобран корректный вид частного решения, алгоритм работает стандартно, единственное, вы должны уметь уверенно находить производные, в частности, использовать правило дифференцирования произведения Найдем первую и вторую производную: Подставим Что сделано? Подстановка, упрощение, сокращение, и в конце – приравнивание к исходной правой части Здесь повезло: из последнего равенства Таким образом, частное решение: 3) Составляем общее решение неоднородного уравнения: Ответ: общее решение: Подчеркиваю, что всегда полезно выполнить «быструю» проверку, проверив, по крайне мере, подобранное частное решение Думаю, что после трёх разобранных примеров вы уже понимаете, как и на каком этапе надо использовать справочный материал Как подобрать частное решение неоднородного уравнения? Теперь всем читателям, в том числе чайникам, рекомендую прочитать справку полностью. Что произойдет, если мы неправильно подберём вид частного решения? Вот в только что разобранном примере мы искали частное решение в виде |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 171. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
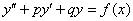 , откинуть правую часть:
, откинуть правую часть: 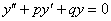 – и найти общее решение. Данная задача подробно разобрана на уроке Однородные уравнения второго и высших порядков. Общее решение однородного уравнения я привык обозначать буквой
– и найти общее решение. Данная задача подробно разобрана на уроке Однородные уравнения второго и высших порядков. Общее решение однородного уравнения я привык обозначать буквой 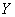 .
.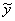 неоднородного уравнения. Сделать это можно так называемым способом подбора частного решения с применением метода неопределенных коэффициентов.
неоднородного уравнения. Сделать это можно так называемым способом подбора частного решения с применением метода неопределенных коэффициентов.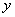 неоднородного уравнения. Это совсем легко:
неоднородного уравнения. Это совсем легко: 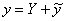 . Совершенно верно – следует просто приплюсовать завоёванные трофеи.
. Совершенно верно – следует просто приплюсовать завоёванные трофеи.

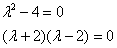
 – получены различные действительные корни, поэтому общее решение:
– получены различные действительные корни, поэтому общее решение: 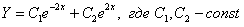
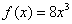 . Тут у нас многочлен третьей степени. По идее, частное решение тоже следует искать в виде многочлена третьей степени:
. Тут у нас многочлен третьей степени. По идее, частное решение тоже следует искать в виде многочлена третьей степени: 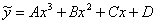 , где
, где 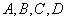 – пока ещё неизвестные коэффициенты (числа). Образно говоря, нужно посмотреть на правую часть неоднородного уравнения и «собезьянничать» её, но уже с неопределёнными коэффициентами. Вариант подбора, который «сразу приходит в голову», я неформально буду называть обычным, обыкновенным или штатным случаем.
– пока ещё неизвестные коэффициенты (числа). Образно говоря, нужно посмотреть на правую часть неоднородного уравнения и «собезьянничать» её, но уже с неопределёнными коэффициентами. Вариант подбора, который «сразу приходит в голову», я неформально буду называть обычным, обыкновенным или штатным случаем.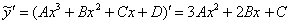

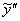 в левую часть неоднородного уравнения:
в левую часть неоднородного уравнения:
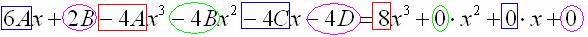
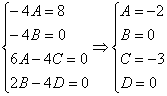
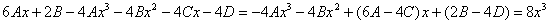 , и только потом составлять систему.
, и только потом составлять систему.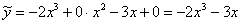
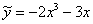
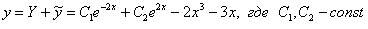
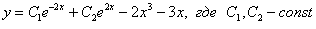
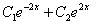 (общее решение однородного уравнения) будет гарантировано правильной.
(общее решение однородного уравнения) будет гарантировано правильной.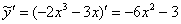
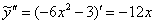
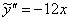 в левую часть неоднородного уравнения:
в левую часть неоднородного уравнения: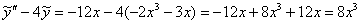 – получена правая часть исходного уравнения, значит, частное решение
– получена правая часть исходного уравнения, значит, частное решение 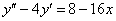
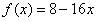 и подбираем первоначальный «штатный» вид частного решения
и подбираем первоначальный «штатный» вид частного решения 
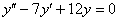
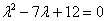
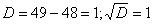
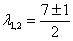
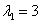 ,
, 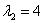 – получены различные действительные корни, среди которых нет нуля, поэтому общее решение:
– получены различные действительные корни, среди которых нет нуля, поэтому общее решение:  .
. , то частное решение, по идее, нужно искать в виде
, то частное решение, по идее, нужно искать в виде 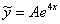
 , где
, где 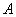 – пока еще неизвестный коэффициент, который предстоит найти.
– пока еще неизвестный коэффициент, который предстоит найти.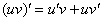 . В ходе вычислений я не буду подробно расписывать производные.
. В ходе вычислений я не буду подробно расписывать производные.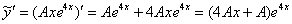
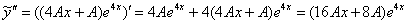
 ,
, 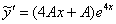 и
и 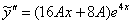 в левую часть неоднородного уравнения:
в левую часть неоднородного уравнения: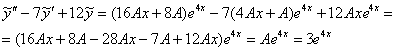
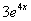 .
.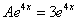 автоматически получаем
автоматически получаем 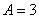 .
.
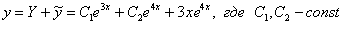

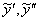 , провести подстановку. Но далее перед глазами возникнет грустный факт: у нас не получится красивого финального равенства
, провести подстановку. Но далее перед глазами возникнет грустный факт: у нас не получится красивого финального равенства 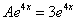 , грубо говоря, «ничего не сойдётся»:
, грубо говоря, «ничего не сойдётся»: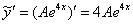
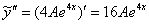
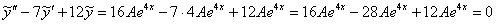
 .
.