
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Коэффициент удельного давленияСтр 1 из 2Следующая ⇒ Тема: Качественные параметры зацепления и выбор коэффициентов смещения при исправлении колёс
1. Коэффициент перекрытия при эвольвентном зацеплении прямозубых колес Коэффициент скольжения Коэффициент удельного давления Выбор коэффициентов смещения для передач с внешними зубьями. Блокирующие контуры 5. Эвольвентное косозубое зацепление
Качественные параметры зацепления дают возможность оценить передачу в отношении плавности и бесшумности зацепления, возможного износа и прочности зубьев и сравнить ряд передач по этим показателям.
1. Коэффициент перекрытия при эвольвентном зацеплении прямозубых колес Коэффициент перекрытия характеризует непрерывность и плавность зацепления. Для того, чтобы передача была плавной и непрерывной, необходимо чтобы работа одной пары зубьев перекрывалась работой следующей пары зубьев. Коэффициент перекрытия определяется
где τ1 и τ2 - - угловой шаг 1-го и 2-го колеса, соответственно.
(а1а2) – длина активной линии зацепления. Выразим длину активной линии зацепления через число зубьев и угол зацепления
Учитывая, что
Как видно из этого выражения  Из треугольника О1N1a1, Рекомендуется брать для тихоходных передач Коэффициент скольжения
Коэффициент скольжения учитывает влияние геометрических и кинематических параметров на величину проскальзывания, а, следовательно, и износа профилей зубьев в процессе зацепления. При зацеплении двух колес профиль одного зуба перекатывается со скольжением по профилю другого зуба. Наличие скольжения при одновременном нажатии одного профиля на другой приводит к износу профилей.
Коэффициенты скольжения для шестерни и зубчатого колеса определяются выражениями
где
определить через радиусы начальных окружностей колёс, а радиусы кривизны профилей зубьев в точке контакта (К) равны расстоянию от этой точки до точки касания основной окружности N1 и N2 (по свойству эвольвенты), выражения для определения коэффициентов скольжения можно записать в следующем виде
Подставив в полученные выражения граничные положения точки контакта (N1 ,W и N2 ), можно увидеть (см. рисунок) что, коэффициент скольжения изменяется от +1 у вершины зуба до -∞ -у ножки зуба, проходя через 0 в полюсе зацепления. Но так, как точка контакта при вращении колёс перемещается на линии зацепления от точки а2, до точки а1, то коэффициент скольжения у ножки зуба имеет конечное значение (см. на рисунке заштрихованную зону), хотя, как правило, большее, чем при вершине зуба. В полюсе зацепления скольжение отсутствует (чистое перекатывание). С учетом того, что зуб колеса участвует в зацеплении меньшее число раз, чемзуб шестерни, целесообразно сопоставлять величины
Коэффициент удельного давления Этот коэффициент учитывает геометрию профилей зубьев на величину контактных напряжений, которые могут достигать значительной величины и приводить к выкрашиванию материала на рабочей поверхности зубьев. Контактные напряжения определяются по формуле Герца
Для текущего момента, исходя из свойств эвольвенты, для внешнего зацепления можно записать
Коэффициентом удельного давления λ называется отношение
Коэффициент λ не зависит от модуля, так как ρ пропорционален модулю, зависит от положения точки контакта на линии зацепления и минимален в начале и в конце зацепления за счёт перекрытия в зацеплении.
|
||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 406. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


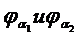 - угол торцевого перекрытия (угол, на который поворачивается колесо от начала входа в зацепление пары зубьев до выхода из зацепления этой же пары зубьев)
- угол торцевого перекрытия (угол, на который поворачивается колесо от начала входа в зацепление пары зубьев до выхода из зацепления этой же пары зубьев) ;
; 
 ;
; 


 во втором слагаемом заменили на
во втором слагаемом заменили на  ,так как
,так как или
или  или
или
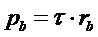 получим аналитическое выражение для коэффициента перекрытия
получим аналитическое выражение для коэффициента перекрытия
 не зависит от модуля, а зависит от числа зубьев и коэффициентов смещения. С увеличением суммарного положительного смещения коэффициент перекрытия уменьшается.
не зависит от модуля, а зависит от числа зубьев и коэффициентов смещения. С увеличением суммарного положительного смещения коэффициент перекрытия уменьшается.  , тогда
, тогда  , а
, а 
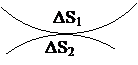 Величина проскальзывания профилей характеризуется коэффициентом скольжения.
Величина проскальзывания профилей характеризуется коэффициентом скольжения.

 радиусы кривизны в точке контакта (К) профилей зубьев первого и второго колеса. С учётом того, что передаточное отношение можно
радиусы кривизны в точке контакта (К) профилей зубьев первого и второго колеса. С учётом того, что передаточное отношение можно


 и
и  через u12. Это имеет особое значение при большихпередаточных отношениях.
через u12. Это имеет особое значение при большихпередаточных отношениях. 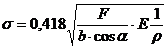
 где F- окружная сила взаимодействия зубьев; b- ширина зубчатых колёс; Е – приведенный модуль упругости материалов колёс (Е = 2Е1Е2/(Е1+Е2)); ρ – приведённый радиус кривизны эвольвентных профилей зубьев в точке контакта(
где F- окружная сила взаимодействия зубьев; b- ширина зубчатых колёс; Е – приведенный модуль упругости материалов колёс (Е = 2Е1Е2/(Е1+Е2)); ρ – приведённый радиус кривизны эвольвентных профилей зубьев в точке контакта(  где + - для внешнего зацепления, а – -для внешнего зацепления).
где + - для внешнего зацепления, а – -для внешнего зацепления).
