
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
УРАВНЕНИЕ ЛИНИИ НА ПЛОСКОСТИСтр 1 из 2Следующая ⇒
1. Фигурой называется любое множество точек. Условием, определяющим фигуру в данной системе координат, называется уравнение, неравенство или их система, которым 1) удовлетворяют координаты точек, принадлежащих фигуре, и 2) не удовлетворяют координаты точек, не принадлежащих этой фигуре. Уравнением фигуры называется уравнение, определяющее эту фигуру в данной системе координат. Определение. В аффинной системе координат Оху на плоскости уравнение Ф(x,y)=0 (1) определяет линию и называется уравнением линии в этой системе координат, если координаты х, у любой точки, принадлежащей линии, удовлетворяют этому уравнению, а координаты точки, не принадлежащей линии, ему не удовлетворяют Определение Линия (на плоскости) называется алгебраической, если в некоторой аффинной системе координат ее уравнение имеет вид Ф(x,y)=0 , где Ф(x,y) – многочлен от переменных х и у, то есть сумму конечного числа слагаемых вида аmkхmуk (m,kÎZ, m³0, k³0, аmn ÎR). При этом степень члена аmkхmуk - число m+k, степень многочлена Ф(х,у) -наивысшая из степеней всех его членов. Определение. Степень многочлена Ф(х,у) называется порядком алгебраической линии (1) Теорема. Понятие алгебраической линии и ее порядка не зависит от выбора аффинной системы координат. □Пусть даны две аффинные системы координат на плоскости: I=(О, Формулы перехода от I к II имеют вид: Чтобы получить уравнение g в системе II, подставим (2) в (1) При этом в правой части уравнения получим сумму слагаемых вида amk(  Если в проведенных рассуждениях поменять ролями системы координат I и II, то получим, что указанное алгебраическое уравнение в системе II имеет степень не ниже чем n, Иначе переход от II к I повысил бы степень уравнения. Таким образом, линия g определяется в новой системе координат II алгебраическим уравнением степени n. ■ Определение. Всякая неалгебраическая линия называется трансцендентной. ПРИМЕРы. 1)Уравнение х3у+х–у=0 определяет алгебраическую линию 4-го порядка, а уравнение х+sin у=0 задает трансцендентную линию. 2) Уравнеиех2+х=0 определяет линию 2-го порядка. Заметим, что х2+х=х(х+1), а значит линия распадается на две линии, определяемые уравнениями х=0 и х+1=0. 3) В некоторой пдск на плоскости уравнение (х-а)2+(у-b)2= r 2 (3) определяет окружность с центром М0(a,b) и радиусом r. В самом деле, окружность w – это есть множество точек, удаленных от точки М0 на расстояние r, то есть точка М(х,у)Îw Û М0М=r Û Если М1(х1, у1)Ï w Û М0М1¹r Û координаты любой точки, не лежащей на w, не удовлетворяют уравнению (3). Уравнение окружности радиуса r >0 с центром в начале координат имеет вид: х2 + у2 = r2. (3¢) Замечание. Уравнение окружности (3) можно записать в виде х2 + у2 +Аx+By+С = 0, (4) где A=-2a, B=-2b, С=a2+b2-R2. Т.е. окружность – линия 2-го порядка. Однако, уравнение вида (4) не всегда является уравнением окружности. Пусть в некоторой пдск задано уравнение х2+у2+Аx+By+С=0. Выясним, какое множество точек на плоскости определяет это уравнение. □ Выделим полные квадраты в левой части: а) если А2+B2-4С>0, то (4) - окружность с центром б) если А2+B2-4С=0, то уравнению (4) удовлетворяет единственная пара чисел х= в) если А2+B2-4С<0, то уравнению (4) вовсе не удовлетворяют никакие пары действительных чисел, то есть оно не определяет ни одной (действительной)точки на плоскости. ■ Следствие. Не всякое уравнение вида (1) определяет на плоскости линию. 2.Для аналитического представления линии часто бывает удобным выражать переменные координаты х и у точек этой линии через третью вспомогательную переменную (параметр): х = j(t), у = ψ(t), (5) где функции j(t) и ψ(t) - непрерывны по параметру t в некоторой области изменения этого параметра. Уравнения (5) называются параметрическими уравнениями линии.
Для любой точки М(х,у) этой окружности обозначим через t ориентированный угол между вектором Тогда координаты точки будут определяться так: х = r cos t , у = r sin t (6) - параметрические уравнения окружности. Чтобы каждой точке М(х,у) окружности соответствовало единственное значение параметра t, ограничим область его изменения полуинтервалом 0£ t <2p.
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 133. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
, 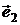 ) и II=(О¢,
) и II=(О¢, ,
,  ). И пусть линия g в системе I определяется уравнением Ф(х,у) = 0, где Ф(х,у) – многочлен степени n.
). И пусть линия g в системе I определяется уравнением Ф(х,у) = 0, где Ф(х,у) – многочлен степени n. ,
,  (2)
(2) )m(
)m(  )k, то есть многочлен от переменных
)k, то есть многочлен от переменных  . Таким образом, понятие алгебраической линии не зависит от выбора системы координат. Кроме того, уравнение линии g в системе II – алгебраическое уравнение степени, не выше, чем n. Следовательно, при переходе к новой системе координат порядок линии увеличиться не может.
. Таким образом, понятие алгебраической линии не зависит от выбора системы координат. Кроме того, уравнение линии g в системе II – алгебраическое уравнение степени, не выше, чем n. Следовательно, при переходе к новой системе координат порядок линии увеличиться не может. 2= r2, где
2= r2, где  2¹ r2, где
2¹ r2, где 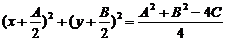 . Сравнивая с (3):
. Сравнивая с (3):  и радиусом
и радиусом  .
.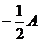 , у=
, у=  В. Значит оно задает единственную точку плоскости с координатами
В. Значит оно задает единственную точку плоскости с координатами  .
. ПРИМЕР. Пусть на плоскости в пдск (О,
ПРИМЕР. Пусть на плоскости в пдск (О,  ,
,  ) найдем параметрическое уравнение окружности радиуса r >0 с центром в т.О.
) найдем параметрическое уравнение окружности радиуса r >0 с центром в т.О.