
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение основных понятийСтр 1 из 6Следующая ⇒ ОСНОВЫ ТЕОРИИ ПЕРЕДАЧИ ИНФОРМАЦИИ Информация (от лат. Informatio - разъяснение, изложение) первоначально - сведения, передаваемые одними людьми другим людям устным, письменным или каким-либо другим способом (например, с помощью условных сигналов, с использованием технических средств связи и т.д.) (БСЭ - III изд., Т. 10, с. 353). С увеличением потока информации (сведений) возникли проблемы описания передачи информации между людьми, между человеком и автоматом, между автоматами. Появились некоторые теории количественной оценки отдельных видов информации (например, в технике связи, кибернетике). Однако полного и всеохватывающего определения информации на сегодня не существует. Классическая теория информации не рассматривает ни вопроса о содержании передаваемых сообщений, ни эффекта воздействия этих сообщений на получателя. Поэтому термин "информация" трактуется как приращение сведений об источнике информации, образующееся у получателя при получении информации. Какая-то доля информации была у нас априорно (или полное ее отсутствие), остальные сведения о состоянии источника нам не известны (имеется априорная неопределенность источника информации). Получение в результате ответа информации об источнике увеличивает у нас количество информации и снимает неопределенность у источника. Рассмотрим изменение объема информации в конкретных случаях. Пусть у нас опыт имеет лишь один исход и не содержит никакой неопределенности, тогда мы заранее знаем исход этого опыта. В результате осуществления опыта мы не получим никакой информации (При передаче сообщения "Волга впадает в Каспийское море" мы не получаем никакого нового сообщения, т.к. нам это было известно заранее).  Пусть опыт имеет два равновероятных исхода (например, прием одной посылки бинарного сигнала). Принимаемый сигнал несет определенную информацию (вероятность каждого сигнала Р = 1/2). Пусть третий опыт связан с возможностью получить один из 10 равновероятных исходов. В этом случае будет большая предварительная неопределенность относительно источника, а принятое сообщение даст более уточненную характеристику состояния источника. Вероятность каждого исхода P(xi) = 1/10 - меньше чем во втором опыте. Вывод: чем меньше априорная вероятность события, тем больше информации несет об источнике сообщение (т.е. тем более неожиданный исход). В третьем случае неопределенность выше. Может показаться, что степень неопределенности определяется числом возможных состояний системы. Однако, в общем случае это не так. Рассмотрим РЭС, техническое состояние которого может быть в двух состояниях: исправно и неисправно. Предположим, что до получения сведений (априори) вероятность исправной системы 0,99, а отказ - 0,01. Такая система обладает малой степенью неопределенности: почти наверное можно предположить, что РЭС исправно. При бросании монеты также два состояния, но степень неопределенности гораздо выше. Вывод: степень неопределенности системы определяется не только числом возможных состояний, но и вероятностями состояний. Поэтому естественно предположить, что количественной мерой неопределенности отдельного сообщения, а также непередаваемой им информации может быть величина, обратная его априорной вероятности 1/P(xi) (что и предложил Р.Хартли в 1928 г.). Однако, такая мера неудобна (при P(xi) = 1 достоверное событие, количество информации оказывается не 0, а 1; кроме того, нет свойства аддитивности, т.к. вероятности двух и более событий перемножаются). Клод Шеннон в 1948 г. ввел логарифмическую меру количества информации.
При этом количество информации, содержащееся в сложном сообщении, представляющем совокупность событий xi и xj будет
Свойства меры Шеннона: 1. Логарифмическая мера обладает свойствами аддитивности. 2. В случае события с одним исходом, детерминированные, т.е. определенные сообщения I(x) = 0. 3. Величина информации растет с ростом неожиданности исхода (т.к. обратно пропорциональна вероятности события). 4. Значение информации ³0 (положительна). Рассматриваемые свойства относятся к дискретной системе. Так как информация случайна, то нужна средняя мера оценки информации (среднее на одно сообщение). I(x) = M[1][-loga(P(xi)] = В основе количества информации лежит априорная неопределенность сообщения, поэтому полученное выражение называют еще "энтропией" (термин заимствован из термодинамики, где аналогичное выражение характеризует среднюю неопределенность состояния системы молекул вещества). Несмотря на совпадение выражений для I(x) и H(x) энтропия и количество информации принципиально различны. Информация рассматривается в связи со своей противоположностью – энтропией. Энтропия определяет среднюю неопределенность источника (возможный объем информации у источника), информация связывается у нас с получением сообщения. Единица измерения информации зависит от выбора основания logа log2 – binary digit = бит (двоичная единица). В основном используется бит. log10 – decimal digit = дит. loge – natural digit = нат. Свойства энтропии: 1. H – вещественна, положительна, >0, ограничена т.к. P()<1. 2. H = 0 для детерминированных сообщений (из определения). 3. H – max, если все события равновероятны. Для доказательства воспользуемся методом неопределенного множителя Лагранжа (l). Составим вспомогательную функцию:
Так как
Необходимо найти max значение Fi по переменной P(x)i, для этого продифференцируем и приравняем = 0:
Для нахождения максимального значения найдем экстремум функции: ¶Fi/¶ Р(хi) = 0 log2 Р(хi) = -log2ℓ - λ = const (i =1, 2, 3, …, n) откуда Р(хi) = const = 1/n Что и требовалось доказать (не зависят от номера i), что только тогда, когда все Р(хi) одинаковы 1/n. Максимальное значение энтропии
4. Энтропия бинарной системы (2-х альтернативной) изменяется Р(х1) + Р(х2) = 1. Н(х) = -Р(х1)log2Р(х1) - Р(х2)log2Р(х2) = -Р(х1)log2Р(х1) - [1-Р(х1)]log2[1-Р(х1)]. Если Р(х1) = 0, Р(х2) = 1 Н(х) = 0 Р(х1) = 1, Р(х2) = 0 Н(х) = 0. Максимум будет, если Р(х1) = Р(х2) = 0,5. Н(х) = -log2(1/2) = 1 дв. ед.
Рис. 2.1 Литература: [1] стр. 8, 128-11. [2] стр. 224-227. [3] стр. 101-105.
Контрольные вопросы: 1. В чем недостатки меры информации по Хартли? 2. Чему равна энтропия системы, если ее состояние неизвестно? 3. При каком распределении вероятностей системы ее энтропия достигает максимума? 4. Может ли быть энтропия отрицательной величиной? 5. Чему равна энтропия бинарной системы при равновероятных состояниях элементов системы?
Энтропия сложных сообщений Рассмотрим энтропию объединенной системы. Под объединением двух систем с возможными состояниями Обозначим через P(yy/xi) условную вероятность того, что система Определим теперь энтропию системы Y при условии, что система Х находится в состоянии xi (частная условная энтропия). Н(Y/xi) = MY[-logP(yj/xi)] = Средняя по множеству всех возможных состояний системы Х условная энтропия (полная условная энтропия) Н(Y/Х) = MХ[Н(Y/xi)] = Условная энтропия H(Y/X) характеризует степень неопределенности системы Y при условии, что состояние системы Х полностью определено. Нетрудно убедиться, что H(Y/X) = H(Y) (2.6) при вероятностной независимости систем Х и Y, а также Н(Y/X) = 0 (2.7) при однозначной (функциональной связи) между системами. Из (2.6) и (2.7) очевидно, что условная энтропия достигает максимума при вероятностной независимости систем. Это утверждение можно строго доказать методами вариационного исчисления, но и так представляется достаточно очевидным, что неопределенность одной системы не может увеличиться от того, что неопределенность какой-то другой системы уменьшилась. Докажем следующую теорему. Если две системы Х и Y объединяются в одну, то энтропия объединенной системы равна энтропии одной из составных частей плюс условная энтропия второй части относительно первой. Н(X,Y) = M[-logP(X,Y)] = M[-log(P(X)×P(Y/X))] = = M[-logP(X)] + M[-logP(Y/X)] = H(X) + H(Y/X). (2.8) В частном случае, когда системы Х и Y независимы H(Y/X) = H(Y) и H(X,Y) = H(X) + H(Y). Так как H(Y/X) ≤ H(Y), то H(X,Y) ≤ H(X) + H(Y), т.е. энтропия сложной системы достигает максимума в случае, когда ее составные части независимы. Теорему об энтропии сложной системы легко распространить на любое число объединяемых систем. Исходя из изложенного, можно объяснить, почему количественное представление информации через энтропию оказалось столь широко применимым. Такое представление обладает следующими достоинствами: 1. Удовлетворяет требованию, предъявляемому к любой мере – аддитивности, по которому общая от нескольких источников информация находится суммированием. 2. Хорошо отражает смысл понятия "информация" - среднее количество информации о системе, которое может быть получено, т.е. энтропия достигает максимума в случае, когда априорные данные о системе отсутствуют (все состояния системы равновероятны) и равно 0, если неопределенность системы отсутствует. Довольно распространенным является случай, когда интересующая нас система событий (случайная величина) изучается не непосредственно, а путем изучения другой системы, связанной с первой вероятностно. Оценим взаимную информацию систем. Пусть нас интересует система Х. Возможные ее состояния определяются априорными вероятностями Р(х1), Р(х2), …, Р(хn). Пусть также имеется система Y, вероятностно связанная с системой Х (известны условные вероятности P(xi/yk). При получении сообщения, что система Y находится в k-м состоянии, изменилось распределение вероятности системы Х, т.е. мы получили определенную информацию о системе Х. Приращение информации об i-том состоянии системы Х
Эта информация называется информацией "от события к событию". В среднем по всем возможным состояниям системы Х приращение информации
Эта величина называется средней частной информацией. Средняя по всем возможным состояниям системы Y информация о системе Х
Симметричность записи выражения (2.9) относительно Х и Y означает, что IY→X = IX→Y = YX↔Y = I(X,Y) = H(X) – H(X/Y) = H(Y) – H(Y/X). (2.10) Среднее количество информации, получаемое при неполной достоверности сообщений равно разности безусловной априорной информации Н(Х) и условной априорной информации H(X/Y), H(X/Y) трактуется как потеря информации (ненадежность связи). Из выражения (2.8) следует: H(X/Y) = H(X,Y) - H(Y) и подстановка в уравнение (2.10) даст YX↔Y = H(X) – H(X,Y) + H(Y) = H(X) + H(Y) – H(X,Y), где Н(Х,Y) – потеря информации. Подытожим свойства взаимной информации. 1. I(X,Y) ≥ 0,; I(X,Y) = 0, когда Х и Y – независимы. 2. I(X,Y) = I(Y,Х). 3. I(X,Y) ≤ Н(Х); I(X,Y) = Н(Х), когда Н(Х/Y) = 0 при однозначной связи. 4. I(X,Х) = Н(Х) – собственная информация о себе.
Литература: [1] стр. 132-134. [2] стр. 227-230. [3] стр. 106-109.
Контрольные вопросы: 1. Чему равна энтропия объединения при независимости входящих в нее систем? 2. Чему равна энтропия объединения при функциональной зависимости входящих в нее систем? 3. Чему равна взаимная информация между независимыми системами? 4. Может ли быть взаимная информация между двумя системами больше, чем наименьшая из энтропий этих систем? 5. Как оценивается потеря информации при передаче ее от одной системы к другой?
|
|||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 187. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
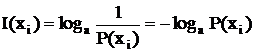 (2.1)
(2.1)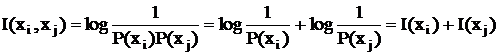 . (2.2)
. (2.2)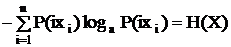 . (2.3)
. (2.3)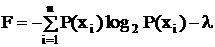 .
.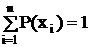 , то на такую величину можно умножить λ:
, то на такую величину можно умножить λ: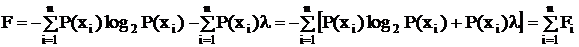 .
.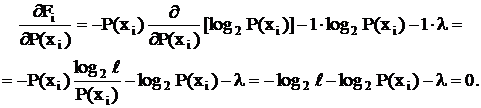
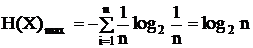 . (2.4)
. (2.4)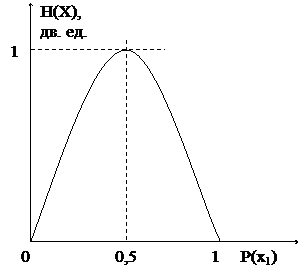
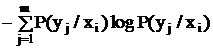 .
.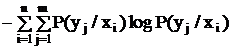 (2.5)
(2.5)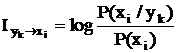 .
.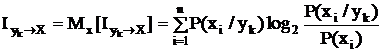 .
.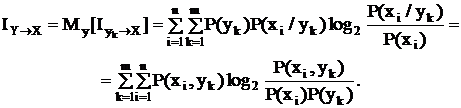 (2.9)
(2.9)