
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Классификация математических моделей, применяемых в землеустройстве. ⇐ ПредыдущаяСтр 2 из 2 При построении математических моделей в землеустройстве возникает вопрос об установлении их класса, степени сложности и конструктивных особенностей. Класс модели определяется целью решаемой задачи и спецификой ее постановки. С точки зрения народнохозяйственного значения землеустроительных проблем и охвата объектов землеустроительного проектирования математические модели можно подразделить на следующие классы.
Рис. 1. Классы экономико-математических моделей в землеустройстве 1. Класс общеотраслевых и межотраслевых математических моделей, обеспечивающих решение задач по прогнозированию и оптимальному планированию использования земельных и связанных с ними ресурсов в республике, крае, области, районе (при составлении схем использования земельных ресурсов). Общеотраслевые и межотраслевые модели применяются при разработке Генеральных схем использования и охраны земельных ресурсов страны (субъекта Федерации), Схем землеустройства административных районов, территорий местной администрации, а также прогнозов и региональных программ по использованию земель, технико-экономического обоснования. 2. Класс моделей межхозяйственного (территориального) землеустройства, позволяющих решать задачи по межхозяйственному устройству территории. К этому классу относятся задами по определению оптимальных размеров землепользований и рациональному размещению производства на территории, по наиболее целесообразной ликвидации недостатков в использовании земель, по установлению наилучшего размера населенных пунктов и их территориальному размещению и др. Модели территориального землеустройства позволяют решать задачи потерриториальному устройству территории, образованию и оптимальному размещению землепользований и землевладений сельскохозяйственного и несельскохозяйственного назначения, установлению границ административно-территориальных образований и т. п. К данному классу моделей относятся задачи по определению размеров хозяйства, рациональному размещению производства на территории, ликвидации чересполосицы и т.д.  3. Класс моделей внутрихозяйственного землеустройства. Модели этого класса предназначены для решения вопросов наиболее полного рационального и эффективного использования земель и организации производства в конкретных сельскохозяйственных предприятиях. Основными задачами данного класса являются следующие: установление оптимального сочетания отраслей, состава и площадей угодий, определение видов, количества и площадей и севооборотов и их размещение, рациональная организация кормопроизводства, планирование грузоперевозок, планирование комплекса мелиоративных работ, оптимальная трансформация угодий, установление оптимальных размеров производстве иных подразделений хозяйств и др. Модели внутрихозяйственного землеустройства применяются для решения вопросов рациональной организации использования земли в конкретных сельскохозяйственных предприятиях. Основными задачами являются следующие: установление оптимального сочетания отраслей сельскохозяйственного производства; состава и площадей угодий, определение видов, типов и количества севооборотов, оптимизация кормопроизводства и т.д.
4 Класс моделей задач рабочего проектирования. Модели задач рабочего проектированияобеспечивают решение конкретных задачи при составлении проектов на отдельные землеустроительные мероприятия: строительство орошаемых культурных пастбищ, внедрение системы земледелия, выполаживание оврагов, строительство скотопрогонов и др. Сложность математических моделей зависит от числа учитываемых факторов и характера взаимосвязи между ними, от наличия, точности и достоверности исходной информации и непосредственно от изучаемого процесса или явления. Сложностью определяются и конструктивные особенности моделей (число неизвестных, их степени, количество условий, виды целевой функции и др.). Для решения землеустроительных задач различных классов используется разнообразное количество математических моделей позволяющих анализировать использование земельных ресурсов, выявлять определенные тенденции и находить оптимальные варианты устройства территории. Все модели подразделяются на три большие группы: I группа - Экономико-математические II группа- Экономико-статистические III группа - Аналитические. Экономико-математические модели используются для разработки оптимальных реакций проекта землеустройства, балансовые для дальнейшего проектирования и обоснования принятых решений (балансы кормов, труда, расчеты населения на перспективу и т.д.) Экономико-статистических моделей используются для анализа производства, подготовки необходимой информации для использования оптимизационных методов, проведении оценки проектировочных решений. Аналитические модели применяются в целях подготовки исходной информации и обоснования проектных решений. С их помощью рассчитывают рабочие уклоны, определяют среднюю условную длину полей и рабочих участков, находят различные технические параметры, используемые для проектирования и т.д.
Математические модели, применяемые в землеустройстве, представлены в виде обобщенной схемы на рис. 2. Классификация экономико-математических моделей предложена Браславцем М.Е. В зависимости от степени определенности информации, используемой в математических моделях, они делятся на два вида: детерминистические и стохастические. Детерминистические модели предполагают жесткие функциональные связи, основаны на информации, которая является или считается абсолютно-точной. В детерминистических моделях результат полностью и однозначно определяется набором независимых переменных. Детерминистические модели делятся на балансовые и оптимизационные. Стохастические модели основаны на информации, носящей вероятностный (стохастический) характер. Эти модели описывают явления и процессы, которые зависят от случайных величин, подчиняющихся законам теории вероятности. Обработка информации осуществляется методами математической статистики. Аналитические модели основаны на применении классических математических методов (алгебры, геометрии, дифференциального и интегрального исчисления), а также строятся на доказательстве различных теорем, выводе формул. Аналитические модели имеют вид формул и функциональный характер. Аналитические модели рассматриваются в курсе землеустроительного проектирования, применяются в целях подготовки исходной информации и обоснования проектных землеустроительных решений, включают в себя взаимосвязи в виде точных алгебраических выражений. Аналитические модели имеют функциональный характер, когда каждому набору значений независимых переменных (факторов) соответствует строго определенное значение результата. Например, с помощью аналитических моделей рассчитывают средние рабочие уклоны, условную длину поля (рабочего участка), находят различные технические параметры, используемые для проектирования. Экономико-статистические модели основаны на использовании теории вероятности и математической статистики (корреляционного, регрессивного и дисперсионного анализа) Главное место среди стохастических моделей занимают производственные функции, представляющие собой уравнения связи результата производства (зависимой переменной) и факторов производства (аргументов). .Например, модель максимизации полезности потребителем или прибыли фирмой; модель прогнозирования урожайности сельскохозяйственных культур. Производственные функции используются для анализа уровня использования земли, производства, подготовки информации для применения оптимизационных методов, оценки и обоснования проектировочных землеустроительных решений.
Функциональныеэкономико-статистические модели аналогичны аналитическим моделям, но основаны на статистической информации. Данные модели встречаются в землеустройстве редко из-за неоднозначности взаимосвязи между результатом и факторами-аргументами. Корреляционныеэкономико-статистические модели основываются на корреляционных уравнениях связи между факторами и результатом. Они описывают неоднозначную зависимость результата от факторов в силу объективных (природа моделируемого объекта) и субъективных (погрешности исходной информации) причин. К объективным причинам относится, например, влияние климатических условий на величину урожайности, к субъективным – влияние выбранных разработчиком модели значений технолого-экономических показателей и т.п. Не всегда можно четко разделить объективные и субъективные причины, влияющие на результативный показатель, но тем не менее корреляционные экономико-статистические модели более адекватно описывают те или иные реальные процессы и явления, чем функциональные. Балансовые моделиприменяются для обоснования проектных решений и определения наилучших пропорций при организации сельскохозяйственного производства. Балансовые модели представляют собой систему различного рода межотраслевых, внутриотраслевых, хозяйственных и др. балансов: баланс технических ресурсов, кормов, труда, удобрений, трансформации и перераспределения земель. Оптимизационные моделиоснованы на методах математического программирования, позволяющих находить экстремальные (минимальные или максимальные) значения целевой функции по перечню основных переменных при заданных ограничениях. Оптимизационные экономико-математические модели применятся для разработки наилучших проектных землеустроительных решений. Например, решается задача по определению размеров крестьянского (фермерского) хозяйства (искомые переменные – общая земельная площадь, площадь пашни, состав земельных угодий и отраслей), которые, исходя из специализации хозяйства, его трудообеспеченности и фондообеспеченности (основные ограничения), давали бы максимальную прибыль (максимальное значение целевой функции). Оптимизационные модели в землеустройстве делятся на две разновидности: комбинированные и дифференцированные. Комбинированное моделирование предполагает решение всех вопросов землеустроительного проекта комплексно по всем составным частям и элементам проекта. Этот вид моделирования является более правильным, однако он приводит к громоздким задачам, решение которых затруднено. Дифференцированное моделирование заключается в последовательном решении частных задач проекта в сочетании с традиционными методами. Модели при этом получаются значительно меньшего объема и их решение существенно облегчается. Применение дифференцированного моделирования в землеустройстве объясняется сложностью и многообразием решаемых вопросов. Этапы построения моделей. Экономико-математическое моделирование в землеустройстве проводится в несколько этапов, основными из которых являются: 1) постановка задачи (словесная формулировка с экономическим анализом количественных зависимостей); 2) математическая формулировка задачи (составление экономико-математической модели); 3) сбор необходимых данных в составление исходной матрицы; 4) решение задачи; 5) анализ полученных результатов. Первый этап -Постановка экономико-математической задачи. Первый этап предполагает установление объекта моделирования, его описание, формулировку цели задачи и выбор критерия оптимальности. · формулируется цель (выбирается критерий оптимальности), · устанавливается объект и предмет исследования, · выделяются структурные или функциональные элементы, соответствующие данной цели, · выявляются наиболее важные качественные характеристики этих элементов, · словесно формулируется задача и · описываются логические взаимосвязи между элементами модели, определяются переменные. Критерий оптимальности– это математические выраженная целевая установка задачи. Виды критериев оптимальности: - максимум прибыли (чистого дохода); - максимум стоимость валовой (товарной) продукции; - минимум производственных затрат; - минимум земельной площади и др. Второй этап. Математическая формулировка задачи. Построение экономико-математической модели · Установление символических, индексных и других обозначений для учета характеристик объекта землеустройства; · Определение перечня переменных; · Построение ограничений (уравнений и неравенств) для установления взаимосвязи между искомыми неизвестными и условиями задач · Математическое выражение целевой функции. Третий этап -Сбор исходной информации. Состав информации: · объемыимеющихся ресурсов (земельных; трудовых; материальных: техника, органические и минеральные удобрения, оросительная вода, семена, посадочный материал; собственные и привлекаемые финансовые средства и др.); · технико-экономические (технолого-экономические) коэффициенты, характеризующие нормы затрат ресурсов на единицу площади или проводимой продукции, объемы производства продукции с единицы площади, продуктивность поголовья и др.; · оценкиэффективности производства, участвующие в построении целевой функции задачи. Четвертый этап -Решение задачи. · Выбор метода решения (графический, симплексный, распределительный). · Решение задачи; · Контроль решения; · Корректировка решения (в случае необходимости). Пятый этап - Анализ полученных результатов. · Установление найденного решения задаче оптимизации. · Выявление несоответствий и ошибок в вычислениях, · Повторное решение (в случае необходимости) Землеустроительные проблемы тесно связаны с экономическими вопросами развития сельскохозяйственных предприятий. Поэтому целевые установки отдельных задач в основном определяют экономический результат, который должен, быть достигнут при решении вопросов использования земель, а, следовательно, и критерий оптимальности поставленной задачи. При решении землеустроительных задач применяются различные критерии оптимальности. Общим правилом их построения является условие оптимального сочетания площади, обеспеченности скота кормам и т.д. Составление экономико-математической модели заключается в установлении связи между исходными данными и исковыми неизвестными в виде уравнений и неравенств. Так, например, при решении вопросов трансформации угодий устанавливается связь между наличием мелиоративного фонда, затратами на перевод угодий в другие виды и общим объемом капиталовложений, отпущенных на трансформацию. При этом определяется эффективность капиталовложений. Кроме того, устанавливается зависимость между размерами трансформации и наличием в хозяйстве трудовых ресурсов, техники. Намечается компенсация утраченной пашни и других сельскохозяйственных угодий. Экономико-статистическое моделирование осуществляется в следующем порядке: 1) определение цели решаемой задачи, экономический анализ на выявление факторов, влияющих на целевой результат; 2) определение математической формы связи независимых переменных (факторов) и результата; 3) сбор необходимых данных и их обработка; 4) вычисление параметров экономико-статистической модели; 5) анализ полученных данных, экономическая оценка и интерпретация модели. Экономико-статистические модели могут быть представлены в виде производственных функций. Полученные при реализации моделей данные анализируют, в случае необходимости корректируют применительно к конкретным природно-экономическим условиям и используют для целей проектирования и обоснования принятых решений. |
|||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 1528. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 Виды математических моделей, применяемых при землеустройстве
Виды математических моделей, применяемых при землеустройстве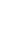 Экономико-статистические модели делятся на функциональные и корреляционные.
Экономико-статистические модели делятся на функциональные и корреляционные.