
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
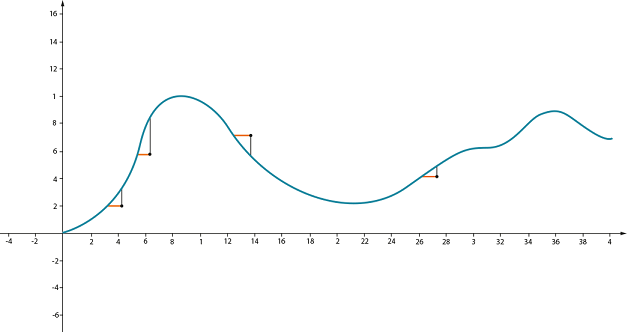
Геометрический смысл производнойСтр 1 из 2Следующая ⇒ Лекция 2-7 Производная Монотонность, выпуклость. Касательная к графику в точке Определение производной и ее смысл Пусть есть тропинка, по которой можно идти то вверх, то вниз, не сворачивая при этом ни вправо, ни влево
Допустим, мы хотим понять, насколько крутой уклон нас ждет впереди. Чтобы измерить эту крутизну, нужно понять, насколько сильно (круто) увеличивается высота при перемещении вперед на единицу расстояния:
Если мы поднимаемся, то K>0, если спускаемся, K<0. Если дорога ровная, без уклона, то K=0.
Возникает вопрос, что взять за единицу расстояния. Если взять слишком большую величину, может оказаться так, что это расстояние включит в себя, например, холм, и мы не поймем, что в процессе уклон будет меняться.
Чтобы не сталкиваться с такой проблемой, в математике берется бесконечно малая величина, то есть в нашем примере крутизна уклона будет измеряться как
Собственно, это и будет производная. Она показывает скорость изменения функции в данной точке.
Производная функции – это предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует.
Функцию, имеющую конечную производную в данной точке, называют дифференцируемойв этой точке, а процесс вычисления производной - дифференцированием. Функция дифференцируема на множестве точек (например, на отрезке, интервале или на всей области определения), только если она дифференцируема в каждой точке этого множества.
Пример 1 По определению выведите производную для функции
 Правой (левой) производной функции f(x) в точке x0 называется предел справа (слева) отношения приращения функции к приращению аргумента при стремлении последнего к нулю.
Теорема (1) Функция имеет производную в точке При этом Обратное также верно: если в точке
Функцияf(x) называется непрерывнойв точке х0, еслиf(x) имеет пределв точке х0, и этот пределсовпадает со значением функцииf(x0): Функция непрерывна на множестве, если она непрерывна в каждой точке этого множества. График непрерывной функции является непрерывной линией.
Теорема (2) Если функция
Пример 2 Проверить существование производной функции
Производные элементарных функций · · · · · · · · · · · · · ·
Правила вычисления производной · Производнаяконстанты (числа) равнанулю: · · Производнаясуммы (разности) равнасумме (разности) производных: · Производнаяпроизведения: · Производнаяотношения: · Производнаясложнойфункции: еслифункция
Пример 3 Найти производную от
Пример 4 Дана функция
Геометрический смысл производной
Уравнение касательнойк кривой
Фактически это уравнение прямой, проходящей через точку
Пример 5 В каких точках касательная к графику функции
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 150. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.
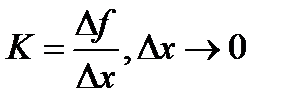 .
.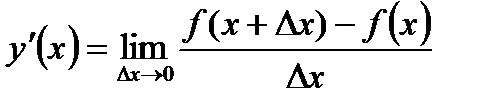
 .
. , если в этой точке существуют и равны между собой производные справа и слева.
, если в этой точке существуют и равны между собой производные справа и слева. .
. .
. имеет производную в точке
имеет производную в точке  в точке х=0.
в точке х=0.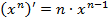

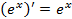

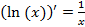



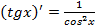






 , гдеc–константа
, гдеc–константа

 при
при 
 имеетпроизводнуювточке
имеетпроизводнуювточке  , афункция
, афункция 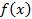 имеетпроизводнуювточке
имеетпроизводнуювточке  , тосложнаяфункция
, тосложнаяфункция 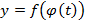 имеетпроизводнуювточке
имеетпроизводнуювточке 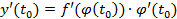
 .
. . Нужно найти
. Нужно найти  и
и  .
. в точке
в точке  равна угловому коэффициенту (тангенсу угла наклона) касательной к графику функции
равна угловому коэффициенту (тангенсу угла наклона) касательной к графику функции  в точке
в точке  .
.
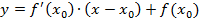
 .
.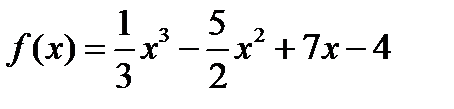 образует с Ох угол в 45 градусов?
образует с Ох угол в 45 градусов?