
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Проверка гипотезы о средних ⇐ ПредыдущаяСтр 2 из 2 Пусть имеются две выборки, характеризующиеся средними значениями Выдвигается гипотеза, что эти средние равны , т. е
Для проверки основной гипотезы используют критерий
Так как Используя свойства дисперсии и предполагая выборки независимыми, получим:
Сделав дополнительное предположение, что дисперсии обеих совокупностей равны, т.е.
Предположение о равенстве дисперсий нуждается в специальной проверке, о чем речь пойдет в следующем разделе. Подставляя это выражение в формулу для критерия, получаем:
Если обе выборки достаточного большого объема (больше 30 элементов), то случайная величина Если нам неизвестна дисперсия генеральной совокупности
Придем к нормально распределенному критерию:
Дальнейшая проверка ведется обычным образом с использованием таблиц функций распределения Лапласа. Если выборки малого объема (элементов менее 30) и применение нормального распределения может привести к ошибкам, для того же критерия Z используют t-распределение Стьюдента с числом степеней свобода k=n1 +n2 -2. Сравнение дисперсий Пусть имеются две нормально распределенные выборки, дисперсии которых равны Так как дисперсии генеральных совокупностей неизвестны, проверка гипотезы осуществляется на основе сопоставления выборочных дисперсий 
или
Распределение этого отношения, называющееся F–распределением Фишера – Снедекора, зависит от двух параметров – чисел степеней свободы числителя и знаменателя:
Критическая область строится в зависимости от вида альтернативной гипотезы: 1. Нулевая гипотеза По заданному α и известным 2. Альтернативная гипотеза В этом случае строим симметричную двустороннюю критическую область с критическими точками
Правая критическая точка находится непосредственно по таблице критических точек распределения Фишера – Снедекора для уровня значимости
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 218. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  , дисперсиями
, дисперсиями  и
и  .
.

 ,
,  , при справедливости нулевой гипотезы
, при справедливости нулевой гипотезы 
 будем иметь
будем иметь  .
.
 получим:
получим: .
.
 и случайная величина
и случайная величина  имеют нормальное распределение, поэтому нормально будет распределен и критерий
имеют нормальное распределение, поэтому нормально будет распределен и критерий  .
. , то её заменяют на несмещенную выборочную оценку
, то её заменяют на несмещенную выборочную оценку 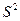 .
.

 ; нулевая гипотеза
; нулевая гипотеза  .
. и
и  . Если отношение
. Если отношение  , если (
, если (  )
) ; если (
; если (  )
) и
и  , где
, где 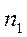 и
и  – объемы выборок. Числа
– объемы выборок. Числа  и
и  указываются в фигурных скобках рядом с вычисленным значением F:
указываются в фигурных скобках рядом с вычисленным значением F:
 . Альтернативная гипотеза
. Альтернативная гипотеза  , если (
, если (  ).
). . Проверка гипотезы H0 сводится к следующему правилу: если отношение выборочных дисперсий
. Проверка гипотезы H0 сводится к следующему правилу: если отношение выборочных дисперсий  , гипотеза H0 отклоняется; если
, гипотеза H0 отклоняется; если 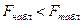 , гипотеза H0 не отклоняется.
, гипотеза H0 не отклоняется. .
. и
и  , определяемыми из неравенств
, определяемыми из неравенств ;
; 
 и степеней свободы
и степеней свободы  .Так как из определения уровня значимости
.Так как из определения уровня значимости  , то выбирая
, то выбирая  , нулевая гипотеза H0 отклоняется, если
, нулевая гипотеза H0 отклоняется, если  гипотеза H0 не отклоняется.
гипотеза H0 не отклоняется.