
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Проверка статистических гипотезСтр 1 из 2Следующая ⇒ Под статистической гипотезой понимают всякое высказывание, которое можно проверить по выборке. Как правило, статистические гипотезы делят на гипотезы о законах распределения и гипотезы о параметрах закона распределения. Наиболее часто встречаются гипотезы, связанные со сравнением выборок. Статистической гипотезой называется всякое непротиворечивое множество утверждений Критерием называется случайная величина Ошибка первого рода состоит в том, что будет отклонена гипотеза  Ошибка второго рода состоит в том, что принимается неверная гипотеза. Вероятность ошибки второго рода обозначается через β . Величина (1– β) называется мощностью данного критерия. α = P{(x1, x2, …, xn) Î S1/H0 }, β = P{(x1, x2, …, xn) Î S0/H1 }. Одновременно снизить ошибку первого и второго рода нельзя, поэтому задача решается разумным компромиссом на основе опыта. В математической статистике принята следующая схема: вероятность ошибки первого рода обычно заранее фиксируют и стараются найти критерий, который при фиксированном α обладает большей мощностью (т.е. ошибка 1-го рода фиксирована, а величина ошибки 2-го рода– наименьшая). Обычно уровень значимости α = 0.05; 0.01 или 0.005 (или меньше), причем его величина зависит от важности задачи: в медицине 0.005, в экономике и технике 0,05. Проверка гипотезы о равенстве вероятностей. Пусть произведено две серии опытов, состоящих соответственно из Спрашивается, значимо или не значимо это расхождение? Указывает ли оно на то, что в первой серии опытов событие A действительно вероятнее, чем во второй, или расхождение между частотами надо считать случайным? Выдвинем двухальтернативную гипотезу В данном случае нуль-гипотеза При достаточно больших
В качестве критерия будем использовать случайную величину Определим критическую точку
Если значение, вычисленное по формуле |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 187. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 относительно свойств распределения случайной величины. Любое из утверждений
относительно свойств распределения случайной величины. Любое из утверждений  называется альтернативой гипотезы. Простейшей гипотезой является двухальтернативная:
называется альтернативой гипотезы. Простейшей гипотезой является двухальтернативная:  В этом случае альтернативу
В этом случае альтернативу  называют нулевой гипотезой, а
называют нулевой гипотезой, а  - конкурирующей гипотезой. Нулевая гипотеза, как правило, утверждает, что отличия статистически незначимы и вызваны статистической изменчивостью.
- конкурирующей гипотезой. Нулевая гипотеза, как правило, утверждает, что отличия статистически незначимы и вызваны статистической изменчивостью. ,где
,где  – значения выборки, которая позволяет принять или отклонить нулевую гипотезу H0. Значения критерия, при которых гипотеза
– значения выборки, которая позволяет принять или отклонить нулевую гипотезу H0. Значения критерия, при которых гипотеза  и
и  опытов. В каждом из них регистрировалось появление одного и того же события А . В первой серии событие А появилось в
опытов. В каждом из них регистрировалось появление одного и того же события А . В первой серии событие А появилось в  опытах, во второй — в
опытах, во второй — в  опытах, причем частота события А в первой серии получилась больше, чем во второй:
опытах, причем частота события А в первой серии получилась больше, чем во второй:  . Разность между двумя частота получилась равной
. Разность между двумя частота получилась равной  .
. , где:
, где:  объясняется случайными причинами,
объясняется случайными причинами,  появления события А в них одна и та же, приближенно равная частоте, которая получится, если обе серии смешать в одну :
появления события А в них одна и та же, приближенно равная частоте, которая получится, если обе серии смешать в одну :  .
. и
и  . Что касается дисперсий
. Что касается дисперсий  и
и  в первой и во второй сериях, то они различны и равны соответственно.
в первой и во второй сериях, то они различны и равны соответственно. ,
, 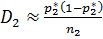
 , которая также имеет приближенно нормальное распределение с математическим ожиданием
, которая также имеет приближенно нормальное распределение с математическим ожиданием  и дисперсией
и дисперсией  , откуда
, откуда 
 для заданного уровня значимости α из уравнения:
для заданного уровня значимости α из уравнения: т.е.
т.е. 
 , больше, чем критическое значение, т.е.
, больше, чем критическое значение, т.е.  , то гипотеза
, то гипотеза