Виды выпуклых многогранников (призма, пирамида). Определение формы и положения многогранника в пространстве. Построение ортогональных проекций многогранных поверхностей.

Модуль 1. «Методы архитектурной графики»

Лекция № 2. Изображения в ортогональном черчении.

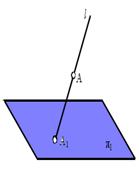
Основные принципы параллельного (ортогонального проецирования).

Проекцией точки А на плоскость проекций ₁ называется точка А₁ pпересечения проецирующей прямой ℓ с плоскостью проекций ₁, проходящей через точку А, (рис. 1.1):

Проекция любой геометрической pфигуры есть множество проекций всех ее точек. Направление проецирующих прямых ℓ и положение плоскостей ₁ определяют аппарат проецирования.

Центральным проецированием называется такое проецирование, при котором все проецирующие лучи исходят из одной точки S – центра проецирования (рис. 1.2).

Рис. 1.1. Проекция точки А на плоскость проекций π1	Рис. 1.2. Пример центрального проецирования	Рис. 1.3. Пример параллельного проецирования

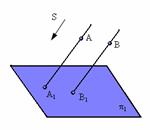
Параллельным проецированием называют такое проецирование, при котором все проецирующие прямые параллельны заданному направлению S (рис. 1.3).

Параллельное проецирование pпредставляет собой частный случай центрального проецирования, когда точка S находится на бесконечно большом расстоянии от плоскости проекций ₁.

При заданном аппарате проецирования каждой точке пространства соответствует одна и только одна точка на плоскости проекций.

Одна проекция точки не определяет положения этой точки в пространстве. Действительно, проекции А₁ может соответствовать бесчисленное множество точек А^’, А^’’, расположенных на проецирующей прямой ℓ (рис. 1.4).

Рис. 1.4. Пример расположения множества точек на проецирующей прямой	Рис. 1.5. Определение положения точки А в пространстве

Для определения положения точки в пространстве при любом аппарате проецирования необходимо иметь две ее проекции, полученных при двух различных направлениях проецирования (или при двух различных центрах проецирования).

Так, из рис. 1.5 видно, что две проекции точки А (А₁ и А₂), полученные при двух направлениях проецирования S₁ и S₂ , определяют единственным образом положение самой точки А в пространстве – как пересечение проецирующих прямых ℓ₁ и ℓ₂, проведенных из проекций А₁ и А₂ параллельно направлениям проецирования S₁ и S₂.

Определение многогранников. Грань, ребро, вершина. Выпуклые и вогнутые многогранники. 

Многогранником называется совокупность таких плоских многоугольников, у которых каждая сторона одного является одновременно стороной другого, но только одного. Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью.Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называются ребрами многогранника, а вершины – вершинами многогранника.

Многогранники могут быть выпуклые и невыпуклые. Многогранник называется выпуклым, если отрезок соединяющий любые две точки, принадлежащие данному многограннику, полностью принадлежит данному многограннику. Многогранник называется невыпуклым, если можно построить отрезок не принадлежащий полностью данному многограннику, но соединяющий две точки, принадлежащие данному многограннику. Выпуклый многогранник, всегда, лежит по одну сторону от плоскости каждой своей грани. Невыпуклый, может быть по разные стороны.

Виды выпуклых многогранников (призма, пирамида). Определение формы и положения многогранника в пространстве. Построение ортогональных проекций многогранных поверхностей.

Предметом нашего изучения будут только выпуклые многоугольники, т.е. такие, которые расположены по одну сторону каждой его грани.
Форма и положение многогранника в пространстве могут быть определены заданием его ребер, основанием и вершиной, если это пирамида, основанием и одним из боковых ребер, если это призма. По существу, построение чертежей призм и пирамид сводится к построению проекций точек (вершин) и отрезков прямых (ребер). Примером многогранников могут служить призмы и пирамиды. На рис. 2 даны ортогональные проекции многогранных поверхностей.

Рис. 2.