
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задание 1. Синтез и исследование логических схем.Стр 1 из 5Следующая ⇒ Министерство образования и науки Российской Федерации Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Национальный исследовательский ядерный университет «МИФИ» Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ
Задания для самостоятельной работы По дисциплине «Основы микропроцессорной техники»
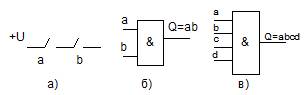
г. Волгодонск, 2012 г. 1. Синтез и исследование логических схем. Цель работы: 1. Исследование логических схем. 2. Реализация логических функций при помощи логических элементов. 3. Синтез логических схем, выполняющих заданные логические функции. Краткие сведения из теории 1.1 Аксиомы алгебры логики. Переменные, рассматриваемые в алгебре логики, могут принимать только два значения - 0 или 1. В алгебре логики определены: отношение эквивалентности (обозначается знаком =) и операции: сложения (дизъюнкции), обозначаемая знаком v, умножения (конъюнкции), обозначаемая знаком & или точкой, и отрицания (или инверсии), обозначаемая надчеркиванием или апострофом'. Функция НЕ (другие названия: отрицание, инверсия) - это функция одного аргумента. Она равна 1, когда ее аргумент равен 0, и наоборот. Обычное обозначение Электронный логический элемент (ЛЭ), реализующий функцию НЕ в виде определенных уровней напряжения, называют инвертором. Инвертор на схемах изображается, как показано на рис. 1,а. Вход - слева, выход - справа, кружок - символ инверсии. Условное изображение инвертора (или любого другого ЛЭ) на схеме может быть повернуто на 90° (вход - сверху, выход - снизу, рис. 1,б). Другие углы поворота и направления входов и выходов не допускаются.  В релейно-контактной технике функцию НЕ реализует нормально замкнутый контакт (рис. 1,в), т.е. такой контакт реле, который замкнут, пока в обмотке нет токового сигнала
Рис.1 Инвертор: а) предпочтительное изображение; б) допустимое изображение; в) реализация НЕ в релейно-контактной технике. Функция И (другие названия: конъюнкция, логическое умножение, AND) - это функция двух или большего числа аргументов. Обозначение: Q= a&b; Q=aÙb; Q=a×b; Q=ab. Читается «Q есть a и b». Функция И равна 1 тогда и только тогда, когда все ее аргументы равны 1. В релейно-контактной технике функция И реализуется последовательным включением нормально разомкнутых контактов (рис. 2,а). Ток в цепи пойдет, когда контакты замкнуты, т.е. находятся в единичном состоянии. Значения функции И для всех комбинаций аргументов a и b приведены в таблице 1 Там же приведены значения и других часто используемых функций, о которых речь будет вестись ниже. Элемент, реализующий функцию И, называют элемент И или конъюнктор. Элемент И часто используют для управления потоком информации. При этом на один его вход поступают логические сигналы, несущие некоторую информацию, а на другой- управляющий сигнал: пропускать - 1, не пропускать - 0. Элемент И, используемый таким образом, называют вентиль (gate). Таблица 1
Функцию И можно построить от любого числа аргументов. На рис. 2,б и в показаны условные изображения двух - и четырехвходового конъюнкторов.
Рис. 2. Конъюнктор: а) реализация операции И на контактах реле; б) условное изображение двухвходового конъюнктора 2И (AND2); в) то же для четырехвходового - 4И (AND4). Функция ИЛИ (другие названия: дизъюнкция, логическое сложение, OR)- это функция двух или большего числа аргументов. Функция ИЛИ равна 1, если хотя бы один из ее аргументов равен 1. Обозначение: Q=aÚ b, Q=a+b. Читается: «Q есть a или b». Условное изображение трехвходового дизъюнктора (3ИЛИ, OR3) показано на рис. 3,а. В релейно-контактных схемах функция ИЛИ реализуется параллельным включением контактов (рис. 3,б).
Рис. 3 Дизъюнктор: а) условное изображение; б) реализация ИЛИ на контактах. Алгебра логики определяется следующей системой аксиом:
1.2 Логические выражения. Запись логических выражений обычно осуществляют в конъюнктивной или дизъюнктивной нормальных формах. В дизъюнктивной форме логические выражения записываются как логическая сумма логических произведений, в конъюнктивной форме - как логическое произведение логических сумм. Порядок действий такой же, как и в обычных алгебраических выражениях. Логические выражения связывают значение логической функции со значениями логических переменных. 1.3 Логические тождества. При преобразованиях логических выражений используются логические тождества:
1.4 Логические функции. Любое логическое выражение, составленное из п переменных xn, xn-1... x1 с помощью конечного числа операций алгебры логики, можно рассматривать как некоторую функцию п переменных. Такую функцию называют логической. В соответствии с аксиомами алгебры логики функция может принимать в зависимости от значения переменных значение 0 или 1. Функция п логических переменных может быть определена для 2п значений переменных, соответствующих всем возможным значениям n-разрядных двоичных чисел. Основной интерес представляют следующие функции двух переменных х и у: f1(х, у) = х · у – логическое умножение (конъюнкция); f2(x, у) = х v у – логическое сложение (дизъюнкция); f3(x, у) = f4(x, у) = 1.5 Логические схемы. Физическое устройство, реализующее одну из операций алгебры логики или простейшую логическую функцию, называется логическим элементом. Схема, составленная из конечного числа логических элементов по определенным правилам, называется логической схемой. Основным логическим функциям соответствуют выполняющие их схемные элементы. 1.6 Таблица истинности. Так как область определения любой функции п переменных конечна (2n значений), такая функция может быть задана таблицей значений f(υi), которые она принимает в точках υi, где i = 0,1...2n—1. Такие таблицы называют таблицами истинности. В таблице 2 представлены таблицы истинности, задающие указанные выше функции. Таблица 2
i = 2x+y - число, образованное значениями переменных. 1.7 Карты Карно и диаграммы Вейча. Если число логических переменных не превышает 5-6, преобразования логических уравнений удобно производить с помощью карт Карно или диаграмм Вейча. Цель преобразований - получение компактного логического выражения (минимизация). Минимизацию производят объединением наборов (термов) на карте Карно. Объединяемые наборы должны иметь одинаковые значения функции (все 0 или все 1). Для наглядности рассмотрим пример: пусть требуется найти логическое выражение для мажоритарной функции fm трех переменных X, Y, Z, описываемой следующей таблицей истинности: Таблица 3. Мажоритарная функция
Составим карту Карно. Она представляет собой нечто похожее на таблицу, в которой наименования столбцов и строк представляют собой значения переменных, причем переменные располагаются в таком порядке, чтобы при переходе к соседнему столбцу или строке изменялось значение только одной переменной. Например, в строке XY таблицы 12.3 значения переменных XY могут быть представлены следующими последовательностями: 00, 01, 11, 10 и 00, 10, 11, 01. Таблицу заполняют значениями функции, соответствующими комбинациям значений переменных. Полученная таким образом таблица выглядит, как показано ниже (таблица 4). Таблица 4. Карта Карно мажоритарной функции
На карте Карно отмечаем группы, состоящие из 2n ячеек (2, 4, 8,...) и содержащие 1, т. к. они описываются простыми логическими выражениями. Три прямоугольника в таблице определяют логические выражения XY, XZ, YZ. Каждый прямоугольник, объединяющий две ячейки, соответствует логическим преобразованиям:
Компактное выражение, описывающее функцию, представляет собой дизъюнкцию полученных при помощи карт Карно логических выражений. В результате получаем выражение в дизъюнктивной форме:
Для реализации функции мажоритарной логики трех логических переменных необходимо реализовать схему, которая при подаче на ее входы трех сигналов формировала бы на выходе сигнал, равный сигналу на большинстве входов (2 из 3 или 3 из 3). Эта схема полезна для восстановления истинного значения сигналов, поступающих на 3 входа, если возможен отказ на одном из входов. Соответствующая схемная реализация приведена на рис. 4.
Рис. 4 Для реализации функции на элементах 2И-НЕ преобразуем полученное выражение в базис элементов И-НЕ, т.е. запишем выражение при помощи операций логического умножения и инверсии. Проверить справедливость каждого из приведенных выражений для fm можно прямой подстановкой значений X, Y, Z из таблицы 3:
Задание 1. Синтез и исследование логических схем. Разработать логические схемы для реализации частично определенных логических функций F 4-х аргументов, заданных таблицами (см. таблицу 1). Каждая комбинация значений аргументов двоичных переменных ABCD отображается числом N, равным: Задача 1.1Разработку провести на базе элементов 2И, 2ИЛИ, НЕ. Задача 1.2Разработку провести на базе элементов2И-НЕ. Задача 1.3 Разработку провести на базе элементов2ИЛИ-НЕ. Таблица 1
Таблица 2
Варианты к задачам 1.1, 1.2, 1.3: №1
№2
№3
№4
№5
№6
№7
№8
№9
№10 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 620. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 . Читается «Q есть не а».
. Читается «Q есть не а». , и размыкается при подаче тока
, и размыкается при подаче тока 


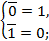



 .
. логическое умножение с инверсией;
логическое умножение с инверсией; – логическое сложение с инверсией.
– логическое сложение с инверсией.






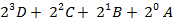 (см. таблицу 2). Минимизацию логической функции проводить с помощью карт Карно.
(см. таблицу 2). Минимизацию логической функции проводить с помощью карт Карно.