
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Пример расчета средней арифметической способом моментов ⇐ ПредыдущаяСтр 2 из 2
Средняя гармоническая простая вычисляется в случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, т.е. когда суммированию подлежат не сами варианты, а обратные им величины:
Средняя гармоническая простая рассчитывается по следующей формуле:
В тех случаях, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение, применяется формула средней гармонической взвешенной:
Пример. По данным табл. 4.4 определить среднюю трудоемкость. Т а б л и ц а 4.4 Пример расчета средней гармонической взвешенной
Средняя квадратическая применяется только тогда, когда варианты представляют собой отклонения фактических величин от их средней арифметической или от заданной нормы. Средняя квадратическая может быть простой и взвешенной и определяется соответственно по формулам:
Пример. По данным табл. 4.5 рассчитать среднюю величину отклонений от заданной нормы. Т а б л и ц а 4.5
 По исходным данным построим табл. 4.6. Т а б л и ц а 4.6 Пример расчета средней квадратической взвешенной
Средняя геометрическая – это величина, используемая как средняя из отношений или в рядах распределения, представленных в виде геометрической прогрессии. Этой средней удобно пользоваться, когда уделяется внимание не абсолютным разностям, а отношениям двух чисел. Поэтому средняя геометрическая используется в расчетах среднегодовых темпов роста.
где
Пример. По данным табл. 4.7 определить среднегодовое увеличение выпуска товарной продукции за пять лет. Т а б л и ц а 4.7 Пример расчета средней геометрической
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 259. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
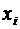 ), руб.
), руб.
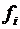 )
)
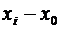
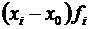
 16500
16500
 16840
16840
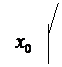
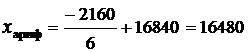 руб.
руб.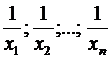
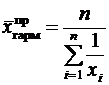
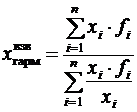 .
.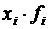 ),
Чел.-ч.
),
Чел.-ч.
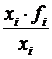
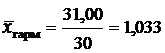 чел. - ч.
чел. - ч.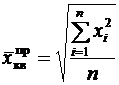 ,
, 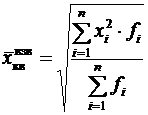 .
.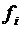 ), шт.
), шт.
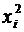
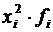
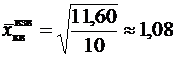 мм.
мм.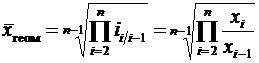 или
или 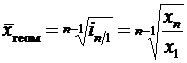 ,
,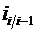 – относительная величина динамики цепная;
– относительная величина динамики цепная; 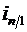 – относительная величина динамики базисная.
– относительная величина динамики базисная.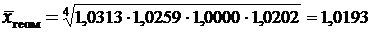 .
.