
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Заработная плата рабочих цехаСтр 1 из 2Следующая ⇒ Тема 4. Средние величины
Содержание задания и требования к нему
По теме 4 студент должен: 1) Продолжить расчёт свой задачи темы 1 (заполненная таблица 1.7) Рассчитать все виды степенных средних (5 простых и 5 взвешенных) по результатам своей темы 1. Сделать выводы: а) по выполнению правила мажорантности; б) о размерах (границах) «вилки» средней простой и о размерах (границах) «вилки» средней взвешенной. 2) Решить задачу, номер которой соответствует варианту. Рассчитать все виды степенных средних (5 простых и 5 взвешенных).
Задача 1. Определить среднюю длительность операции.
Задача 2. Определить среднюю зарплату.
Задача 3. Определить среднюю скорость поезда.
Задача 4. Определить средний процент брака.
Задача 5. Определить среднюю выработку рабочих.
Задача 6. Определить среднюю дальность поездки.
Задача 7. Определить средний процент выполнения плана по отрасли. 
Задача 8. Определить средний процент выполнения плана.
Задача 9. Определить среднюю выработку деталей рабочим.
Задача 10. Определить среднюю заработную плату.
Методические указания к выполнению задания по теме 4
Средняя величина – это обобщающая количественная характеристика уровня варьирующего признака по однородной совокупности. Средние рассчитываются на основе массовых данных правильно статистически организованного массового наблюдения. В зависимости от характера изучаемых явлений, от конкретных задач и целей статистического исследования применяются четыревида средних: – арифметическая; – гармоническая; – геометрическая; – квадратическая.
При расчете различных степенных средних по одним и тем же данным значения средних будут неодинаковыми. Чем выше показатель степени (
Наиболее широкое применение и, следовательно, распространение имеет средняя арифметическая. Средняя арифметическая может быть простой и взвешенной. Средняя арифметическая простая равна сумме произведений значений признака, деленной на их количество.
где
Пример.По данным табл. 4.1 определить среднюю заработную плату рабочего бригады. Т а б л и ц а 4.1 Заработная плата рабочих цеха
Для этого просуммируем зарплату всех рабочих (значение признака) и разделим на количество рабочих (число значений признака):
Если одно и то же значение признака встречается несколько раз, то рассчитывается средняя арифметическая взвешенная по формуле:
где Пример. По исходным данным, приведенным в табл. 4.1, построим вариационный ряд (см. табл. 4.2). Т а б л и ц а 4.2 Пример расчета средней арифметической взвешенной
Средняя арифметическая обладает рядом свойств [2], позволяющих во многих случаях упростить ее расчет. Одним из таких упрощенных методов расчета является способ моментов:
где
Пример. По исходным данным, приведенным в табл. 4.1, построим таблицу для вычисления средней арифметической методом моментов (табл. 4.3). Т а б л и ц а 4.3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 244. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||










 ), тем больше величина средней, т.е. действует правило мажорантности средних:
), тем больше величина средней, т.е. действует правило мажорантности средних:
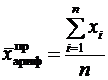 ,
,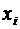 – значение признака у i-ой единицы совокупности;
– значение признака у i-ой единицы совокупности;  – число единиц наблюдения в исследуемой совокупности.
– число единиц наблюдения в исследуемой совокупности. руб.
руб. ,
,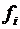 – частота, т. е. число случаев возникновения i-го значения признака.
– частота, т. е. число случаев возникновения i-го значения признака.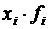
 руб.
руб. ,
, – значение признака имеющего максимальную частоту (условная средняя);
– значение признака имеющего максимальную частоту (условная средняя);  – величины отклонения среднеарифметической от условной средней, которая определяется по формуле:
– величины отклонения среднеарифметической от условной средней, которая определяется по формуле:
 .
.