
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Термодинамические потенциалыСтр 1 из 2Следующая ⇒ Тема 2. МЕТОДЫ ТЕРМОДИНАМИКИ
Если ТС совершает только работу изменения объема (dL0 = 0), основное уравнение термодинамики (1.28) перепишем в виде
Дифференциальная форма уравнения (2.1) позволяет сделать следующий вывод: в состоянии термодинамического равновесия ТС ее внутренняя энергия U представляет собой функцию обобщенных ТД координат (S, V, Nj). ТД переменные (T, -p, mj) выполняют при этом роль обобщенных ТД сил, причем каждая из них выражается через частную производную от внутренней энергии по соответствующей этой силе координате
Соотношения (2.2) определяют внутреннюю энергию равновесной ТС как ТД потенциал или характеристическую функцию
При помощи тождественных преобразований
могут быть получены еще три характеристические функции:
энтальпия
энергия Гельмгольца (свободная энергия)
энергия Гиббса (изобарный потенциал, или просто ТД потенциал)
Основное уравнение термодинамики для этих характеристических функций приобретает три формы записи:
Из (2.3) получаются следующие выражения для обобщенных термодинамических сил:
Энергия Гиббса (ТД потенциал) выделяется из четырех характеристических функций тем, что зависит от интенсивных ТД переменных (р, Т). Так как химический потенциал так же определен как интенсивная переменная, то последнее уравнение (2.3) можно преобразовать к уравнению (2.5): 
с интенсивными переменными в правой части. Для однокомпонентной ТС уравнение (2.5) упрощается:
Согласно определению, энергия Гиббса, подобно внутренней энергии, является экстенсивной величиной и должна обладать свойством аддитивности. Следовательно, функция Ф(p, T, N) однородна по экстенсивной переменной N. Это означает, что увеличение N в a раз приводит к увеличению Ф во столько же раз:
Ф(p, T, aN) = a Ф(p, T, N) .
Дифференцируя последнее равенство по a и полагая a = 1, получим
Таким образом, химический потенциал m представляет собой энергию Гиббса, отнесенную к одной молекуле (или одному молю вещества). Из соотношений (2.6) и (2.7) следует дифференциальное уравнение для химического потенциала:
где s = S/N и v = V/N ‑ удельные величины энтропии и объема. В случае многокомпонентной системы, пользуясь свойством однородности функции Ф по переменным (N1,..., Nn), можно получить соотношение
использование которого в (2.5) приводит к уравнению
Это уравнение, известное как уравнение Гиббса ‑ Дюгема, предложено Дж. Гиббсом (1876 г.), а его приложения в термодинамике растворов рассмотрены П. Дюгемом (1886 г.).
2.2. Дифференциальные уравнения термодинамики
Ценным для практических приложений свойством характеристических функций является следующие из уравнений (2.1) и (2.3) соотношения взаимности для перекрестных производных от обобщенных ТД сил по обобщенным координатам. В самом деле, для функции состояния Z(x1, x2,...) из выражений для ее полного дифференциала
и некоторой пары обобщенных сил
следует соотношение взаимности
Используя равенства (2.11), из уравнения (2.1) и уравнений (2.3) получим соотношения взаимности, называемые уравнениями Максвелла:
Уравнения Максвелла широко используются в термодинамике.
Используя изложенный метод, рассмотрим теоретические основы составления таблиц термодинамических свойств веществ. Пусть необходимо определить энтропию некоторого вещества. Так как энтропия является функцией состояния, то в переменных (p, T)
Рис. 2.1
Используя уравнение Максвелла (2.12.1) и (¶S/¶T)p = Cp/T получим
Полученная формула решает задачу составления таблиц энтропии вещества, так как функции (¶V/¶T)p и Сp могут быть измерены с высокой точностью в благоприятных для измерений изобарических условиях. Проведя аналогичные вычисления для энтальпии H(p, T) и внутренней энергии U(V, T) получим:
|
|||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 154. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . (2.1)
. (2.1) ;
; 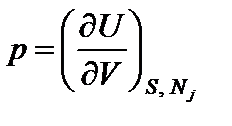 ;
;  . (2.2)
. (2.2)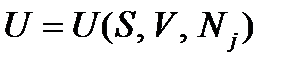 в координатах (S, V, Nj).
в координатах (S, V, Nj).  и
и 
 в координатах (S, p, Nj);
в координатах (S, p, Nj); в координатах (V, T, Nj);
в координатах (V, T, Nj); в координатах (p, T, Nj).
в координатах (p, T, Nj).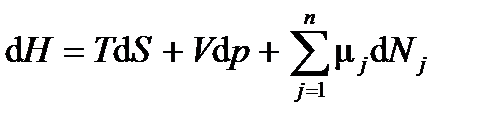 ;
;  ; (2.3)
; (2.3) .
.  ;
;  ;
; 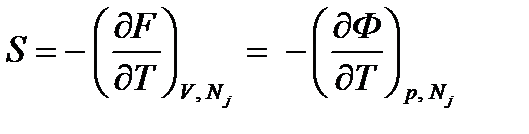 ;
;  ;
;  . (2.4)
. (2.4)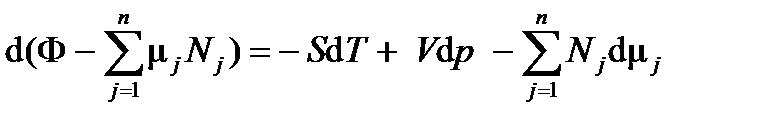 , (2.5)
, (2.5) . (2.6)
. (2.6) . (2.7)
. (2.7) , (2.8)
, (2.8)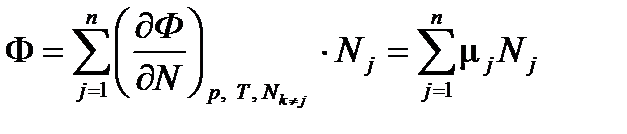 , (2.9)
, (2.9) . (2.10)
. (2.10)
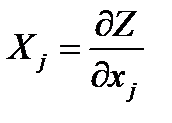 ,
, 
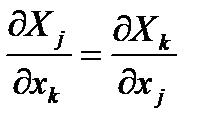 . (2.11)
. (2.11)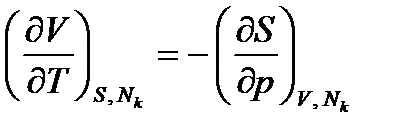 ;
; 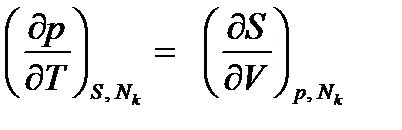 ;
; ;
;  . (2.12.1-4)
. (2.12.1-4) .
.  .
. 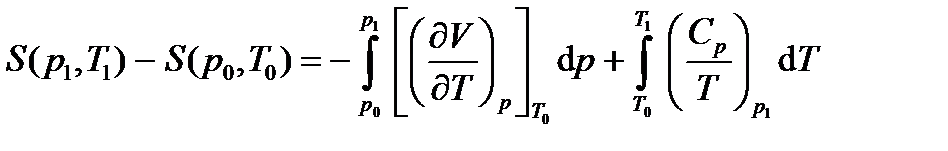 .
.  ;
; 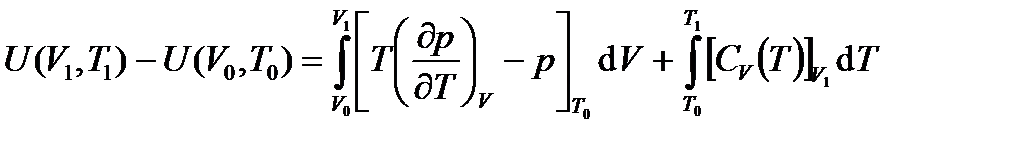 ;
;