
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчет по прочности при действии поперечной силыСтр 1 из 9Следующая ⇒ Расчет плиты по предельным состояниям первой группы. Определение внутренних усилий Конструктивный размер плитыl= 5,5 – 0,2 – 0,02 =5,28 м. Расчетный пролет плиты в соответствии с рис.2: l0 = 5,5 – 0,2 – 0,02 – 0,09 =5,19 м. Поперечное конструктивное сечение приводится к эквивалентному двутавровому сечению cо следующими размерами h=22 см; h0=h-a=22-3=19 cм;h`f = hf=(22-15,9)/2=3,05 см; bf=179 см; b`f=179-3=176 см (рис. 3); nпустот = bпустот = 9 bребра = bребра = 8 Плита рассчитывается как однопролетная шарнирно-опертая балка, загруженная равномерно-распределенной нагрузкой (рис. 4).
Усилия от расчетной полной нагрузки: - изгибающий момент в середине пролета M= - поперечная сила на опорахQ= Усилия от нормативной нагрузки: - полной: Mn = - постоянной и длительной: Mnl =
Расчет прочности плиты по нормальному сечению, при действии изгибающего момента. При расчете прочности расчетное поперечное сечение плиты принимается тавровым с полкой в сжатой зоне (свесы полок в растянутой зоне не учитываются). При расчете принимается вся ширина верхней полкиb`f=176 см, так как верхняя полка по всей ширине плиты соединена с нижней полкой ребрами и
Положение границы сжатой зоны определяется из условия: M≤Mгр= γb1 где M- изгибающий момент в середине пролета от полной нагрузки (g+V); Мгр- момент внутренних сил в нормальном сечении плиты, при условии, что нейтральная ось приходит по нижней грани сжатой полки, т.е. х=h`f;  Rb– расчетное сопротивление бетона сжатию; остальные обозначения приняты в соответствии с рис.3. Если это условие выполняется, граница сжатой зоны проходит в полке, и площадь растянутой арматуры определяется как для прямоугольного сечения шириной b`f. 6579≤0,9 Rb=11,5 МПа=1,15 кН/см2 6579 кН Далее определяем:
По таблице (приложение 10) принимаем
Должно выполняться условие Значение
εs,el - относительная деформация арматуры растянутой зоны, вызванная внешней нагрузкой при достижении в этой арматуре напряжения, равного Rs; εb,ult -относительная деформация сжатого бетона при напряжениях, равных Rb, принимаемая равной 0,0035. Для арматуры с условным пределом текучести значение εs,elопределяется по формуле: εs,el= σ*sp- предварительное напряжение в арматуре с учетом всех потерь и коэффициентом σspпринимается не более 0,9 Принимаем σsp=0,8Rsn=0,8 Полные суммарные потери при проектировании принимаются не менее 100 Мпа, При определении εs,el: σ*sp=0.9 εs,el=
Площадь сечения арматуры: Asp= Rs=520 МПа=52кН/см2 Принимаем 9Æ10 А600 с Аsp=7,07см2 Напрягаемые стержни должны располагаться симметрично и расстояние между ними должно быть не более 400 мм и не более 1,5hпри h>150 мм. Поэтому принимаем 10Æ10 А600 с Аsp=7,85 см2
Расчет по прочности при действии поперечной силы Поперечная сила от полной нагрузки
Расчет предварительно напряженных элементов по сжатой бетонной полосе между наклонными сечениями производят из условия:
Расчет предварительно напряженных изгибаемых элементов по наклонному сечению производят из условия:
Допускается производить расчёт наклонного сечения из условия:
где
Таким образом, бетон не в состоянии воспринять всю поперечную силу в сечении и необходимо установить поперечную арматуру (хомуты) на нагрузку:
Усилие в поперечной арматуре на единицу длины равно:
Назначаем шаг хомутов с учетом требований СП:
Находим требуемую площадь поперечной арматуры:
Принимаем арматуру 4Ø4 В500С: Окончательно принимаем на приопорных участках плиты четыре каркаса с поперечной рабочей арматурой 4Ø4 В500С, расположенной с шагом Sw=10 см. Проверяем прочность сечения:
Так как условие выполняется, то прочность по наклонному сечению обеспечена. |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 696. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ≈ 9 пустот (8 промежуточных ребер и 2 крайних)
≈ 9 пустот (8 промежуточных ребер и 2 крайних) 15,9 = 143,1 см (15,9 см- диаметр пустот)
15,9 = 143,1 см (15,9 см- диаметр пустот)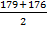 – 143,1= 34,4 см, промежуточные ребра принимаем по 3 см.
– 143,1= 34,4 см, промежуточные ребра принимаем по 3 см. x=5,2 см (х- ширина крайнего ребра)
x=5,2 см (х- ширина крайнего ребра) =65,79 кН
=65,79 кН 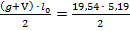 =50,71 кН.
=50,71 кН. =56,13 кН×м;
=56,13 кН×м; =39,46кН×м.
=39,46кН×м. =70,8 <
=70,8 < 

 3,05
3,05  =9709 кН
=9709 кН 
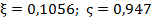
 – относительная высота сжатой зоны бетона.
– относительная высота сжатой зоны бетона.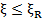 , где
, где  -граничная относительная высота сжатой зоны.
-граничная относительная высота сжатой зоны.

 (коэффициент точности натяжения арматуры)
(коэффициент точности натяжения арматуры) для горячекатаной и термомеханически упрочненной арматуры (А600)и не более 0,8
для горячекатаной и термомеханически упрочненной арматуры (А600)и не более 0,8  МПа
МПа = 0,00294;
= 0,00294; ;
; , условие соблюдается.Высота сжатой зоны x=
, условие соблюдается.Высота сжатой зоны x= 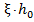 =0,1056
=0,1056  =
=  =7,03см2.
=7,03см2. .
.
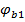 – коэффициент, принимаемый равным 0,3;
– коэффициент, принимаемый равным 0,3; - поперечная сила в нормальном сечении элемента;
- поперечная сила в нормальном сечении элемента;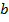 – ширина ребра,
– ширина ребра, 

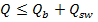
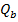 – поперечная сила, воспринимаемая бетоном в наклонном сечении;
– поперечная сила, воспринимаемая бетоном в наклонном сечении;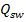 – поперечная сила, воспринимаемая арматурой в наклонном сечении.
– поперечная сила, воспринимаемая арматурой в наклонном сечении. , принимается
, принимается  ;
; – коэффициент, принимаемый равным 1,5;
– коэффициент, принимаемый равным 1,5; ;
; кН.
кН. кН.
кН.

 ;
; 
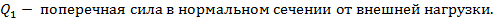




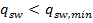



 ,
, кН;
кН;