
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ ⇐ ПредыдущаяСтр 2 из 2 1 Метелева, Д. Н. Применении игровых технологий при изучении темы «Числовые последовательности. Прогрессии» // Образование и наука в современных реалиях : Сборник материалов III Международной научно-практической конференции. 2017. С. 109-111. 2
ПРИЛОЖЕНИЯ Приложение А. Логико-дидактический анализ теоретического материала темы по учебнику «Алгебра» под ред. Ш. А. Алимова Параграф 27 «Числовая последовательность» а) Каким понятиям в теме даются формально-логические определения, а какие вводятся описательно? В параграфе «Числовая последовательность» понятие числовая последовательность вводится описательно (последовательность, в которой каждому натуральному числу n ставится в соответствие число an). Вводятся понятия бесконечной числовой последовательности и членов этой последовательности (нет четкого определения): а1 – первый член последовательности, а2 – второй член последовательности и т. д., аn – n-ый член последовательности, аn+1 – n+1-ый член последовательности и т. д. Вводятся два способа задания последовательности: с помощью формулы ее n-го члена и рекуррентный способ. Понятие рекуррентного способа задания последовательности вводится описательно (это такой способ задания последовательности, при котором последовательность задается формулой, позволяющей вычислить (n+1)-ый член последовательности через предыдущие n членов, некоторые из которых задаются дополнительно). б) Какие понятия темы являются ведущими? Ведущим понятием в данной теме является понятие числовой последовательности. На этом понятии основаны понятия арифметической и геометрической прогрессий.  в) Как они связаны с предшествующим содержанием? Какие методологические знания характеризуют ведущие понятия темы (новизна видов, их определений, логических структур, наличие кванторов)? Ранее в курсе алгебры учащиеся не встречались с понятием числовой последовательности. Этот материал является новым для них. Структура введения понятия числовой последовательности не является новой. Определение числовой последовательности описательное. Кванторы отсутствуют. г) Какие теоремы дополняют содержание понятий, данное в определениях (свойства, признаки, существование)? д) Каковы общелогические и специфические методы и приемы доказательств теорем? Какова их новизна для учащихся? е) Какие методологические знания можно формировать у школьников на этапах «открытия» формулировок теорем и поиска доказательств теорем? ж) Выделены ли в тексте нужные правила, определяющие способы деятельности? Следует ли им давать алгоритмическое описание? г)- ж) В параграфе «Числовая последовательность» теоремы не приведены. Параграф 28 «Арифметическая прогрессия» а) Каким понятиям в теме даются формально-логические определения, а какие вводятся описательно? В параграфе «Арифметическая прогрессия» вводится понятие арифметическая прогрессия: «Числовая последовательность a1, a2, a3,…,an,… называется арифметической прогрессией, если для всех натуральных n выполняется равенство an+1=an+d, где d - некоторое число» (формально-логическое, через род и видовые отличия, родовое понятие – числовая последовательность a1, a2, a3,…,an,…, видовое отличие задается индуктивно). Понятие разности арифметической прогрессии вводится символьной записью: d=an+1 - an. б) Какие понятия темы являются ведущими? Ведущим понятием в данной теме является понятие арифметической прогрессии. На данном понятии основаны решения простейших заданий, доказательство свойства арифметической прогрессии о среднем арифметическом, выведение формулы n-го члена арифметической прогрессии, а также последующий материал данной главы, а именно доказательство теоремы о сумме n первых членов арифметической прогрессии, приведенное в параграфе 29 «Сумма n первых членов арифметической прогрессии». в) Как они связаны с предшествующим содержанием? Какие методологические знания характеризуют ведущие понятия темы (новизна видов, их определений, логических структур, наличие кванторов)? Ранее в курсе алгебры учащиеся не встречались с понятием арифметической прогрессии. Этот материал является новым для них. Структура введения понятия арифметической прогрессии также является новой, так как впервые видовое отличие задается индуктивно. Кванторы отсутствуют. г) Какие теоремы дополняют содержание понятий, данное в определениях (свойства, признаки, существование)? Содержание понятия арифметической прогрессии дополняют свойство арифметической прогрессии о среднем арифметическом: «Каждый член арифметической прогрессии а1, а2, а3,…,аn,…, начиная со второго, равен среднему арифметическому двух соседних с ним членов: д) Каковы общелогические и специфические методы и приемы доказательств теорем? Какова их новизна для учащихся? Доказательство свойства арифметической прогрессии о среднем арифметическом не является для учащихся новым, доказательство осуществляется на основе определения арифметической прогрессии и с помощью алгебраических действий. Свойство арифметической прогрессии о среднем арифметическом доказывается следующим методом: выражаются предыдущий и последующий члены через n-ый член, затем складываются полученные равенства, далее выражается n-ый член. Выведение формулы n-го члена арифметической прогрессии основывается на определении арифметической прогрессии и осуществляется методом неполной индукции, что является для учащихся новым. е) Какие методологические знания можно формировать у школьников на этапах «открытия» формулировок теорем и поиска доказательств теорем? Свойство арифметической прогрессии о среднем арифметическом и формула n-го члена арифметической прогрессии доказываются на основе определения арифметической прогрессии, то есть с помощью рекуррентной формулы an+1=an+d, поэтому можно формировать у учащихся умения применять рекуррентную формулу для доказательства теорем. ж) Выделены ли в тексте нужные правила, определяющие способы деятельности? Следует ли им давать алгоритмическое описание? В тексте нужные правила не выделены, но проводя эвристическую беседу с учащимися, можно приарифметическом и выведению формулы n-го члена арифметической прогрессии. Учащимся известно только определение арифметической прогрессии. Следовательно, учащимся может быть предложено получить доказательство свойства арифметической прогрессии о среднем арифметическом и вывести формулу n-го члена арифметической прогрессии, используя определение арифметической прогрессии, то есть рекуррентную формулу. Алгоритмическое описание действий давать не обязательно, поскольку доказательство является несложным. Параграф 29 «Сумма n первых членов арифметической прогрессии» а) Каким понятиям в теме даются формально-логические определения, а какие вводятся описательно? В параграфе «Сумма n первых членов арифметической прогрессии» вводится понятие суммы n первых членов арифметической прогрессии в символьной записи: б) Какие понятия темы являются ведущими? Ведущим понятием в данной теме является понятие суммы n первых членов арифметической прогрессии. На данном понятии основано доказательство теоремы о сумме n первых членов арифметической прогрессии. в) Как они связаны с предшествующим содержанием? Какие методологические знания характеризуют ведущие понятия темы (новизна видов, их определений, логических структур, наличие кванторов)? Ранее в курсе алгебры учащиеся не встречались с понятием суммы n первых членов арифметической прогрессии. Этот материал является новым для них. Понятие суммы n первых членов арифметической прогрессии вводится символьной записью, что не является новым для учащихся. Кванторы отсутствуют. г) Какие теоремы дополняют содержание понятий, данное в определениях (свойства, признаки, существование)? Содержание понятия суммы n первых членов арифметической прогрессии дополняет теорема о сумме n первых членов арифметической прогрессии: «Сумма n первых членов арифметической прогрессии равна д) Каковы общелогические и специфические методы и приемы доказательств теорем? Какова их новизна для учащихся? Для доказательства теоремы о сумме n первых членов арифметической прогрессии используются понятие суммы n первых членов арифметической прогрессии, определение арифметической прогрессии и равносильные преобразования. Данное доказательство осуществляется синтетическим методом, что не является для учащихся новым. Для доказательства теоремы о сумме n первых членов арифметической прогрессии используется следующий прием: записывают эту сумму дважды, расположив в первом случае слагаемые в порядке возрастания их номеров, а во втором случае в порядке убывания одна под другой. Получают, что сумма каждой пары членов прогрессии, расположенные друг под другом, равна (a1 + an). В итоге, сложив почленно выражения и выполнив преобразования, получают нужную формулу. е) Какие методологические знания можно формировать у школьников на этапах «открытия» формулировок теорем и поиска доказательств теорем? Теорема о сумме n первых членов арифметической прогрессии доказывается синтетическим методом, поэтому можно формировать у учащихся умения доказывать теоремы данным методом. ж) Выделены ли в тексте нужные правила, определяющие способы деятельности? Следует ли им давать алгоритмическое описание? В тексте нужные правила выделены. Алгоритмическое описание действий давать не обязательно, поскольку доказательство является несложным. Параграф 30 «Геометрическая прогрессия» а) Каким понятиям в теме даются формально-логические определения, а какие вводятся описательно? В параграфе «Геометрическая прогрессия» вводится понятие геометрическая прогрессия: «Числовая последовательность b1, b2, b3,…,bn,… называется геометрической прогрессией, если для всех натуральных n выполняется равенство bn+1=bn×q, где bn ≠ 0, q – некоторое число, не равное нулю» (формально-логическое, через род и видовые отличия, родовое понятие – числовая последовательность b1, b2, b3,…,bn,…, видовое отличие задается индуктивно). Понятие знаменателя геометрической прогрессии вводится символьной записью: б) Какие понятия темы являются ведущими? Ведущим понятием в данной теме является понятие геометрической прогрессии. На данном понятии основаны решения простейших заданий, доказательство свойства геометрической прогрессии о среднем геометрическом, выведение формулы n-го члена геометрической прогрессии, а также последующий материал данной главы, а именно доказательство теоремы о сумме n первых членов геометрической прогрессии со знаменателем q≠1, приведенное в параграфе 31 «Сумма n первых членов геометрической прогрессии». в) Как они связаны с предшествующим содержанием? Какие методологические знания характеризуют ведущие понятия темы (новизна видов, их определений, логических структур, наличие кванторов)? Ранее в курсе алгебры учащиеся не встречались с понятием геометрической прогрессии. Этот материал является новым для них. Но понятие геометрической прогрессии является аналогичным понятию арифметической прогрессии, поэтому структура введения понятия геометрической прогрессии уже не является новой для учащихся. Кванторы в определении отсутствуют. г) Какие теоремы дополняют содержание понятий, данное в определениях (свойства, признаки, существование)? Содержание понятия геометрической прогрессии дополняют свойство геометрической прогрессии о среднем геометрическом: «Каждый член геометрической прогрессии b1, b2, b3,…,bn,…, начиная со второго, равен среднему геометрическому двух соседних с ним членов: д) Каковы обще логические и специфические методы и приемы доказательств теорем? Какова их новизна для учащихся? Доказательство свойства геометрической прогрессии о среднем геометрическом не является для учащихся новым, оно является аналогичным доказательству свойства арифметической прогрессии о среднем арифметическом и осуществляется на основе определения геометрической прогрессии и с помощью алгебраических действий. Свойство геометрической прогрессии о среднем геометрическом доказывается следующим методом: выражаются предыдущий и последующий члены через n-ый член, затем умножаются полученные равенства, далее выражается n-ый член. Выведение формулы n-го члена геометрической прогрессии является аналогичным выведению формулы n-го члена арифметической прогрессии, оно основывается на определении геометрической прогрессии и осуществляется методом неполной индукции, что также уже не является новым для учащихся, так как таким же методом выводится формулы n-го члена арифметической прогрессии. е) Какие методологические знания можно формировать у школьников на этапах «открытия» формулировок теорем и поиска доказательств теорем? Свойство геометрической прогрессии о среднем геометрическом и формула n-го члена геометрической прогрессии доказываются на основе определения геометрической прогрессии, то есть с помощью рекуррентной формулы bn+1=bn*q, bn≠0, q≠0, поэтому можно формировать у учащихся умения применять рекуррентную формулу для доказательства теорем. ж) Выделены ли в тексте нужные правила, определяющие способы деятельности? Следует ли им давать алгоритмическое описание? В тексте нужные правила не выделены, но проводя эвристическую беседу с учащимися, можно прийти к доказательству свойства геометрической прогрессии о среднем геометрической и выведению формулы n-го члена геометрической прогрессии. Учащимся известно только определение геометрической прогрессии. Следовательно, учащимся может быть предложено получить доказательство свойства геометрической прогрессии о среднем геометрическом и вывести формулу n-го члена геометрической прогрессии, используя определение геометрической прогрессии, то есть рекуррентную формулу. Алгоритмическое описание действий давать не обязательно, поскольку доказательство является несложным. Параграф 31 «Сумма n первых членов геометрической прогрессии» а) Каким понятиям в теме даются формально-логические определения, а какие вводятся описательно? В параграфе «Сумма n первых членов геометрической прогрессии» вводится понятие суммы n первых членов геометрической прогрессии со знаменателем q≠1 в символьной записи: б) Какие понятия темы являются ведущими? Ведущим понятием в данной теме является понятие суммы n первых членов геометрической прогрессии со знаменателем q≠1. На данном понятии основано доказательство теоремы о сумме n первых членов геометрической прогрессии со знаменателем q≠1. в) Как они связаны с предшествующим содержанием? Какие методологические знания характеризуют ведущие понятия темы (новизна видов, их определений, логических структур, наличие кванторов)? Ранее в курсе алгебры учащиеся не встречались с понятием суммы n первых членов геометрической прогрессии со знаменателем q≠1. Этот материал является новым для них. Но понятие суммы n первых членов геометрической прогрессии со знаменателем q≠1 является аналогичным для понятия суммы n первых членов арифметической прогрессии. Понятие суммы n первых членов геометрической прогрессии со знаменателем q≠1 вводится символьной записью. Кванторы в определении отсутствуют. г) Какие теоремы дополняют содержание понятий, данное в определениях (свойства, признаки, существование)? Содержание понятия суммы n первых членов геометрической прогрессии со знаменателем q≠1 дополняет теорема о сумме n первых членов геометрической прогрессии со знаменателем q≠1: «Сумма n первых членов геометрической прогрессии со знаменателем q≠1 равна д) Каковы общелогические и специфические методы и приемы доказательств теорем? Какова их новизна для учащихся? Для доказательства теоремы о сумме n первых членов геометрической прогрессии со знаменателем q≠1 используются понятие суммы n первых членов геометрической прогрессии со знаменателем q≠1, определение геометрической прогрессии и равносильные преобразования. Данное доказательство является аналогичным доказательству теоремы о сумме n первых членов арифметической прогрессии и осуществляется также синтетическим методом, что не является для учащихся новым. Для доказательства теоремы о сумме n первых членов геометрической прогрессии со знаменателем q≠1 используется следующий прием: записывают эту сумму дважды, в первом случае все члены записываются по формуле n-ого члена, а во втором случае всю сумму умножают на знаменатель. Затем из первого выражения вычитают второе и выражают сумму прогрессии через первый член и знаменатель прогрессии. е) Какие методологические знания можно формировать у школьников на этапах «открытия» формулировок теорем и поиска доказательств теорем? Теорема о сумме n первых членов геометрической прогрессии со знаменателем q≠1 доказывается синтетическим методом, поэтому можно формировать у учащихся умения доказывать теоремы данным методом. ж) Выделены ли в тексте нужные правила, определяющие способы деятельности? Следует ли им давать алгоритмическое описание? Основные дидактические единицы темы: понятие числовой последовательности, определения понятий арифметической и геометрической прогрессий, формулы n-го члена арифметической и геометрической прогрессий, свойства арифметической прогрессии о среднем арифметическом и геометрической прогрессии о среднем геометрическом, формулы суммы n первых членов арифметической и геометрической прогрессий, определение понятия бесконечно убывающей геометрической прогрессии, формула суммы бесконечно убывающей геометрической прогрессии. Нет четкого определения понятия числовой последовательности. Числовая последовательность определяется способом задания. Выделяют два способа задания последовательности: с помощью формулы n-го члена и рекуррентный способ. Определения арифметической и геометрической прогрессий вводятся аналогично. Прогрессиям дается формально-логическое определение: родовое понятие – числовая последовательность, видовое отличие задается индуктивно. Учащиеся впервые встречаются с определениями такого вида. Для иллюстрации нужно привести историческую справку или пример из жизни, что может послужить мотивацией для изучения данной темы. Определить то, что между членами прогрессий есть зависимость, и какая это зависимость, могут сами ученики (нужно привести наглядный пример каждой прогрессии). Учащиеся смогут самостоятельно сформулировать определения прогрессий, зная, что они являются числовыми последовательностями, и определив предварительно зависимость между членами каждой из них. Кроме словесной формулировки необходимо рассмотреть и символическую запись определений, т. к. в ней отражены рекуррентные формулы, задающие прогрессии. В рассматриваемом учебнике символические записи определений имеются. Особо выделяется из-за большого прикладного значения бесконечно убывающая геометрическая прогрессия, как частный случай геометрической прогрессии, у которой модуль знаменателя меньше 1. И для бесконечно убывающей геометрической прогрессии существует формула ее суммы. Кроме определений также являются аналогичными свойства арифметической и геометрической прогрессий и их доказательства, формулы n-го члена прогрессий и способы их выведения, теоремы о сумме n первых членов прогрессий и их доказательства. Даже соответствующие задачи в тексте параграфов (ключевые) имеют аналогичные решения. Для арифметической прогрессии выполняется свойство о среднем арифметическом. Для геометрической прогрессии выполняется аналогичное, но о среднем геометрическом. Они доказываются следующим методом: выражаются предыдущий и последующий члены через n-ый член, затем складываются (для арифметической прогрессии) / умножаются (для геометрической прогрессии) полученные равенства, далее выражается n-ый член. То есть и доказательства этих свойств аналогичны. Из этих свойств вытекают названия «арифметическая прогрессия» и «геометрическая прогрессия». Учитель должен на это обратить внимание учеников. Важно учителю также отметить, что для каждого из этих свойств справедливо обратное утверждение, то есть можно сформулировать признак, а тогда можно сформулировать и критерий, который будем называть характеристическим свойством арифметической прогрессии и характеристическим свойством геометрической прогрессии. В учебнике приведены только свойства, поэтому учителю необходимо в совместной деятельности с учащимися сформулировать признаки и критерии для арифметической и геометрической прогрессий. Для арифметической и геометрической прогрессий также аналогично выводятся формулы n-ого члена методом неполной индукции, в которых n-ый член находится через первый член и разность для арифметической / знаменатель для геометрической прогрессии. Эти формулы являются ещё одним способом задания прогрессии. Вообще в математике эти формулы можно доказать с помощью метода математической индукции, но он достаточно сложен для восприятия школьников, поэтому данные формулы приведены в рассматриваемом учебнике без доказательства. Теоремы о суммах n первых членов арифметической и геометрической прогрессий доказываются синтетическим методом. Для доказательства теоремы о сумме n первых членов арифметической прогрессии используется следующий прием: записывают эту сумму дважды, расположив в первом случае слагаемые в порядке возрастания их номеров, а во втором случае в порядке убывания одна под другой. Получают, что сумма каждой пары членов прогрессии, расположенные друг под другом, равна (a1 + an). В итоге, сложив почленно выражения и выполнив преобразования, получают нужную формулу. Для геометрической прогрессии также записывается сумма в двух случаях: в первом все члены записываются по формуле n-ого члена, во втором всю сумму умножают на знаменатель. Затем из первого выражения вычитают второе и выражают сумму прогрессии через первый член и знаменатель прогрессии. Итак, приемы доказательства этих теорем также аналогичны. Также задачи, приведенные в данной теме с решением в тексте параграфов, являются аналогичными. Правила решения подобных задач не сформулированы. Учитель может их выделить совместно с учениками (чтобы найти требуемое в задаче, можно выписать соответствующую формулу, определить, что в ней известно, а что нет, затем выразить из этой формулы то, что нужно найти, подставив известные значения).
Приложение Б. Анализ задачного материала темы «Прогрессии» в учебнике «Алгебра» под ред. Ш. А. Алимова Задачный материал присутствует как в параграфах§§27-32, так и в упражнения в главе, а также задачах на повторение курса алгебры за 9 класс. Представлены задачи на отработку основных дидактических единиц. Параграф 27 «Числовая последовательность» Дана последовательность: а) указать номер заданного члена последовательности: 361(2) б) назвать член под заданным номером: 361(1) Дана формула n-го члена последовательности а) вычислить заданное число членов: 362, 446 б) выяснить, является ли число членом данной последовательности: 363, 364, 503, 691 в) указать номер заданного члена последовательности: задача 2, 366, г) назвать член последовательности под заданным номером: задача 1,370, 447 Дана рекуррентная формула и условие, вычислить заданное число членов последовательности: задача 3, 365, 367, 368, 369, 448, 461, 504, 505, 692 Параграф 28 «Арифметическая прогрессия» Дана прогрессия а) найти разность и первый член: 371,449 б) записать формулу n-го члена 375 в) выяснить, является ли число членом данной прогрессии: 377, 378, г) указать номер заданного члена прогрессии: задача 3, 376, 378,383,384 Текстовые задачи: 386-387, 475, 482, 529, 530, 535, 543, 712 Доказать равенство: 388-389 На формулу n-го члена:
1)Дана формула n-го члена, доказать, что последовательность является арифметической прогрессией: задача 1, задача 5 (текстовая на характеристическое свойство), 373, 450, 508 2) Дана разность и первый член арифметической прогрессии: а) найти заданное число членов данной прогрессии: 372 б) найти член с заданным номером: задача 2, 374, 451, 506 3)Даны несколько членов арифметической прогрессии. а) найти формулу n-го члена: задача 4, 382 б) найти разность: 379, 385 (на характеристическое свойство), 462, 693, 700 в) найти первый член прогрессии: 381(2), 700 г) записать заданное число членов прогрессии: 463, 465 д) найти член с заданным номером: 696, 701 4)Дана разность и член с заданным номером. Найти первый член прогрессии: 380, 381(1), 694 На характеристическое свойство: а) вставить число, чтобы получилась прогрессия: 464, 466 б) показать, что три числа образуют прогрессию: 467, 712 Параграф 29 «Сумма n первых членов арифметической прогрессии» На формулу суммы n первых членов 1) Найти сумму n первых членов арифметической прогрессии: а) даны первый член и разность: 393 б) дана сумма нескольких членов (не соседних): 403 в) даны первый член и член под заданным номером: задача 1, 390, 391, 392, 452, 453, 507, 531 г) дана прогрессия: задача 3, 394, 395, 454 д) дана формула n-го члена: задача 2, 396(неявно), 397 е) последовательность задана рекуррентной формулой 398 2) Найти n-ый (первый) член и разность по первому(n-му) члену и сумме первых n членов: 400, 401, 469, 476 (дана сумма n первых и их произведение), 477, 702 3) Сколько нужно взять чисел из промежутка, чтобы получить заданную сумму: задача 4, 399, 468 4) Найти первый член и разность по двум суммам: 404 Текстовые задачи: 402, 478 Доказать равенство: 405, 544 Параграф 30 «Геометрическая прогрессия» Доказать, что последовательность является геометрической прогрессией: задача 1, задача 5 (текст), 408, 419 (текст), 703 Дан знаменатель и первый член прогрессии: а) найти член с заданным номером (первый): задача 2, 409, 457, 470 б) записать заданное количество членов прогрессии: 407 Даны два члена прогрессии: а) записать формулу n-го члена: задача 4, 410, 705 б) найти член под заданным номером: 412, 414, 415, 471, 510, 698, 706, 709 Текстовые задачи: 417-418, 481, 483, 532, 543, 714 Дана прогрессия а) найти знаменатель и первый член: 406, 455 б) записать формулу n-го члена: задача 4, 410, 456 в) найти номер заданного члена прогрессии: задача 3, 411,413 г) найти член под заданным номером: 413, 455 На характеристическое свойство: а) вставить число, чтобы получилась прогрессия: 472, 707 б) показать. Что три числа образуют прогрессию: 713 Параграф 31 «Сумма n первых членов геометрической прогрессии» На формулу суммы n первых членов 1) Найти сумму n первых членов арифметической прогрессии: а) даны первый член и знамена, 458, 510, 511 б) даны несколько членов: 426 (плюс найти еще один член под заданным номером), 430(3,4), 710 (1, 3.4) в) дана прогрессия: задача 2, задача 5, 421, 425,459, 699 г) дана формула n-го члена: 427 д) дана рекуррентная формула: 697 2) Найти n по знаменателю, первому(n-му) члену и сумме первых n членов: задача 4, 423,424 3) Дан знаменатель и сумма n первых членов, найти первый (n-ый) член: задача 3, 422, 429(дан n-ый член вместо знаменателя), 533, 704, 708, 710 (2) 4) Найти знаменатель 2) Доказать равенство: 428, 479, 480. Выводы из анализа задачного материала Задачи, рассматриваемые в главе «Прогрессии» отличаются многообразием своих разновидностей. Расположение в параграфах от простых к сложным. Упражнения позволяют отработать все представленные дидактические единицы главы. На отработку некоторых типов задач представленных в учебнике номеров недостаточно. Мало упражнений на отработку характеристического свойства арифметической прогрессии и характеристического свойства геометрической прогрессии, поэтому задачный материал в учебнике можно дополнить задачами такого вида. Комбинированных задач на арифметическую и геометрическую прогрессии не выявлено (только в упражнениях для самостоятельной работы). Поэтому нужно дополнить материал задачами данного типа. Например, следующими: Задача 1. Три числа, сумма которых равна 78, образуют возрастающую геометрическую прогрессии. Их же можно рассматривать как первый, третий и девятый члены арифметической прогрессии. Найти большее число. Задача 2. Три числа являются первым, вторым и третьим членов арифметической прогрессии и, соответственно, первым, третьим и вторым членами геометрической прогрессии. Найдите эти числа, если известно, что сумма квадрата первого из них, удвоенного второго и утроенного третьего равна . Задача 3. Сумма трех чисел, образующих арифметическую прогрессию, равна 21. Если к этим числам прибавить соответственно 2, 3, 9, то полученные числа образуют геометрическую прогрессию. Найти указанные числа. Задача 4. В геометрической прогрессии второй член равен 8, а пятый - 512. Составить арифметическую прогрессию, у которой разность в два раза меньше знаменателя геометрической прогрессии, а суммы трех первых членов в одной и другой прогрессиях были бы равны. Задача 5. Пять различных чисел являются последовательными членами арифметической прогрессии. Если удалить ее 2-й и 3-й члены, то оставшиеся числа будут последовательными членами геометрической прогрессии. Найти ее знаменатель. В теме «Прогрессии» вводится достаточно большое количество формул. Каждая из этих формул порождает целую систему упражнений. Так как темы арифметическая и геометрическая прогрессия рассматриваются аналогично, то и группы задач на каждую из формул для арифметической прогрессии имеют аналогичную группу задач на аналогичную формулу для геометрической прогрессии. Рассмотрим группы задач, порождаемых формулами для геометрической и арифметической прогрессий.
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 338. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 » и формула n-го члена арифметической прогрессии: аn=a1+(n-1)d.
» и формула n-го члена арифметической прогрессии: аn=a1+(n-1)d.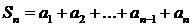 .
. ».
». .
. , bi>0 , n>1» и формула n-го члена геометрической прогрессии:
, bi>0 , n>1» и формула n-го члена геометрической прогрессии:  .
. .
. ».
».