
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Эта формула, называется формулой Муавра.Стр 1 из 2Следующая ⇒ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Московский государственный университет Приборостроения и информатики
Кафедра высшей математики Комплексные числа (решение задач) Учебное пособие для студентов всех форм обучения для самостоятельной подготовки к выполнению контрольных работ.
Москва 2005
Составитель: к.ф.м.н., доцент Выборнов А.Н..
В пособии кратко приведены основные теоретические сведения по теме «комплексные числа» (не заменяют лекционный материал или материал учебника), разобраны некоторые задачи. Пособие составлено на основе пособия МГУПИ для заочного отделения (авторы: Баланкина Е.С., Головешкин В.А., Каримова Н.А., Меренкова Т.В., Соркина Л.И., Якобовская И.М.). Пособие может использоваться как дополнительное пособие по развитию навыков решения задач.
В алгебраической форме комплексное число z представляется в виде
Комплексные числа удобно представлять точками на плоскости по правилу: комплексному числу
 Два комплексных числа
Операции сложения (вычитания) для комплексных чисел определены следующим образом: Любое действительное число Операция умножения
Так как
Деление комплексных чисел осуществляется по следующей схеме (числитель и знаменатель умножают на сопряженное к знаменателю):
Пример. Вычислить Решение.
=
Пример. Вычислить
=
Тригонометрическая форма комплексного числа. Обозначим Угол наклона вектора Представление комплексного числа в виде Для комплексных чисел, заданных в тригонометрической форме, операции умножения и деления выполняются достаточно просто. Пусть Тогда:
( при умножении комплексных чисел модули перемножаются, а аргументы складываются);
(при делении комплексных чисел модули делятся, а аргументы вычитаются). Из формулы умножения комплексных чисел, заданных в тригонометрической форме следует, что если
Эта формула, называется формулой Муавра. Если комплексное число задано в тригонометрической форме Если комплексное число представлено в алгебраической форме
Согласно формуле Эйлера Следовательно, комплексное число |
|||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 134. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


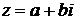 , где
, где 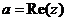 - действительная часть,
- действительная часть,  - мнимая часть, число
- мнимая часть, число 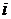 - мнимая единица, обладающая свойством
- мнимая единица, обладающая свойством 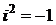 .
.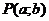 . Получается взаимно однозначное соответствие между всеми точками плоскости и всеми комплексными числами. Действительные числа при этом образуют ось абсцисс, поэтому ее называют действительной осью на комплексной плоскости, ось ординат называют мнимой осью – она состоит из комплексных чисел с нулевой действительной частью.
. Получается взаимно однозначное соответствие между всеми точками плоскости и всеми комплексными числами. Действительные числа при этом образуют ось абсцисс, поэтому ее называют действительной осью на комплексной плоскости, ось ординат называют мнимой осью – она состоит из комплексных чисел с нулевой действительной частью.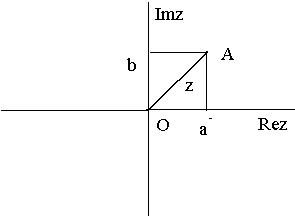
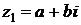 и
и 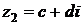 считаются равными тогда и только тогда, когда равны их действительные и мнимые части. То есть
считаются равными тогда и только тогда, когда равны их действительные и мнимые части. То есть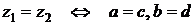 .
.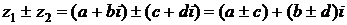 , то есть отдельно складываются (вычитаются) действительные и мнимые части.
, то есть отдельно складываются (вычитаются) действительные и мнимые части.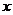 может рассматриваться как комплексное, если отождествить
может рассматриваться как комплексное, если отождествить 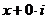 .
.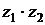 проводится по следующей схеме
проводится по следующей схеме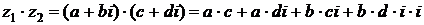
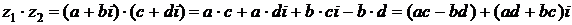
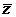 , где
, где 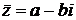 . Заметим, что
. Заметим, что 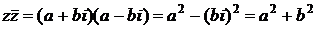 .
.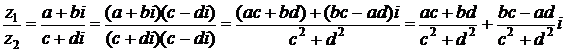
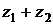 ,
, 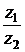 , если
, если 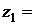
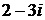 ,
, 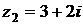 .
.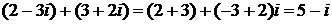 .
.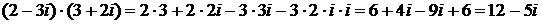
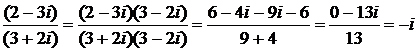 .
.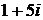 ,
, 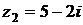
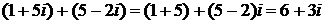
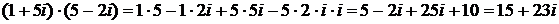
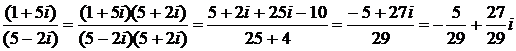
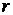 - модуль вектора
- модуль вектора 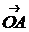 ,
, 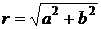 . Это число назовем модулем
. Это число назовем модулем 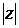 - комплексного числа
- комплексного числа 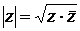 .
.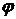 и назовем аргументом комплексного числа z. Тогда
и назовем аргументом комплексного числа z. Тогда 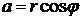 ,
, 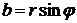 . Следовательно,
. Следовательно, 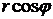 +
+ 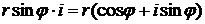 .
.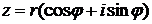 называется тригонометрической формой комплексного числа. Заметим, что аргумент комплексного числа определен с точностью до слагаемого, кратного
называется тригонометрической формой комплексного числа. Заметим, что аргумент комплексного числа определен с точностью до слагаемого, кратного 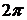 . Если не будет специальных оговорок, мы будем предполагать, что речь идет о главном значении аргумента
. Если не будет специальных оговорок, мы будем предполагать, что речь идет о главном значении аргумента 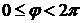 . В общем случае два комплексных числа
. В общем случае два комплексных числа 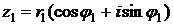 и
и 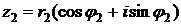 равны, когда равны их модули, а аргументы отличаются на слагаемое, кратное
равны, когда равны их модули, а аргументы отличаются на слагаемое, кратное 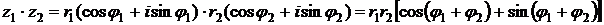
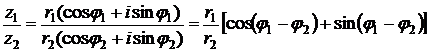
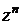 , где n – целое число равно
, где n – целое число равно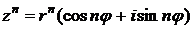
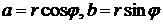 .
.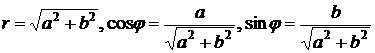 . Известные значения синуса и косинуса однозначно определяют главное значение аргумента.
. Известные значения синуса и косинуса однозначно определяют главное значение аргумента.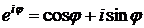 .
.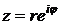 .
.