
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Послідовність графічного інтегрування.1. Ділимо задану криву (рис. 2.7, а) на інтервали - точки 1, 2, 3,…на осі абсцис. Рис. 2.7 2. Проводимо полюсну відстань ОР. Ординати 1/, 2/, 3,/…середини кожного інтервалу проектують на вісь ординат і отримані точки з’єднують з полюсом Р. 3. Під діаграмою швидкості будуємо нову систему координат (рис. 2.7, б). Ділимо вісь абсцис на такі ж інтервали, як і на попередньому графіку. 4. З початку нової системи координат 0 проводять у першому інтервалі лінію 0а паралельно до променя Р1; з кінця відрізка 0а проводять у другому інтервалі відрізок ав паралельний променю Р2, і так далі, bc//Р3, сd//Р4,... Отриману ламану лінію замінюють плавною кривою, одержують графік переміщень Масштаб одержаної інтегральної кривої знаходять за формулою
або, в загальному випадку, Чисельне диференціювання та інтегрування.До чисельного диференціювання звертаються, перш за все, коли функція Розглянемо як приклад формули диференціювання функції
Зазначимо, що чисельне диференціювання чутливе до помилок, які викликані похибками вихідних даних. Чисельне інтегрування функції 
Метод планів швидкостей та прискорень Методи графічного диференціювання та інтегрування при всій їх простоті та наочності не розв’язують повністю питання кінематики. Діаграми переміщень, швидкостей та прискорень дають лише скалярні кінематичні величини, а напрями векторів цих величин невідомі. Цього недоліку позбавлений графоаналітичний метод, що ґрунтується на побудові планів швидкостей та прискорень (векторний спосіб); метод достатньою мірою розроблений, точний і зручний у практичному застосуванні, особливо, коли треба визначити швидкості і прискорення для конкретного положення механізму. Теоретичні основи побудови планів швидкостей і прискорень розглядаються в курсі теоретичної механіки. За основу цього методу взята можливість розкласти складний рух точки або ланки на прості рухи шляхом введення додаткової (рухомої) системи відліку. Залежності між кінематичними характеристиками абсолютного, переносного та відносного рухів точки (ланки) записуються у векторній формі та представляються у вигляді планів швидкостей та прискорень. Плани викреслюються у відповідних масштабах, що дозволяє отримати числові значення кінематичних характеристик. Планом швидкостей (прискорень) механізму називають креслення, на якому зображені у вигляді напрямлених відрізків вектори, які у масштабі визначають модуль та напрям швидкостей (прискорень) різних точок ланок для даного положення механізму. План швидкостей (прискорень) механізму є сукупністю планів швидкостей (прискорень) окремих ланок, що побудовані з одного полюса, спільного для всі ланок. Кінематичний аналіз механізму проводиться у такому порядку: - спочатку визначаються кінематичні параметри початкової ланки; - далі виконується кінематичне дослідження окремих структурних груп Ассура в послідовності їх приєднання до початкової ланки при утворенні механізму. При цьому, кожна ланка механізму розглядається як така, що здійснює плоский рух; необхідно визначити швидкість і прискорення щонайменше двох її точок. Цими точками є центри шарнірів обертальних пар і однойменні точки елементів поступальних кінематичних пар. Як сказано, побудова планів виконується за структурними групами в порядку їх приєднання, починаючи з початкової ланки. У цьому випадку у кожній групі Ассура будуть відомі швидкості та прискорення зовнішніх кінематичних пар, якими приєднується дана група. Дослідження кожної групи повинно розпочинатись з визначення кінематичних параметрів внутрішньої пари, яка є спільною для ланок, що утворюють цю пару. Потім, за потреби, визначаються кінематичні параметри інших характерних точок групи та кутові швидкості і прискорення ланок. При кінематичному аналізі механізму спочатку будується план швидкостей, а потім план прискорень. Плани швидкостей початкової ланки. Зазвичай, початкова ланка механізму здійснює обертальний рух (рис. 2.8, а). Швидкість
Рис. 2.8 Відмітимо, що зображення точок ланок (для розглядуваного прикладу О, S, A) на плані швидкостей позначаються малими літерами (о, s, а). Плани прискорень початкової ланки. На рис. 2.8, в, зображений план прискорень початкової ланки. Він побудований за відомими співвідношеннями: - повне прискорення т. А при обертальному русі ланки дорівнює геометричній сумі нормального і дотичного (тангенціального) прискорень, - модуль нормального прискорення т. А: - модуль дотичного прискорення т. А: Масштаб плану прискорень визначається за формулою Вектор дотичного прискорення напрямлений по дотичній до траєкторії руху (перпендикулярно радіусу обертання) в бік напрямку кутового прискорення Відзначимо, що переважно в задачах кінематики приймається, що початкова ланка обертається рівномірно ( Плани швидкостей та прискорень при складному русі ланки. Складним рухом ланки (точки) називається такий рух, при якому ланка одночасно бере участь у двох або більше простих рухах. Рух, що здійснює ланка (точка) по відношенню до рухомої системи відліку, називається відносним рухом. Рух, що здійснює рухома система відліку по відношенню до нерухомої системи, називається переносним рухом. Рух, що здійснює ланка (точка) по відношенню до нерухомої (основної) системи відліку, називається абсолютним або складним. Нагадаємо теореми про додавання швидкостей та прискорень точки в її складному русі: абсолютна швидкість va точки дорівнює векторній сумі її переносної ve і відносної vr швидкостей, тобто Дана теорема ще носить назву паралелограма або трикутника швидкостей. Абсолютна швидкість знаходиться шляхом побудови паралелограма швидкостей. Вектори Абсолютне прискорення
Якщо переносний рух поступальний, то абсолютне прискорення точки дорівнює геометричній сумі двох прискорень: переносного та відносного. В свою чергу, при відносному обертальному русі прискорення
Методика побудови планів швидкостей та прискорень для двоповідкових груп полягає у складанні аналогічних векторних рівнянь для кожної ланки та спільному їх графічному розв’язку. Для прикладу розглянемо групу Ассура ІІ класу ІІ порядку першого виду (рис. 2.9). Швидкості точок А і С (якими група приєднується до механізму) відомі. Знайдемо швидкість точки В, яка є спільною для ланок 2 та 3. Для цього рух ланки 2 розкладаємо на переносний поступальний зі швидкістю
Інколи, для наочності, праві частини співвідношень (2.2) прирівнюють
Зазначимо, що такі векторні рівняння розв’язуються графічно, якщо вони містять не більше двох невідомих параметрів. Розглядувана група Ассура може бути приєднана лише до початкової ланки та стояка чи до раніше приєднаних (і відповідно розглянутих) груп Ассура, кінематичні параметри яких вже відомі. Отже, параметри переносного руху будуть визначеними. Вектори відносних швидкостей Відзначимо, що при аналізі векторних рівнянь часто прийнято підкреслювати вектор двома рисками, якщо він відомий як за величиною, так і за напрямком, і однією – якщо тільки за величиною або напрямком. Графічний розв’язок рівняння (2.3) наведено на рис. 2.9, б у вигляді плану швидкостей. Для його побудови вибираємо довільну точку
Рис. 2.9
Рівняння, які використовуються при побудові плану прискорень, відрізняються лише тим, що невідомі відносні прискорення точки в обертальному русі розкладають на складові
Виконаємо графічне додавання векторів згідно з рівняннями (2.4). З довільної точки Розглянемо друге рівняння. З полюса Розглянуті положення використовуються при побудові планів швидкостей і прискорень плоских механізмів. Розглянемо методику побудови планів швидкостей та прискорень механізмів ІІ класу. Приклад. Шестиланковий важільний механізм зі структурними групами Ассура ІІ класу першого та другого видів (рис. 2.10). Задано план механізму та закон руху початкової ланки ( Визначимо модуль лінійної швидкості т. А ланки О1 А, при обертанні її навколо т.О1, за формулою З довільно взятої точки рv полюса плану швидкостей відкладаємо відрізок рva, перпендикулярний до ланки Переходимо до побудови плану швидкостей першої групи Ассура. Швидкості точок А та Для визначення швидкості т.В, що одночасно належить ланкам 2 та 3, запишемо два векторні рівняння
Розв’язуємо цю систему рівнянь графічно. Згідно з першим рівнянням, через точку а плану швидкостей проводимо пряму, перпендикулярну до ланки АВ (до вектора швидкості
тобто, вимірявши відповідні відрізки на плані швидкостей в мм, множимо їх на масштаб Кутові швидкості ланок 2 та 3 визначаються рівностями
Визначимо швидкості інших точок, що належать до ланок даної групи. Аналогічно до точки В, розглянемо рух точки С по відношенню до точок В та
Швидкості точок В та Як випливає з виконаної побудови, трикутник В
Рис. 2.10
Відзначимо, що теорема подібності дійсна також при побудові планів прискорень. Вона дає можливість легко визначити швидкості будь-яких точок ланки, якщо відомі швидкості двох інших точок цієї ланки. Таким чином, швидкість точки С зручніше знаходити за теоремою подібності. Для цього на відрізку pvb, на плані швидкостей будуємо трикутник
з яких визначаємо довжини відрізків сpv та bc:
де Зробивши засічки з точки pv плану швидкостей радіусом pvc, а з точки b – радіусом bc, знайдемо точку с. Щоб не допустити помилки при визначенні положення точки с на плані швидкостей (засічку можна зробити по обидва боки від лінії pvb), потрібно користуватися правилом обходу: якщо обходити план швидкостей і ланку в одному напрямку, наприклад, за рухом стрілки годинника, починаючи відповідно з точок Швидкості центрів мас ланок знаходять, користуючись теоремою подібності. Наприклад, якщо задано, що центр мас другої ланки - точка
Переходимо до визначення швидкостей точок другої групи Ассура, яка складається з ланок 4 та 5. Знайдемо швидкість центра шарніра D, що з’єднує ланки 4 та 5 (
Відзначимо, що для таких структурних груп обмежуються першим рівнянням; повзун 5 рухається по нерухомій напрямній і абсолютна швидкість кожної його точки паралельна напрямній, vD//xx. При графічному розв’язку цих рівнянь достатньо через точку с плану швидкостей провести пряму, перпендикулярну до ланки CD на плані механізму, а через полюс pV – пряму, паралельну до напрямної хх. На перетині цих прямих і буде шукана точка d. Швидкість центра мас S4 знаходимо за теоремою подібності, в загальному випадку, із співвідношення
де З’єднавши з полюсом знайдену точки s4, отримуємо вектор, який зображає на плані швидкість даної точки. Підкреслимо, що, маючи план швидкостей механізму, можна визначити абсолютну та відносну швидкості будь-якої з точок механізму: вимірявши відповідний відрізок в мм на плані швидкостей, множимо його на масштаб плану
Кутову швидкість ланки 4 визначаємо за формулою Побудова плану прискорень. Послідовність побудови плану прискорень така ж, як для плану швидкостей. Повне прискорення точки А кривошипа 1 дорівнює геометричній сумі нормального та дотичного прискорень. У розглядуваному прикладі початкова ланка обертається рівномірно ( З точки pа відкладемо паралельно до кривошипа O1A (у напрямку від точки А до точки О1) відрізок довільної довжини paa. Тоді масштаб плану прискорень Розглянемо групу Ассура ІІ(2, 3). Для неї відомі прискорення точок А та О2. Визначимо прискорення центра шарніра В. Розглядаючи рух т.В по відношенню до т.А, а потім - до т.О2 , запишемо, відповідно, два векторні рівняння
Обчислимо величини нормальних складових Після цього можна векторні рівняння (2.5) розв’язувати графічно. Згідно з першим рівнянням, з точки a плану прискорень відкладаємо відрізок an2, що напрямлений паралельно до ланки AВ у напрямку від т.В до т.А. Через його кінець – т.n2 проводимо пряму, перпендикулярну до АВ (напрям Відрізок pab зображає, в масштабі Прискорення точок S2 та С знайдемо за теоремою подібності: точку s2 на плані прискорень розмістимо на середині відрізка ba (у даному прикладі центр мас S2 знаходиться посередині ланки АВ). Відрізок pas2 зображає прискорення т.S2; з пропорції Наступна структурна група утворена ланками 4 та 5. Повзун 5 рухається по нерухомій напрямній. Абсолютне прискорення кожної його точки паралельне цій напрямній. Така умова дозволяє записати одне рівняння для визначення прискорення точки D
Визначаємо нормальне прискорення
Виконаємо графічну побудову. З точки с плану прискорень паралельно до ланки CD в напрямку від т.D до т.С відкладемо відрізок cn4. Через точку n4 проводимо перпендикуляр до CD (напрям вектора
Визначимо кутові прискорення ланок
Для визначення напрямку кутового прискорення, наприклад, другої ланки Основні властивості плану швидкостей та прискорень. 1) Усі точки механізму, швидкості (прискорення) яких дорівнюють нулю, на плані швидкостей (прискорень) знаходяться в полюсі. 2) Усі вектори, що виходять з полюса плану швидкостей (прискорень), є векторами абсолютних швидкостей (прискорень). 3) Усі вектори плану, що з’єднують кінці векторів абсолютних швидкостей (прискорень), є векторами відносних швидкостей (прискорень). Замірявши відповідні відрізки (в мм) на плані швидкостей (прискорень) та помноживши їх на масштаб 4) Для плану швидкостей та прискорень дійсна теорема подібності. Приклад 2. На рис. 2.11, а показана кінематична схема механізму поперечно-стругального верстата. До його складу входять початкова ланка 1 та дві групи Ассура ІІ класу: група, що складається з ланок 2 та 3 третього виду, та група ІІ(4,5) п’ятого виду. Необхідно побудувати плани швидкостей і прискорень для положення визначеного кутом Знаходимо швидкість т.В, яка належить ланці 1, Від полюса
Рис. 2.11 Переходимо до визначення швидкостей точок ланок першої структурної групи. Відомі швидкості точок В і С, які належать зовнішнім кінематичним парам групи: швидкість т.
За першим рівнянням з точки b, кінця вектора Використовуючи теорему подібності, знаходимо положення точки D на плані швидкостей
Відкладаємо відрізок сd на продовженні відрізка cb3 Швидкість т.D5 , яка належить ланці 5, визначаємо з рівняння
Усі точки ланки 5 рухаються вздовж напрямної EF, тобто абсолютна швидкість т.D5 паралельна напрямній, Положення т.S3 знаходимо за теоремою подібності з пропорції
Вимірявши відповідні відрізки в мм, множимо їх на масштаб
Кутову швидкість ланки 3 визначимо за формулою Побудова плану прискорень. Прискорення т.В, яка належить ланці 1 кривошипу, визначається за формулою
Від полюса pa (рис. 2.11, г) відкладаємо відрізок pab паралельно до ланки АВ (у напрямку від т.В до т.А), який зображує прискорення Визначаємо прискорення т.
У першому рівнянні
Щоб знайти напрямок вектора
Відкладаємо від точки b плану прискорень відрізок bk, а від полюса pa відрізок pan3. З точки k проводимо лінію, паралельну до ВС, а з точки n3 - лінію, перпендикулярну ВС до їх перетину між собою. Точку перетину b3 з’єднуємо з полюсом і одержуємо відрізок pab3, який зображує прискорення
Щоб знайти прискорення точки
Прискорення
Модуль кутового прискорення
Напрямок |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 432. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 .
. , для якої потрібно знайти похідну, задана таблично. При розробці програм для чисельного диференціювання на ЕОМ використовують інтерполяційні формули Ньютона, Стірлінга, Бесселя та ін..
, для якої потрібно знайти похідну, задана таблично. При розробці програм для чисельного диференціювання на ЕОМ використовують інтерполяційні формули Ньютона, Стірлінга, Бесселя та ін.. її значень у n рівновіддалених точках
її значень у n рівновіддалених точках  з кроком
з кроком  . Шукане значення похідної
. Шукане значення похідної  обчислюється за формулами
обчислюється за формулами ,
, ,
, .
. , що задана множиною значень аргументу
, що задана множиною значень аргументу  , виконують за формулами трапеції, Сімпсона та інших. Наведемо, для прикладу, формулу трапеції. У рівновіддалених значеннях аргументу
, виконують за формулами трапеції, Сімпсона та інших. Наведемо, для прикладу, формулу трапеції. У рівновіддалених значеннях аргументу  обчислюють за формулою
обчислюють за формулою (
( 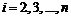 ).
). точки А перпендикулярна до кривошипа ОА (напрямлена по дотичній до траєкторії т.А) і спрямована у бік його обертання. Зобразимо швидкість точки А деяким вектором, відкладеним з довільної точки рv, яку приймаємо за полюс плану швидкостей (рис. 2.8, б). Цей вектор перпендикулярний до прямої ОА і напрямлений в бік обертання кривошипа. В кінці вектора поставимо точку а. Довжина відрізка рvа може бути прийнята довільною. Переважно вона вибирається при визначенні масштабу
точки А перпендикулярна до кривошипа ОА (напрямлена по дотичній до траєкторії т.А) і спрямована у бік його обертання. Зобразимо швидкість точки А деяким вектором, відкладеним з довільної точки рv, яку приймаємо за полюс плану швидкостей (рис. 2.8, б). Цей вектор перпендикулярний до прямої ОА і напрямлений в бік обертання кривошипа. В кінці вектора поставимо точку а. Довжина відрізка рvа може бути прийнята довільною. Переважно вона вибирається при визначенні масштабу  ,
,  , з урахуванням рекомендацій з вибору масштабів; модуль швидкості т.А визначається за формулою vA=ωlOA, м/с, для визначення кутової швидкості користуються формулою
, з урахуванням рекомендацій з вибору масштабів; модуль швидкості т.А визначається за формулою vA=ωlOA, м/с, для визначення кутової швидкості користуються формулою 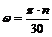 ,
,  ; де п – частота обертання. Аналогічні міркування проводять, при потребі, відносно будь-якої іншої точки кривошипа. Звичайно, швидкості та прискорення точок, що належать осі обертання, дорівнюють нулю і, відповідно, на планах вони знаходяться в полюсі (т.О, S ). Отже, вектор
; де п – частота обертання. Аналогічні міркування проводять, при потребі, відносно будь-якої іншої точки кривошипа. Звичайно, швидкості та прискорення точок, що належать осі обертання, дорівнюють нулю і, відповідно, на планах вони знаходяться в полюсі (т.О, S ). Отже, вектор  представляє собою план швидкостей початкової ланки для положен
представляє собою план швидкостей початкової ланки для положен  ня, що визначається кутовою координатою
ня, що визначається кутовою координатою 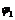 .
. ;
; ;
; .
. ,
,  , попередньо задавшись довжиною відрізка
, попередньо задавшись довжиною відрізка  , що зображує
, що зображує  нормальне прискорення на плані. Прийнявши довільну точку
нормальне прискорення на плані. Прийнявши довільну точку  за полюс плану прискорень, відкладемо вектор
за полюс плану прискорень, відкладемо вектор  – довжину відрізка , що зображає
– довжину відрізка , що зображає  дотичне прискорення на плані прискорень.
дотичне прискорення на плані прискорень. ,
, 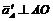 . Відкладаємо з точки
. Відкладаємо з точки  плану відрізок
плану відрізок 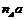 і отримуємо вектор
і отримуємо вектор  повного прискорення точки А.
повного прискорення точки А. ), тобто
), тобто  , а отже
, а отже  , і
, і  . У цьому випадку план прискорень має вигляд, зображений на рис. 2.8, г.
. У цьому випадку план прискорень має вигляд, зображений на рис. 2.8, г. .
. ,
, 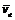 ,
,  швидкостей мають напрямки по дотичній до відповідної траєкторії.
швидкостей мають напрямки по дотичній до відповідної траєкторії. довільної точки ланки дорівнює векторній сумі переносного
довільної точки ланки дорівнює векторній сумі переносного 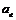 , відносного
, відносного 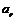 і коріолісового
і коріолісового  прискорень, тобто
прискорень, тобто .
. .
. . Для ланки 3 аналогічно – на переносний поступальний зі швидкістю
. Для ланки 3 аналогічно – на переносний поступальний зі швидкістю  т.С і відносний обертальний - навколо точки С зі швидкістю
т.С і відносний обертальний - навколо точки С зі швидкістю  . Скориставшись теоремою про додавання швидкостей точки в її складному русі, запишемо векторні рівняння, що зв’язують швидкості точок В , А та С
. Скориставшись теоремою про додавання швидкостей точки в її складному русі, запишемо векторні рівняння, що зв’язують швидкості точок В , А та С , (2.2)
, (2.2) .
.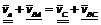 . (2.3)
. (2.3)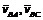 в обертальному русі відомі лише за напрямком - перпендикулярні до відповідної ланки (по дотичній до траєкторії руху).
в обертальному русі відомі лише за напрямком - перпендикулярні до відповідної ланки (по дотичній до траєкторії руху). - полюс плану швидкостей. Від неї відкладаємо вектор відомої швидкості
- полюс плану швидкостей. Від неї відкладаємо вектор відомої швидкості 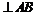 ). Такі ж міркування можна навести при розгляді правої частини рівняння (2.3). У розглядуваному прикладі точка С ланки 3 приєднана до стояка,
). Такі ж міркування можна навести при розгляді правої частини рівняння (2.3). У розглядуваному прикладі точка С ланки 3 приєднана до стояка,  . Отже, на плані швидкостей т.С знаходиться у полюсі. До вектора швидкості
. Отже, на плані швидкостей т.С знаходиться у полюсі. До вектора швидкості  лінію, яка показує напрямок вектора відносної швидкості – перпендикуляр до ланки ВС (
лінію, яка показує напрямок вектора відносної швидкості – перпендикуляр до ланки ВС (  ). Точка перетину в цих ліній визначить величину та напрямок швидкості точки В.
). Точка перетину в цих ліній визначить величину та напрямок швидкості точки В.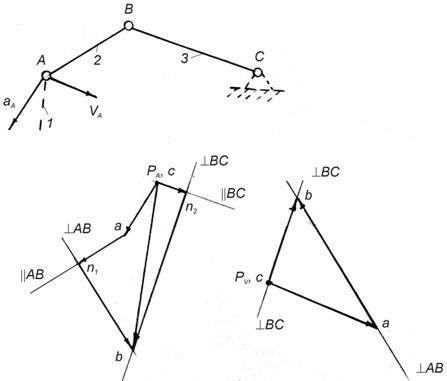
 , (2.4)
, (2.4) .
.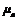 вектор відомого прискорення т.А. З кінця цього вектора, точка а, відкладемо вектор
вектор відомого прискорення т.А. З кінця цього вектора, точка а, відкладемо вектор  нормального прискорення точки В навколо т.А. Нормальне прискорення напрямлене по лінії АВ до центра обертання - точки А. Модуль його порахований після побудови плану швидкостей за формулою
нормального прискорення точки В навколо т.А. Нормальне прискорення напрямлене по лінії АВ до центра обертання - точки А. Модуль його порахований після побудови плану швидкостей за формулою  . Довжина відрізка, який зображає
. Довжина відрізка, який зображає  . Через його кінець (точку
. Через його кінець (точку  ) проводимо лінію дотичного прискорення
) проводимо лінію дотичного прискорення  , направленого перпендикулярно до АВ.
, направленого перпендикулярно до АВ. ) відкладемо вектор, який зображає
) відкладемо вектор, який зображає  , нормальне прискорення, у вигляді відрізка
, нормальне прискорення, у вигляді відрізка  (
(  , має напрям від точки В до С). Через його кінець (точку
, має напрям від точки В до С). Через його кінець (точку  ) проведемо лінію-напрямок дотичного прискорення
) проведемо лінію-напрямок дотичного прискорення  до перетину з лінією напрямком прискорення
до перетину з лінією напрямком прискорення 
 .
. і напрямлений в бік руху кривошипа. Швидкість т.А на плані швидкостей показано відрізком рva, тобто масштаб плану швидкостей
і напрямлений в бік руху кривошипа. Швидкість т.А на плані швидкостей показано відрізком рva, тобто масштаб плану швидкостей  .
.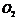 , що належать до зовнішніх кінематичних пар цієї групи, відомі (
, що належать до зовнішніх кінематичних пар цієї групи, відомі (  ;
; 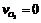 ).
). ,
, .
. додаємо вектор швидкості
додаємо вектор швидкості  ). Згідно з другим рівнянням, через полюс рv проводимо пряму, перпендикулярну до ланки
). Згідно з другим рівнянням, через полюс рv проводимо пряму, перпендикулярну до ланки  (до швидкості т.
(до швидкості т.  ). Точка перетину b цих перпендикулярів є кінцем вектора pvb, що зображує на плані у масштабі
). Точка перетину b цих перпендикулярів є кінцем вектора pvb, що зображує на плані у масштабі  абсолютну швидкість т.В. Величини невідомих швидкостей визначають за формулами
абсолютну швидкість т.В. Величини невідомих швидкостей визначають за формулами ,
, 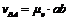 ,
, ,
,  .
. ,
,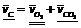 .
. і
і  , як швидкості в обертальному русі, перпендикулярні, відповідно, до ланок ВС та С
, як швидкості в обертальному русі, перпендикулярні, відповідно, до ланок ВС та С  .
. ,
, 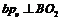 ,
,  ). При цьому, трикутники
). При цьому, трикутники  та
та  повернуті, один відносно одного, на прямий кут в напрямку миттєвого обертання. Цю властивість подібності фігури відносних швидкостей на плані швидкостей (прискорень), до фігури ланки на схемі механізму, називають теоремою подібності: план відносних швидкостей (прискорень) точок однієї і тієї ж ланки, подібний до відповідної фігури на схемі механізму.
повернуті, один відносно одного, на прямий кут в напрямку миттєвого обертання. Цю властивість подібності фігури відносних швидкостей на плані швидкостей (прискорень), до фігури ланки на схемі механізму, називають теоремою подібності: план відносних швидкостей (прискорень) точок однієї і тієї ж ланки, подібний до відповідної фігури на схемі механізму.
 , подібний до трикутника
, подібний до трикутника  , або
, або  ,
,
 ,
, – дійсні розміри ланок,
– дійсні розміри ланок, 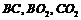 – розміри ланок на схемі механізму;
– розміри ланок на схемі механізму;  – відповідні відрізки на плані швидкостей.
– відповідні відрізки на плані швидкостей. та
та  . Зазначимо, що теорема подібності справедлива лише для незмінної системи твердого тіла, тобто однієї ланки. Одночасно для декількох ланок, групи Ассура чи механізму в цілому вона не дійсна.
. Зазначимо, що теорема подібності справедлива лише для незмінної системи твердого тіла, тобто однієї ланки. Одночасно для декількох ланок, групи Ассура чи механізму в цілому вона не дійсна. лежить на середині ланки АВ, то на плані швидкостей т.
лежить на середині ланки АВ, то на плані швидкостей т. 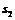 з полюсом, знаходимо вектор швидкості
з полюсом, знаходимо вектор швидкості  центра мас шатуна 2. Модуль вектора швидкості визначається за формулою
центра мас шатуна 2. Модуль вектора швидкості визначається за формулою .
. ). Розглядаючи рух т.D по відношенню до т.C, а потім – до т.D0 (точки, що належить напрямній хх, і в даному положенні механізму співпадає з точкою D на повзуні), запишемо два векторні рівняння
). Розглядаючи рух т.D по відношенню до т.C, а потім – до т.D0 (точки, що належить напрямній хх, і в даному положенні механізму співпадає з точкою D на повзуні), запишемо два векторні рівняння ,
, .
. , або
, або  , звідки
, звідки  ,
, ,
,  – дійсні розміри ланок,
– дійсні розміри ланок,  ,
,  – розміри ланок на схемі механізму;
– розміри ланок на схемі механізму;  ,
,  – відповідні відрізки на плані швидкостей.
– відповідні відрізки на плані швидкостей. ,
,  ,
,  .
. . Напрямки кутових швидкостей ланок знаходимо за допомогою умовного переносу векторів відносних швидкостей на схему механізму. Наприклад, для ланки 4 швидкість
. Напрямки кутових швидкостей ланок знаходимо за допомогою умовного переносу векторів відносних швидкостей на схему механізму. Наприклад, для ланки 4 швидкість  , яка на плані швидкостей зображена вектором
, яка на плані швидкостей зображена вектором 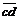 , умовно переносимо в точку D на схемі механізму. Вектор
, умовно переносимо в точку D на схемі механізму. Вектор  також напрямлена проти руху стрілки годинника.
також напрямлена проти руху стрілки годинника. або
або 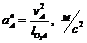 .
. .
.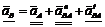 ,
,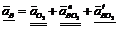 . (2.5)
. (2.5)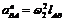 ,
,  та довжини відрізків, які будуть зображати їх на плані,
та довжини відрізків, які будуть зображати їх на плані, 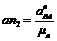 ,
, 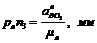 .
. ). Згідно з другим рівнянням, з полюса pa паралельно до ВО2, у напрямку від т.В до т.О2, відкладаємо відрізок pan3.. Через т.n3 проводимо перпендикуляр до ВО2 (напрям
). Згідно з другим рівнянням, з полюса pa паралельно до ВО2, у напрямку від т.В до т.О2, відкладаємо відрізок pan3.. Через т.n3 проводимо перпендикуляр до ВО2 (напрям  ). На перетині дотичних складових (перпендикулярів) отримаємо шукану точку b.
). На перетині дотичних складових (перпендикулярів) отримаємо шукану точку b.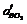 , а відрізок ab - повне відносне прискорення
, а відрізок ab - повне відносне прискорення  т.В відносно т.А.
т.В відносно т.А. вираховуємо довжини відрізків bc та cpa та методом засічок знаходимо точку с на плані прискорень. При цьому має бути збережена схожість фігур ВСО2 на схемі механізму та bcpa на плані прискорень.
вираховуємо довжини відрізків bc та cpa та методом засічок знаходимо точку с на плані прискорень. При цьому має бути збережена схожість фігур ВСО2 на схемі механізму та bcpa на плані прискорень. .
. та відрізок, що буде зображати його на плані прискорень,
та відрізок, що буде зображати його на плані прискорень, .
. ). Через полюс pa проводимо пряму, паралельну до напрямної (напрям вектора абсолютного прискорення
). Через полюс pa проводимо пряму, паралельну до напрямної (напрям вектора абсолютного прискорення  ). Ці лінії перетнуться в шуканій точці d. Згідно співвідношення
). Ці лінії перетнуться в шуканій точці d. Згідно співвідношення 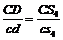 на відрізку dc розмістимо точку s4. План прискорень побудований. Величини прискорень точок механізму дорівнюють добутку довжини відповідного відрізка з плану прискорень на масштаб плану. Наприклад:
на відрізку dc розмістимо точку s4. План прискорень побудований. Величини прискорень точок механізму дорівнюють добутку довжини відповідного відрізка з плану прискорень на масштаб плану. Наприклад: ,
,  .
.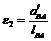 ,
,  ,
,  .
. , уявно переносимо вектор дотичного прискорення
, уявно переносимо вектор дотичного прискорення  , знаходимо дійсні (за модулем) значення швидкостей (прискорень).
, знаходимо дійсні (за модулем) значення швидкостей (прискорень).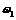 =const.
=const. м/с.
м/с. , який зображує вектор швидкості vB (Рис. 2.11, б). При цьому масштаб плану швидкостей дорівнює
, який зображує вектор швидкості vB (Рис. 2.11, б). При цьому масштаб плану швидкостей дорівнює

 , яка належить ланці 2 (повзуну), дорівнює швидкості т. В кривошипа (першої ланки), тобто
, яка належить ланці 2 (повзуну), дорівнює швидкості т. В кривошипа (першої ланки), тобто 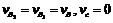 . Невідома швидкість точки
. Невідома швидкість точки 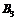 , яка належить ланці 3, кулісi і в даному положенні механізму, співпадає з т. В, що лежить на кривошипі (повзуні). Для її визначення записуємо систему векторних рівнянь
, яка належить ланці 3, кулісi і в даному положенні механізму, співпадає з т. В, що лежить на кривошипі (повзуні). Для її визначення записуємо систему векторних рівнянь
 (швидкості т.В) проводимо пряму, паралельну до ланки CD (
(швидкості т.В) проводимо пряму, паралельну до ланки CD (  є швидкість відносного поступального руху повзуна 2 по напрямній 3; напрямлена вздовж неї). За другим рівнянням з точки с , яка співпадає з полюсом pV, (vc = 0), проводимо пряму, перпендикулярну до ВС. На перетині цих прямих одержуємо точку b3. Вектор
є швидкість відносного поступального руху повзуна 2 по напрямній 3; напрямлена вздовж неї). За другим рівнянням з точки с , яка співпадає з полюсом pV, (vc = 0), проводимо пряму, перпендикулярну до ВС. На перетині цих прямих одержуємо точку b3. Вектор  зображує швидкість
зображує швидкість  точки
точки 
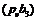 , знаходимо точку d.
, знаходимо точку d.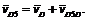
 Таким чином, з полюса pv проводимо пряму, паралельну до EF, а з точки d – пряму, паралельну до КМ. На перетині одержуємо точку d5 . Сполучаємо її з полюсом pV.
Таким чином, з полюса pv проводимо пряму, паралельну до EF, а з точки d – пряму, паралельну до КМ. На перетині одержуємо точку d5 . Сполучаємо її з полюсом pV. .
. .
. . Напрямок цієї швидкості знаходимо за допомогою вектора швидкості
. Напрямок цієї швидкості знаходимо за допомогою вектора швидкості  напрямлена у той же бік.
напрямлена у той же бік.
 (
( 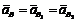 ). Масштаб плану прискорень при цьому
). Масштаб плану прискорень при цьому  .
.
 , - коріолісове прискорення, яке з’явилось у результаті складання відносного поступального руху повзуна 2 по напрямній 3 зі швидкістю
, - коріолісове прискорення, яке з’явилось у результаті складання відносного поступального руху повзуна 2 по напрямній 3 зі швидкістю  та переносного обертального руху цієї напрямної зі швидкістю
та переносного обертального руху цієї напрямної зі швидкістю  .
.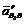 є прискоренням відносного поступального руху повзуна 2 по напрямній 3 і напрямлене вздовж ланки CD. Величина (модуль) його невідома. Нормальне прискорення
є прискоренням відносного поступального руху повзуна 2 по напрямній 3 і напрямлене вздовж ланки CD. Величина (модуль) його невідома. Нормальне прискорення  визначається за формулою
визначається за формулою 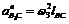 , воно напрямлене від точки В до точки С паралельно до ланки СВ. Дотичне прискорення
, воно напрямлене від точки В до точки С паралельно до ланки СВ. Дотичне прискорення 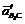 напрямлене перпендикулярно до ланки ВС. Визначаємо відрізки bk i pan3 , які зображують прискорення
напрямлене перпендикулярно до ланки ВС. Визначаємо відрізки bk i pan3 , які зображують прискорення  на плані
на плані
 .
. точки
точки  звідки
звідки  .
. , яка належить ланці 5, записуємо векторне рівняння
, яка належить ланці 5, записуємо векторне рівняння ,
,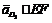 .
.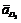 напрямлене вздовж напрямної EF, а відносне (релятивне) прискорення
напрямлене вздовж напрямної EF, а відносне (релятивне) прискорення 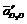 - вздовж КМ. З полюса рa проводимо лінію, паралельну до EF , а з точки d – лінію, паралельну до КМ. На перетині цих ліній одержуємо точку
- вздовж КМ. З полюса рa проводимо лінію, паралельну до EF , а з точки d – лінію, паралельну до КМ. На перетині цих ліній одержуємо точку  . Величини знайдених прискорень дорівнюють
. Величини знайдених прискорень дорівнюють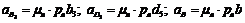 ;
; .
.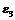 ланки 3 знайдемо за формулою
ланки 3 знайдемо за формулою .
. , що зображає
, що зображає