
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ВИЗНАЧЕННЯ МОМЕНТУ ІНЕРЦІЇ СИСТЕМИСтр 1 из 3Следующая ⇒ Лабораторна робота № 1 ВИВЧЕННЯ КРИВОЛІНІЙНОГО РУХУ
Мета роботи – визначити деякі кінематичні характеристики (горизонтальну і вертикальну складові швидкості, повну швидкість, нормальну і тангенціальну (дотичну) складові повного прискорення, а також радіус кривизни траєкторії) руху тіла, що кинуте горизонтально в полі тяжіння Землі, в заданій точці траєкторії. Прилади і обладнання: криволінійний жолоб, стальна кулька, обмежувальний ящик, масштабна лінійка, звичайний та копіювальний папір. Теоретичні відомості Якщо матеріальна точка рухається за криволінійною траєкторією, то вектор її лінійної швидкості збігається з дотичною до траєкторії. При цьому вектор швидкості може змінюватись в загальному випадку як за модулем, так і за напрямком. Вектор тангенціального прискорення
Напрямок вектора тангенціального прискорення в кожній точці траєкторії (див. рис.1, точка M) збігається з напрямком вектора повної швидкості, а його модуль визначається першою похідною від швидкості за часом: Вектор нормального прискорення спрямований до центра кривизни траєкторії під кутом 900 до вектора повної швидкості. Його модуль  При кидані деякого тіла в горизонтальному напрямку (вздовж осі ОХ) його рух обумовлюється рухом за інерцією в горизонтальному напрямку і рухом під дією сили тяжіння – в вертикальному. Згідно принципу незалежного складання рухів ці два рухи дають результуючий рух за криволінійною траєкторією. Його описує рівняння руху в двох координатах: ОХ: ОУ: де vВ = vy: Рівняння (1) - (3) дозволяють з відомих початкових умов визначити кінематичні характеристики руху матеріальної точки в будь-який момент часу (це є пряма задача кінематики), наприклад, для моменту падіння маємо:
В даній лабораторній роботі відомими з експерименту є величини H i L, що дозволяє розрахувати інші відповідні кінематичні характеристики.
Опис методу Для створення горизонтального руху тіла (стальної кульки) застосовується жолоб N, що закріплений на тримачі D (рис.2). Кульку утримують над жолобом на рівні його верхнього краю, а потім відпускають. Нижній кінець жолоба спрямований горизонтально, тому і вектор швидкості кульки в точці вильоту спрямований горизонтально.
Значення горизонтальної складової швидкості є однаковим в кожній точці траєкторії і дорівнює значення вертикальної складової дорівнює
Для величини повної швидкості в точці падіння, враховуючи вищенаведені формули, маємо
Повне прискорення в будь-якій точці дорівнює прискоренню вільного падіння Знайдемо формули для обчислення цих величин. З рис.3 бачимо, що трикутники ABC і DFC є подібні, тому маємо Також Знаючи
В роботі необхідно визначитивеличини: vГ, vВ, v, at, an, a, R в точці падіння, виходячи з виміряних значень L і H.
Порядок виконання роботи Виміри 1. Закріпити жолоб N на тримачі D так, щоб було зручно виконувати експериментальну частину роботи (дивись рис.2). 2. Розташувати біля жолоба обмежувальний ящик так, щоб його відкритий бік був звернений до жолоба і розташовувався на одній вертикалі з його нижнім обрізом. Зробити пробні кидки кульки. Якщо кулька не долітає до середини ящика, чи, навпаки, перелітає ящик, то відрегулюйте висоту кріплення жолоба на тримачі. 3. В обмежувальний ящик покласти аркуш копіювального паперу чутливим боком догори і накрити аркушем чистого паперу. Край аркушу сумістити з краєм відкритого боку обмежувального ящика. 4. Зробити 10 кидків кульки, прагнучи робити це однаковим чином і фіксуючи рукою положення паперу відносно жолобу. 5. Перегорнути аркуш паперу і виміряти лінійкою відстані від краю паперу до точок, де падала кулька. Занести результати вимірів в табл.1. 6. Зробити одноразовий вимір висоти H вздовж вертикалі від нижнього краю жолоба до площини, на яку падає кулька. Обчислення середніх значень Обчислити середні значення L, vГ, vВ, v, at, an, a, R. Результат для <L> записати внизу табл.1. В цій таблиці також записати величину прийнятої довірчої імовірності і значення коефіцієнтів Стьюдента (див. Додаток 1).
Обчислення похибок прямих вимірювань Похибка вимірювання L має три складові: випадкова похибка (
Тоді загальна похибка вимірювання L:
= Таблиця 1. Результати вимірів і вихідні дані для розрахунку похибок вимірювання
H = ..... , прийнята довірча імовірність a = ..... , коефіцієнт Стьюдента ta,¥= ..... , коефіцієнт Стьюдента ta,10= .....
Таблиця 2 Характеристики мір, необхідні для розрахунку похибок вимірювання
Похибка вимірювання H має дві складові: інструментальна похибка (DHін) і похибка відліку(DHвід). Записати результати прямих вимірювань в стандартній формі (див. Додаток 3): L = .....m ....., EL = ....% H = .....m ....., EH = ....% , для a = 0,95. Тут також записуємо значення використаної сталої
Обчислення похибок непрямих вимірювань За вказівкою викладача обчислити похибки непрямих вимірювань для величин vГ, vВ, v .Для цього: 1. Виводимо формули для розрахунку відносних похибок вимірювання vГ (vВ, v ). Наприклад, для vГ : а)записуємо функціональну залежність величини б) логарифмуємо цей вираз в) знаходимо часткові похідні г) записуємо формулу для відносної похибки 2. Оскільки Аналогічно виконуємо розрахунки для vВ таv .
Представлення результатів вимірювання. Прямі вимірювання: L = ..... ±..... , EL = ....% , для a = 0,95. H = ..... ±..... , EH = ....% , для a = 0,95.
Непрямі вимірювання: vГ =..... m ..... , Ev = ....% , для a = 0,95. (vВ =.....m ..... ,Ev = ....% , для a ==0,95), (v = .....m ..... , Ev = ....% , для a = 0,95). at = ..... , an = ..... , a = ..... , R = .....
Лабораторна робота № 2
ВИЗНАЧЕННЯ МОМЕНТУ ІНЕРЦІЇ СИСТЕМИ |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 239. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 визначається швидкістю зміни вектора швидкості
визначається швидкістю зміни вектора швидкості 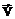 за модулем, вектор нормального (доцентрового) прискорення
за модулем, вектор нормального (доцентрового) прискорення 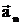 - швидкістю зміни вектора швидкості за напрямком.
- швидкістю зміни вектора швидкості за напрямком.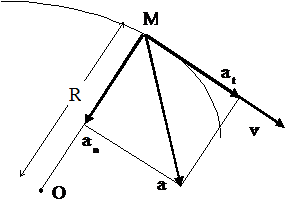
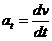 .
.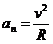 , де v – повна швидкість в точці траєкторії M, R – радіус кривизни траєкторії в цій точці. Вектори тангенціального і нормального прискорення є взаємно перпендикулярними складовими повного прискорення
, де v – повна швидкість в точці траєкторії M, R – радіус кривизни траєкторії в цій точці. Вектори тангенціального і нормального прискорення є взаємно перпендикулярними складовими повного прискорення  , яке дорівнює їх векторній (геометричній) сумі:
, яке дорівнює їх векторній (геометричній) сумі:  . Модуль вектора повного прискорення
. Модуль вектора повного прискорення  .
. , (1)
, (1) , (2)
, (2) - початкова швидкість вздовж осі ОХ (початкова швидкість в вертикальному напрямку дорівнює нулю), H – висота, з якій падає кулька, g – прискорення вільного падіння. Ми нехтуємо силою опору повітря і тому вважаємо рух вздовж осі ОХ рівномірним, тобто горизонтальна складова швидкості завжди vг = vox = vо. Цей рух і рух по вертикалі синхронізовані у часі, але є незалежними. Диференціювання по часу другого рівняння дає вираз для величини вертикальної складової швидкості
- початкова швидкість вздовж осі ОХ (початкова швидкість в вертикальному напрямку дорівнює нулю), H – висота, з якій падає кулька, g – прискорення вільного падіння. Ми нехтуємо силою опору повітря і тому вважаємо рух вздовж осі ОХ рівномірним, тобто горизонтальна складова швидкості завжди vг = vox = vо. Цей рух і рух по вертикалі синхронізовані у часі, але є незалежними. Диференціювання по часу другого рівняння дає вираз для величини вертикальної складової швидкості 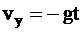 . (3)
. (3)
 ;
;  ;
;  (4)
(4) (5)
(5) . (6)
. (6) . (7)
. (7)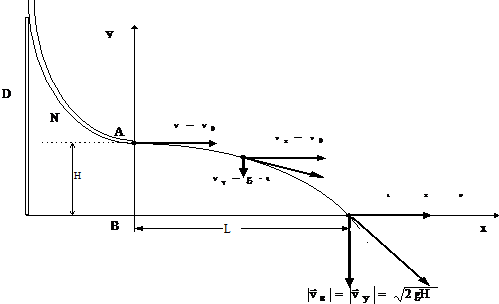
 . Розкладемо його на дві складові – тангенціальну (дотичну)
. Розкладемо його на дві складові – тангенціальну (дотичну)  і нормальну (доцентрову)
і нормальну (доцентрову)  , звідки
, звідки  . (8)
. (8) , звідки
, звідки  . (9)
. (9) і
і  для точки С, можна визначити радіус кривизни траєкторії в цій точці:
для точки С, можна визначити радіус кривизни траєкторії в цій точці:  (10)
(10)
 ), інструментальна похибка (DLін) і похибка відліку (DLвід):
), інструментальна похибка (DLін) і похибка відліку (DLвід): =
= 
 ,
,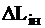 =
=  ,
, =
=  .
. =
=
 = .....
= .....
 .
. .
. ,
,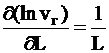 та
та  , похибкою заокруглення сталої g нехтуємо,
, похибкою заокруглення сталої g нехтуємо, .
. , то шукана похибка вимірювання
, то шукана похибка вимірювання 