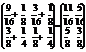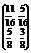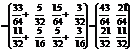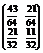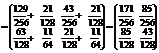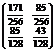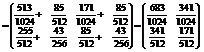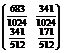Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Знайти об’єм піраміди ABCD,якщо А(1,3,-2), В(3,-2,1), С(1,0,-4), D(1,0,-3) ⇐ ПредыдущаяСтр 2 из 2 Дано: А(1,3,-2), В(3,-2,1), С(1,0,-4), D(1,0,-3) Знайти: V-? Розв’язання: Розглянемо три вектора
Отримаємо:
Об’єм піраміди знаходимо по формулі:
Підставимо значення:
Оскільки об’єм піраміди є додатне число, то маємо V=1 (од3.)
24.Пасажири, що стають в чергу за квитками в залізничну касу, утворюють найпростіший потік, в якому інтервал часу між моментами прибуття пасажирів є випадкова величина Х з показниковим законом розподілу:
Знайти числові характеристики Розв’язання: Скористуємося формулою: Враховуя,що f(t)=0 при t<0 і f(t)= М(Х)= Інтегруючи по частинах по формулі: Положив u=t,dv= М(Х)= Знайдемо дисперсію. Скористуємося формулою:
Інтегруючи двічі по частинах знайдемо
Відповідь: М(Х)=2;D(X)=4
25.Знайти розв’язок задачі Коші Розв’язання: Складемо характеристичне рівняння k2-3k+2=0 і знайдемо його корені k2-3k+2=0 Д=9-8=1 Х1= Х2= Загальний розв’язок рівняння має вигляд у=С1е2х+С2ех. Скористаємось початковими умовами. Оскільки у’=2С1+С2,то
Звідки С1=1; С2=-1 Знаходимо шуканий розв’язок: у= е2х- ех Відповідь:у= е2х-ех
Знайти числові характеристики випадкової величини Х,яка рівномірно розподілена в інтервалі (3,9) Розв’язання: Рівномірним називають розподіл ймовірностей непереривної величини х,якщо на інтервалі (а,б),котрому належать всі значення х, щільність зберігає постійне значення f(х)=1/(а+б).  Числовими характеристиками випадкової величини є математичне сподівання,дисперсія і середне квадратичне відхилення випадкової величини. Знайдемо математичне сподівання випадкової величини:
М(х)=(3+9)2=6 Знайдемо дисперсію випадкової змінної використовуючи формулу: Д(х)=М(х2)-М2(х) М(х2)=
Д(х)= Д(х)=(9-3)2/12=3 Середне квадратичне відхилення випадкової величини дорівнює квадратичному кореню з дисперсії
Відповідь: М(х)=6; Д(х)=3;σ(х)=1,73
27.Знайти площу фігури, яка обмежена лініями Розв’язання: По формулі S=
O(0,0)
28.Дано точки А(-1;5;0),В(2;α;4),С(1;0;-4).При якому значенні α вектори АВ Розв’язання: Із правила скалярного добутку векторів Знайдемо вектори
По правилу скалярного добутку знайдемо: 6-5(α-5)-16=0 6-5α+25-16=0 -5α=-15 α =3 Перевіряємо:
Відповідь: α =3 Дано точки А(-1;5),В(2;4),С(0;-4).Записати рівняння прямої, яка проходить через точку А перпендикулярно ВС. Розв’язання: Рівняння площини, яка проходить через точку Мо(хо;уо;zo) перпендикулярно до вектора Знайдемо вектор
Тоді, виходячи з формули, знаходимо шукане рівняння: -2(х+1)-8(у-5)=0 -2х-8х+38=0 Відповідь: -2х-8х+38=0
Знайти фінальний розподіл Ймовірностей станів Марковського ланцюга з дискретним часом, граф Якого має вигляд
Розв’язання: Р12= Р12=
Р13=
Р14=
Р15=
Таким чином, фінальний розподіл ймовірностей станів Марковського ланцюга з дискретним часом дорівнює Відповідь:
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 293. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
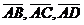 на котрих побудована піраміда зная координати початку і кінця кожного вектора, знайдемо проекції цих векторів на осі прямокутної системи координат:
на котрих побудована піраміда зная координати початку і кінця кожного вектора, знайдемо проекції цих векторів на осі прямокутної системи координат: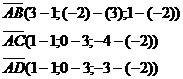
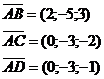
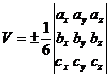
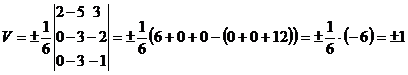
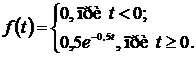

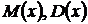 .
.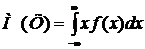 .
.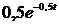 при
при 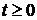 ,отримаємо
,отримаємо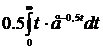
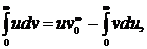
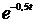 dt,звідси du=dt, v=1/0,5*
dt,звідси du=dt, v=1/0,5* 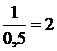
 .Враховуя,що f(t)=0 при t<0, М(Х)=
.Враховуя,що f(t)=0 при t<0, М(Х)= 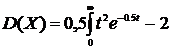 .
.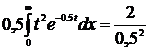 . Отже, шукана дисперсія D(X)=
. Отже, шукана дисперсія D(X)= 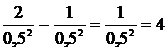
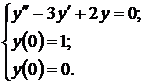
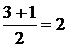
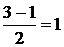 Х1=2;Х2=1
Х1=2;Х2=1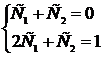 ;
;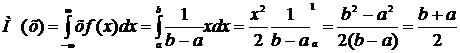
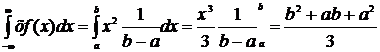
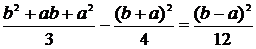
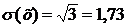
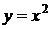 ,
, 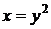 .
.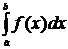 маємо S=
маємо S= 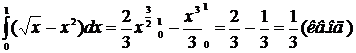
 y
y

 y=x2 x=y2
y=x2 x=y2


 A(1,1)
A(1,1)
 x
x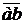 =
= 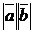 cosφ,слідує, що якщо вектори перпендикулярні, то їх скалярний добуток дорівнює нулю.
cosφ,слідує, що якщо вектори перпендикулярні, то їх скалярний добуток дорівнює нулю.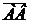 та
та 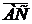 .Щоб знайти координати вектора заданими координатами початку і кінця, треба у координат кінця відняти координати початку.
.Щоб знайти координати вектора заданими координатами початку і кінця, треба у координат кінця відняти координати початку.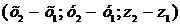
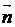 =(А;В;С) є А(х-хо)+В(у-уо)+С(z- zo)=0
=(А;В;С) є А(х-хо)+В(у-уо)+С(z- zo)=0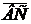 . Щоб знайти координати вектора заданими координатами початку і кінця, треба у координат кінця відняти координати початку.
. Щоб знайти координати вектора заданими координатами початку і кінця, треба у координат кінця відняти координати початку.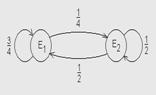
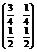
 *
*  =
=