
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Г) хоча б на один із вантажних пунктів.Стр 1 из 2Следующая ⇒ Б)хоча б один вагон. Розв’язання: Якщо проводяться випробування, при яких появи події А в кожному випробуванні не залежить від початкових інших випробувань,то такі випробування називаються незалежними щодо події.Так як n мало, то застосовуємо формулу Бернулі. Ймовірність того, що в n незалежних випробувань, в кожному з котрих ймовірність появи події дорівнює p(0<p<1), подія наступить рівно k раз і дорівнює а) не більш 2-х, чи 0, чи 1, чи 2: Р(0 £ к £ 2) = Р4 (0) + Р4 (1) + P4 (2) = 0,4096 +0, 4096+0,1536 =0,9728, P1 = Р4 (0) = C04 Р0 g4 = 1×1× (0.8)4 = 0,4096, P2 = Р4 (1) = C 14 Р1 g3 = P3 = Р4 (2) = C24 Р2 g2 = б) хоча б 1 вагон: Р=1-Р4(0)=1-0,1096=0,5904.
2. У вокзальному приміщенні знаходиться каса, яка продає квитки на транзитні поїзди за годину до відправлення поїзду. При відсутності квитків каса зачинена. Матриця перехідних ймовірностей марківського процесу в такій обслуговуючій системі має вигляд: Знайти матрицю ймовірностей за два кроки. Дано:
Розв’язання Матриця ймовірностей переходу за два кроки Скориставшись формулою знаходимо:
Перемножив матриці відповідно знайдемо:
Відповідь:
3.В парку приймання чотири колії. Кількість колій, зайнятих в даний момент поїздами, які прибувають, є випадкова величина Х,яка розподілена за законом:
Знайти середню кількість зайнятих колій М(Х)  Розв’язання: Математичним сподіванням випадкової величини Х називається сума множення всіх її значень на відповідні ймовірності: М(Х)=Мх=х1р1+х2р2+……+хnpn= М(Х)= Мх=0*0,25+1*0,20+2*0,05+3*0,3+4*0,2=2 Висновок: середня кількість зайнятих колій дорівнює 2
4. Ймовірності появи в поїзді вагонів: на вантажний двір а) всі три пункти; б) на два пункти; в) на один пункт; г) хоча б на один із вантажних пунктів. Розв’язання: 1)Знайдемо подію,яка полягаєв ймовірністі появи в поїзді вагонів на всі три пункти: А=А1А2А3.Тобто Р=р1р2р3.Р=0,3*0,4*0,2=0,024 2)Ймовірність появи в поїзді вагонів на два пункти: В= А1А2А3+А1 Р=р1р2q3+р1q2p3+q1 p2p3 P=0.3*0.4*0.2+0.3*(1-0.4)*0.2+(1-0.3)*0.4*0.2=0.116 3) Ймовірність появи в поїзді вагонів на один пункт: C= А1 P= р1q2q3+q1p2q3+q1 q2p3 P=0.3*(1-0.4)*(1-0.2)+(1-0.3)*0.4*(1-0.2)+(1-0.3)*(1-0.4)*0.2=0.452 4) Ймовірність появи в поїзді вагонів хоча б на один із вантажних пунктів: D=1- P=1-q1q2q3 P=1-(1-0.3)*(1-0.4)*(1-0.2)=0,664
5. Дослідити ряд на збіжність Розв’язання: Поданий ряд –знакододатнім ряд. За ознакою Даламбера маємо:
Відповідь: ряд розбігається, так як
6. Виконати дії над матрицями:
Розв язання: 1. Множити можна матриці ,якщо число стовпців матриці А = числу рядків матриці В. Так як ця умова виконується, то використовуємо правило множення.( строку на стовбець)
2.
Відповідь:
7.У парку приймання 3 колії.Ймовірність зайнятості кожної з них поїздами,які прибувають,р=0,8.Знайти розподіл числа колій,зайнятих поїздами,які прибувають. По формулі Бернулі визначаємо імовірність появи події в n іспитах = k раз.
Т.я. у ПП 3 колій, то нехай випадкові величини приймають значення 0,1,2,3. Нехай k - кількість зайнятих колій, тоді закон розподіли буде представлений
P0(0)=
P3(0)= P3(1)= P3(2)= P3(3)=
8.Розв’язати систему рівнянь:
Розв’яжемо систему рівнянь за формулами Крамера:
Відповідь:
9. знайти невизначений інтеграл Розв’язання
Відповідь:
10.Знайти екстремум функції, інтервали зростання і спадання:
Розв язання: 1.Область визначення функції є (- 2.Знаходимо першу похідну функції:f’(х)=6х2-12х-18 Із рівняння 6х2-12х-18=0 знаходимо Д=144+432=576
х1= х2= 3.у’ існує при всіх х. 4.Визначаємо точки х1=3;х2=-1 на координатній прямій. Знайдемо як змінюються знаки похідної при переході скрізь точки стаціонарної функції.
-1 3 На інтервалі ,де х є х є (-1;3)-функція спадає х є (3;+ 5.З’ясували,що точка ( -1)-точка max;точка (-3)-min f(-1)=2*(-1)3-6(-1)2-18(-1)+9=19 f(3)=2*(3)3-6(3)2-18(3)+9=-45 6.На основі цих даних обераємо найменше і найбільше значення функції max f(х)= f (-1)=19 min f(х)= f(3)=-45 Відповідь:Zmin=-45;Zmax=19
11. Знайти границю функції Розв’язання: Оскільки
Відповідь:
12.Знайти похідну функції Розв’язання: Правило диференціювання добутку:
Диференціювання суми:
Відповідь:
13. Знайти загальний розв’язок Розв’язання: Складемо характеристичне рівняння:
За формулою: Загальний розв’язок однорідного рівняння має вигляд: Оскільки правою частиною даного рівняння є функція виду
Знайшовши похідні
Тому Відповідь:
14.Знайти частинні похідні Розв’язання: Згідно з означенням, при знаходженні частинної похідної Тому деференціруя дане рівняння, отримаємо:
Відповідь:
15. Знайти загальний розв’язок диференціального рівняння Розв’язання: Це диференціальне рівняння 1 го порядку з відокремлюваними змінними
Якщо змінні відокремлені то проінтегруемо обидві частини даного рівняння:
Відповідь:
16. Марковський ланцюг задано генератором Розв’язання: Граф має 2 сталі Е1,Е2.З матриці 3
4
Складемо рівняння Колмогорова: Припустимо: Тоді згідно формули
Помножуючи матриці в правій частині матричного рівняння і прирівнюючи елементи отриманої матриці відповідним елементам рядкової матриці в лівій частині одержемо:
- це система диференціальих рівнянь Колмогорова для знаходження стаціонарного розподілу достатньо в одержаній системі рівнянь покласти
Одне з рівнянь, нехай друге, залишимо на умову Звідси
Відповідь: так як стан Е1 і Е2 є суттєвим то знайдений розподіл збігається з фінальним розподілом ймовірностей станів, тобто
17.обчислити визначений інтеграл Розв’язання: Відповідь : 1
18. знайти площу трикутника АВС, якщо А(1;0;-2), В(1;-2;-1), С(0;1;-4) Дано: А(1;0;-2), В(1;-2;-1), С(0;1;-4) Знайти: Розв’язання: Розглянемо вектори
Знайдемо векторне помноження Проекція векторів
Модуль вектора знаходимо по формулі:
По формулі
Модуль вектора знайдемо по формулі
Відповідь: площа трикутника дорівнює 1,871
19.Знайти радіус та інтервал збіжності степеневого ряду Розв’язання: За радіальної формули Коші отримуємо
Тоді
1 нехай x=9
2. x=11
Відповідь:
20.Обчислити криволінійний інтеграл
Відповідь:
21.Знайти границю функції Розв’язання: На основі формули
Відповідь: е2
22.Розв’язати однорідну систему рівнянь:
Розв’язання: Визначаємо визначник системи:
Відповідь:так як
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 264. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 qn-k .
qn-k . ,
,



 дорівнює добуткові матриці ймовірностей за один крок на себе, тобто
дорівнює добуткові матриці ймовірностей за один крок на себе, тобто 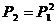






 , на контейнерну площадку
, на контейнерну площадку 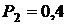 , на під’їзну колію
, на під’їзну колію 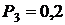 . Визначити ймовірність появи в поїзді вагонів на:
. Визначити ймовірність появи в поїзді вагонів на: .
. 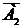
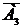 +
+  A2
A2  .
.


 ,якщо
,якщо  -ряд збігається, якщо
-ряд збігається, якщо  - ряд розбігається, якщо
- ряд розбігається, якщо 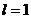 подана ознака не дає відповіді
подана ознака не дає відповіді



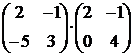 =
= 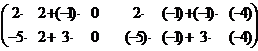 =
= 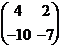
 .Множення матриці на число:
.Множення матриці на число: 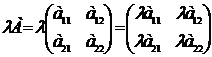
 =
= 
 =
= 

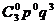


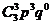
 P3(3)=
P3(3)= 
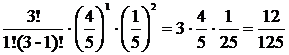






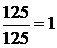




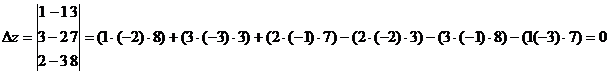
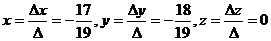





 ,тобто функція визначена при всіх х.
,тобто функція визначена при всіх х.
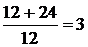
 х1=3;х2=-1
х1=3;х2=-1
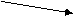
 max min
max min + - +
+ - + - функція зростає
- функція зростає -функція зростає
-функція зростає
 маємо невизначеність виду
маємо невизначеність виду 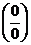 .Щоб розкрити невизначеність скористуємось правилом Лопиталя, маємо:
.Щоб розкрити невизначеність скористуємось правилом Лопиталя, маємо: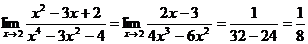

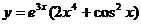




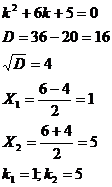


 ,причому
,причому  ,то частинний розв’язок шукаємо у вигляді
,то частинний розв’язок шукаємо у вигляді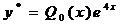 ,тобто
,тобто  , де А невідомий коефіцієнт
, де А невідомий коефіцієнт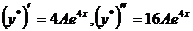 і підставивши їх у рівняння дістанемо:
і підставивши їх у рівняння дістанемо: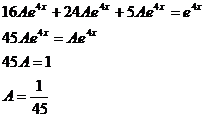
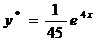 - частинний розв’язок даного рівняння, а
- частинний розв’язок даного рівняння, а 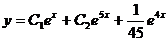
 функції
функції 
 обчислюють звичайну похідну функції однієї змінної вважаючи змінну y,сталою , а при знаходженні похідної
обчислюють звичайну похідну функції однієї змінної вважаючи змінну y,сталою , а при знаходженні похідної  сталою вважається змінна x.
сталою вважається змінна x.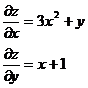
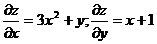



 - загальний розв’язок даного рівняння
- загальний розв’язок даного рівняння .Знайти фінальний розподіл ймовірностей станів.
.Знайти фінальний розподіл ймовірностей станів. знаходимо інтенсивність переходів
знаходимо інтенсивність переходів  і відмічаємо поряд з відповідними стілками:
і відмічаємо поряд з відповідними стілками: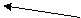 Е1
Е1


 матимемо
матимемо

 , а похідні
, а похідні 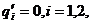 тоді:
тоді:
 тобто
тобто 
 ,отже стаціонарний розподіл такий
,отже стаціонарний розподіл такий

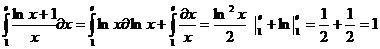

 і
і  .Площа трикутника АВС- це половина площі паралелограма. Побудованого на векторах
.Площа трикутника АВС- це половина площі паралелограма. Побудованого на векторах 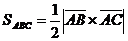
 , а тому половину його модуля.
, а тому половину його модуля.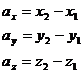
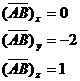



 для векторного помноження векторів знайдемо, що
для векторного помноження векторів знайдемо, що
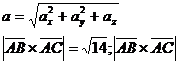


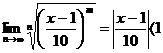

 - інтервал збіжності степеневого ряду
- інтервал збіжності степеневого ряду - ряд збігається
- ряд збігається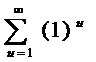 збігається
збігається радіус степеневого ряду
радіус степеневого ряду
 вздовж верхньої половини кола.
вздовж верхньої половини кола.




 .
.

 =
=  ,оскільки
,оскільки 

 =
=  =
= 
 ,то система має єдиний нульовий розв’язок: х=0;у=0;z=0
,то система має єдиний нульовий розв’язок: х=0;у=0;z=0