
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Физический смысл производной. ⇐ ПредыдущаяСтр 2 из 2 Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:
Уравнение касательной к графику функции y=f(x) в точке x0 :
35. Основные правила дифференцирования. Производная сложной и обратной функции. Производные элементарных функций. Логарифмическое дифференцирование. Основные правила дифференцирования. Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х. 1) (с)' = 0, (cu)' = cu'; 2) (u ± v)¢ = u¢± v¢3) (u×v)¢ = u×v¢ + u¢×v4) 5) если y = f(u), u=φ(x), т.е. y = f(φ(x)) - сложная функция (суперпозиция) которая составлена из дифференцируемых функций φ и f, то 6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), при этом Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу. Теорема.Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f. Тогда Производная обратной функции равна обратной величине производной данной функции. Теорема:( о существовании обратной функции):если функция y=f(x) непрерывна и строго монотонна на [a,b] оси Ох, то обратная функция также непрерывна и монотонна на соответствующем отрезке [c,d] оси Оу. Производные основных элементарных функций. 1)С¢ = 0;2)(xm)¢ = mxm-1;3) 8) 13) Логарифмическое дифференцирование. Рассмотрим функцию Тогда (lnïxï)¢=
Учитывая полученный результат, можно записать  Отношение Способ логарифмического дифференцированиясостоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким.
36. Дифференцируемость функций в точке. Дифференциал функции, его геометрический смысл и применение в приближенных вычислениях. Инвариантность формы дифференциала. Функция дифференцируема в точке тогда и только тогда, когда у неё существует конечная производная. Более того
Дифференциалом функции называется линейная относительно Геометрический смысл дифференциалаДифференциал функции в точке Применение дифференциала в приближенных вычислениях Установленное приближенное равенство Запишем приближенное равенство более подробно. Так как а Инвариантность формы дифференциала первого порядка Формула дифференциала функции имеет вид Пусть теперь дана сложная (дифференцируемая) функция так как
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 168. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


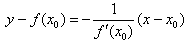 - нормаль к кривой
- нормаль к кривой , если v¹ 0
, если v¹ 0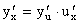 , или
, или 
 больше или меньше нуля, то
больше или меньше нуля, то 
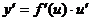
 4)
4)  5)
5) 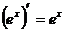 6)
6)  7)
7) 
 9)
9)  10)
10)  11)
11)  12)
12) 
 14)
14)  15)
15)  16)
16) 
 .
. , т.к.
, т.к. 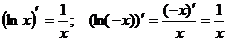 .
.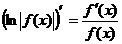 .
. называется логарифмической производной функции f(x).
называется логарифмической производной функции f(x).

 часть приращения функции. Она обозначается как
часть приращения функции. Она обозначается как 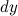 или
или 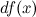 . Таким образом:
. Таким образом: 
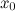 равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента
равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента  или
или 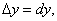 позволяет использовать дифференциал для приближенных вычислений значений функции.
позволяет использовать дифференциал для приближенных вычислений значений функции.
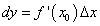 то
то  или
или 
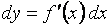 ,где
,где  - дифференциал независимой переменной.
- дифференциал независимой переменной.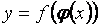 , где
, где  ,
,  . Тогда по формуле производной сложной функции находим
. Тогда по формуле производной сложной функции находим  ,
,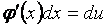 .Итак,
.Итак, 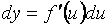 , т.е. формула дифференциала имеет один и тот же вид для независимой переменной
, т.е. формула дифференциала имеет один и тот же вид для независимой переменной  и для промежуточного аргумента
и для промежуточного аргумента 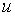 , представляющего собой дифференцируемую функцию от
, представляющего собой дифференцируемую функцию от