
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные числовые множестваСтр 1 из 2Следующая ⇒ Операции над множествами Два множества А и В равны (А=В), если они состоят из одних и тех же элементов. Объединением (суммой)множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств. Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В. Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В. Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА). Основные числовые множества Натуральные числа — числа, которые мы используем для счёта объектов. Множество натуральных чисел обозначается N Простые числа - натуральные числа, имеющие ровно два различных натуральных делителя: 1 и самого себя. Целые числа - множество целых чисел есть ноль и «плюс-минус натуральные». Рациональные числа - числа, которые можно представить дробью m/n, где m— целое число, а n— натуральное. Действительные (вещественные) числа - расширение множества рациональных чисел. Иррациональные числа — это все вещественные числа, которые не являются рациональными. Множество X  Множество X называется ограниченным снизу, если существует такое число a Множество, ограниченное сверху и снизу, называется ограниченным. Множество X называется неограниченным сверху, если для любого числа b Окре́стность точки — множество, содержащее данную точку, и близкие (в каком-либо смысле) к ней. Пусть задано топологическое пространство 24. Понятие функции. Способы задания функции. График функции. Обратная функция. Элементарные функции. Функция — это соответствие между двумя множествами, при котором каждому элементу одного множества соответствуетединственныйэлемент другого множества. Функцию можно задать несколькими способами: аналитическим (с помощью формулы), графическим, табличным, описанием с помощью словесной формулировки). График функции — множество точек, у которых абcциссы являются допустимыми значениями аргумента Функцию y=f(x), x∈X называют обратимой, если любое своё значение она принимает только в одной точке множества X (иными словами, если разным значениям аргумента соответствуют разные значения функции). Основными элементарными функциями являются: постоянная функция (константа), корень n-ой степени, степенная функция, показательная, логарифмическая функция, тригонометрические и обратные тригонометрические функции. 25. Числовая последовательность и ее предел. Бесконечно большие и бесконечно малые последовательности. Свойства сходящихся последовательностей. Числовой последовательностью называется бесконечное множество чисел x1, x2,…, xn, следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого xnзадается как функция целочисленного аргумента n, то есть xn = f(n) Теорема: Числовая последовательность не может иметь более одного предела. Число a называется пределом последовательности {xn} если для любого числа ԑ> 0 существует такой номер n0 = n0(ԑ), что при n ≥ n0 выполняется неравенство |xn – a| <ԑ. Теоремы: Предел суммы/разности двух последовательностей равен сумме/разности пределов от каждой из них, если последние существуют; Предел произведения двух последовательностей равен произведению пределов от каждой из них, если пределы сомножителей существуют; Предел отношения двух последовательностей равен отношению пределов от каждой из них, если эти пределы существуют и предел знаменателя не равен нулю; Последовательность Последовательность Последовательность называется сходящейся, если существует такое вещественное число а, что последовательность является бесконечно малой. При этомвещественноечисло а называется пределом последовательности Свойства сходящихся последовательностей 1)Если последовательность { an } сходится, то ее предел единственный.2) Если последовательность сходится, то она ограничена 3) Если последовательность { an } сходится к числу a
26. Монотонные последовательности. Теорема Вейерштрасса.Последовательность Последовательность Последовательность Теорема Вейерштрасса: Если последовательность 27. Второй замечательный предел. Число е.
28. Предел функции в точке (по Коши и по Гейне) и на бесконечности. Односторонние пределы функции. Бесконечно малые и бесконечно большие функции. Пусть задано некоторое числовое множество Число Число Рассмотрим функцию Число Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами. Число Число Функция Функция 29. Непрерывность функции в точке. Свойства функций, непрерывных в точке. Односторонняя непрерывность. Точки разрыва функций и их классификация. Непрерывность элементарных функций. Функция 1. функция 2. существует конечный предел функции 3. это предел равен значению функции в точке При нахождении предела функции Теорема1. Все основные элементарные функции непрерывны в каждой точке своей области определения. Теорема2. Пусть функции и Теорема3. Если Теорема4. Пусть функция Односторонняя непрерывность: Говорят, что функция непрерывна в точке справа (слева), если выполняется предельное соотношение: Точка 1. функция 2. существует конечный предел функции 3. это предел равен значению функции в точке называется точкой разрыва функции. Если в точке Если хотя б один из пределов Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции Функция называется элементарной, если она построена из конечного числа композиций и комбинаций Каждая элементарная функция, заданная в окрестности некоторой точки, непрерывна в этой точке. 30. Первый замечательный предел.
31. Три важных предела. 1 limx→∞(1+ax)bx=eab.limx→∞(1+ax)bx=eab.limx→0ln(1+x)x=1.limx→0ln(1+x)x=1. limx→0ex−1x=1.limx→0ex−1x=1.limx→0ax−1xlna=1,a>0,a≠1.limx→0ax−1xlna=1,a>0,a≠1. limx→0(1+x)a−1ax=1. 32. Сравнение бесконечно малых и бесконечно больших функций. Символы «о» и «О». Эквивалентные функции, их применение к вычислению пределов функций. Функция Функция Всякая бесконечно большая функция в окрестности точки х0 является неограниченной в этой окрестности. Функция Теорема: алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция. Теорема: произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая. Следствие: так как всякая б.м.ф. ограничена, то из теоремы вытекает произведение двух б.м.ф. есть функция бесконечно малая. Следствие: произведение б.м.ф. на число есть функция бесконечно малая. Теорема: частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая. Теорема: если функция - бесконечно малая, то обратная ей функция – бесконечно большая и наоборот. «O» большое и «o» малое — математические обозначения для сравнения асимптотического поведения функций. Это не равенство в обычном смысле, а несимметричное отношение Эквивалентные бесконечно малых функций необходимы если нужно находить границы без применения правила Лопиталя
33. Функции, непрерывные на отрезке и их свойства: теоремы Вейерштрасса, теорема Коши о прохождении функции через нуль, теорема Коши о промежуточном значении. Функция 1. Теорема Вейерштрасса. Если функция непрерывна на отрезке, то она достигает на этом отрезке свои наибольшее и наименьшее значения. 2. Непрерывная на отрезке 3. Теорема Больцано-Коши. Если функция 4. Если функция 34. Производная функции, ее геометрический и физический смысл. Односторонние производные. Уравнения касательной и нормали к кривой. Производной функции f(x) (f'(x0)) в точке x0 называется число, к которому стремится разностное отношение Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 195. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
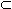 R называется ограниченным сверху, если существует такое число b
R называется ограниченным сверху, если существует такое число b  R, что для всех x
R, что для всех x 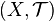 , где
, где 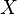 — произвольное множество, а
— произвольное множество, а 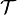 — определённая на
— определённая на 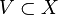 называется окрестностью точки
называется окрестностью точки  , если существует открытое множество
, если существует открытое множество 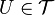 такое, что
такое, что 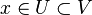 .
.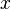 , а ординаты — соответствующими значениями функции
, а ординаты — соответствующими значениями функции 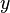 .
.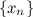 называется бесконечно малой последовательностью (б.м.п.), если для любого
называется бесконечно малой последовательностью (б.м.п.), если для любого 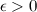 существует номер
существует номер 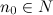 такой, что для любого
такой, что для любого 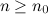 выполняется неравенство:
выполняется неравенство: 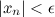
 существует номер
существует номер 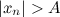
 0, то вся последовательность { an } лежит вне окрестности нуля
0, то вся последовательность { an } лежит вне окрестности нуля 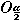 (0), начиная с некоторого номера. 4) Если для всех n, an
(0), начиная с некоторого номера. 4) Если для всех n, an  bn и
bn и 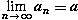 ,
, 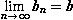 , то
, то 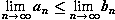 5) Если для всех n, xn
5) Если для всех n, xn 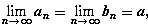 то
то 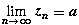
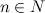 ,
, 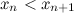
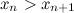
 где е - число Эйлера. Это число иррациональное и приближенно равно е = 2.718281828.... Логарифмы с основанием е называются натуральными
где е - число Эйлера. Это число иррациональное и приближенно равно е = 2.718281828.... Логарифмы с основанием е называются натуральными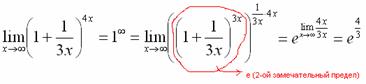
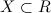 и каждому
и каждому 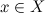 поставлено в соответствие число
поставлено в соответствие число 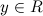 , тогда говорят, что на множестве
, тогда говорят, что на множестве  задана функция
задана функция 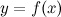 ,
,  называется пределом функции
называется пределом функции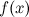 в точке
в точке  , если для
, если для 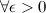
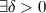 такое, что для
такое, что для 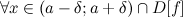 из того, что
из того, что 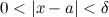 следует, что
следует, что 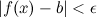 :
: 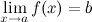 или
или 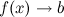 при
при 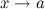 .
. , которая сходится к
, которая сходится к 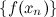 сходится к
сходится к 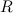 .
.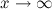 , если для любого
, если для любого 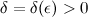 такое, что для всех
такое, что для всех  из того, что
из того, что 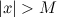 , выполняется неравенство
, выполняется неравенство 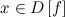 и
и  , выполняется неравенство
, выполняется неравенство 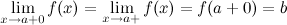
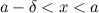 , выполняется неравенство
, выполняется неравенство 
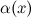 называется бесконечно малой функцией (б.м.ф.) при
называется бесконечно малой функцией (б.м.ф.) при 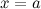 ), если
), если 
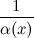 , обратная к б.м функции
, обратная к б.м функции 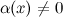 , есть функция бесконечно большая.
, есть функция бесконечно большая.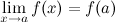

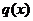 непрерывны Тогда функции
непрерывны Тогда функции  также непрерывны в точке
также непрерывны в точке 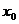 (последняя при условии, что
(последняя при условии, что 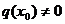 ).
). и функция
и функция 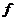 непрерывна в точке
непрерывна в точке 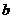 , то
, то 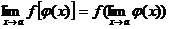 , или
, или  .
. непрерывна а функция
непрерывна а функция 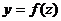 непрерывна в точке
непрерывна в точке  . Тогда сложенная функция
. Тогда сложенная функция  непрерывна в точке
непрерывна в точке 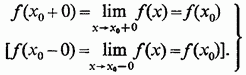 Если же то или другое из этих соотношений не осуществляется, то функция имеет в точке разрыв, соответственно, справа или слева.
Если же то или другое из этих соотношений не осуществляется, то функция имеет в точке разрыв, соответственно, справа или слева.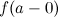 и
и 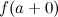 , такие, что
, такие, что 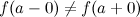 , то точка
, то точка 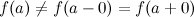 или функция
или функция 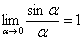 или
или 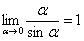
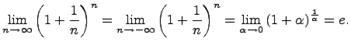
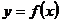 называется бесконечно большойпри
называется бесконечно большойпри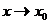 ,если для любого числа M>0 существует число
,если для любого числа M>0 существует число 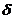 =
= 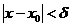 , выполняется неравенство
, выполняется неравенство 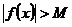 . Записывают
. Записывают  .
.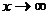 ,если для любого числа M>0 найдется такое число N=N (М)>0, что для всех х, удовлетворяющих неравенству
,если для любого числа M>0 найдется такое число N=N (М)>0, что для всех х, удовлетворяющих неравенству 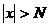 , выполняется неравенство
, выполняется неравенство 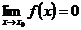 : для любого числа
: для любого числа 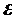 >0 найдется число
>0 найдется число 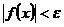 .
.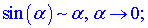
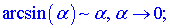
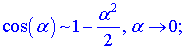

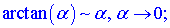

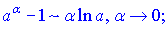
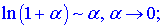
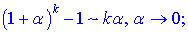
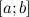 , если она является непрерывной в интервале
, если она является непрерывной в интервале 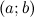 , непрерывной справа в точке
, непрерывной справа в точке 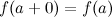 и непрерывной слева в точке
и непрерывной слева в точке 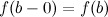 .
. ,
,  , то на этом отрезке функция принимает и все промежуточные значения между
, то на этом отрезке функция принимает и все промежуточные значения между  и
и 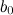 .
.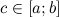 такая, что
такая, что 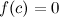 .
. , стремящемся к нулю.
, стремящемся к нулю.