Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение смешанной задачи для уравненияпараболического типа методом сеток Рассмотрим смешанную задачу для однородного уравнения теплопроводности. Задача состоит в отыскании функции u(x,t), удовлетворяющей в области
начальному условию
и граничным условиям первого рода
К задаче (3.1)-(3.3) приводит, в частности, задача о распространении тепла в однородном стержне длины а, на концах которого поддерживается заданный температурный режим. Граничные условия второго и третьего рода в данной лабораторной работе не рассматриваются. Замена переменных
поэтому в дальнейшем будем считать Построим в области D равномерную прямоугольную сетку с шагом
Рис.3.1.
Обозначим узлы сетки через Аппроксимируем уравнение (3.1) на четырехточечном шаблоне, который изображен на рис.3.1. (такой шаблон не единственный). В результате получаем неявную двухслойную разностную схему 
которая аппроксимирует уравнение (3.1) с погрешностью Схема (3.4) аппроксимирует уравнение (3.1) только во внутренних узлах сетки, поэтому число уравнений в схеме (3.4) меньше числа неизвестных
Схема (3.4)-(3.5) –неявная, поэтому значения Алгоритм численного решения задачи имеет следующий вид: на нулевом временном слое Применение неявной схемы при вычислениях обеспечивает ее устойчивость при любых значениях параметра l. Преимущества такой схемы особенно ощутимы при сравнении с явной схемой, которая получается при аппроксимации уравнения (3.1) на шаблоне, изображенном на рис.3.2.
Рис.3.2.
Явная схема оказывается устойчивой только при
Пример 3.1. Найти приближенное решение уравнения
Решение Выберем по аргументу х шаг
Так, при
Записываем полученные значения После этого переходим к вычислению значений на втором слое по формуле В двух последних строках таблицы 3.1 приведены значения точного решения
Таблица 1.
Пример 3.2. Методом прогонки найти решение уравнения
Решение
Возьмем Найдем значения Прямой ход. Записываем в строке
при j = 0 числа
Запишем по формулам
при
Результаты вычислений представлены в таблице 3.2.
Значения
Таблица 3.2.
Обратный ход. Из краевых условий получаем
при
………………………………………………………
Варианты заданий.
Решить смешанную задачу для уравнения теплопроводности
Литература
1. Самарский А.А. Теория разностных схем. - М.: Наука, 1990. 2. Тихонов А.Н., Самарский А.А. Уравнения математической физики. - М.: Наука, 1977. 3. Бахвалов Н.С. Численные методы. - М.: Наука, 1973. 4. Годунов С.К., Рябенький В.С., Разностные схемы. - М.: Наука, 1973. 5. Пискунов Н.С. Дифференциальное и интегральное исчисления. - М.: Наука, 1976. 6. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. - М.: Наука, 1972.
Содержание
1. Введение .............................................................................................. 3 2. Лабораторная работа №1. Решение задачи Дирихле для уравнения Лапласа методом сеток........................................................................ 5 3. Варианты заданий............................................................................. 10 4. Лабораторная работа №2. Решение смешанной задачи для уравне- ния гиперболического типа методом сеток ..................................... 11 5. Варианты заданий ............................................................................ 15 6. Лабораторная работа №3. Решение смешанной задачи для уравне- ния параболического типа методом сеток........................................ 16 7. варианты заданий ............................................................................. 23 Литература........................................................................................ 24
Учебное издание
Лабораторные работы по уравнениям математической физики для студентов строительных специальностей
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 423. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
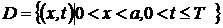 уравнению
уравнению
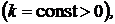
 (3.1)
(3.1) 
 . (3.3)
. (3.3) приводит уравнение (3.1) к виду
приводит уравнение (3.1) к виду ,
, .
. 
 , а приближенные значения функции
, а приближенные значения функции 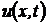 в этих узлах -
в этих узлах -  . Тогда
. Тогда  ,
,  ,
,  ,
,  ,
,  ,
,  .
. , (3.4)
, (3.4)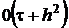 , причем
, причем 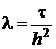 .
. . (3.5)
. (3.5) , если известно решение на временном слое
, если известно решение на временном слое  .
. решение известно из начального условия
решение известно из начального условия  . На каждом следующем слое искомая функция определяется как решение системы (3.4)-(3.5).
. На каждом следующем слое искомая функция определяется как решение системы (3.4)-(3.5).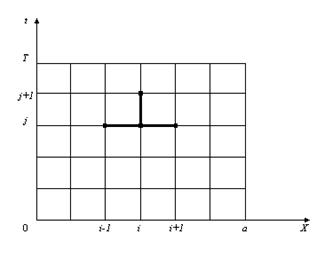
 , т.е. при
, т.е. при  . Это означает, что вычисления по явной схеме придется вести с очень малым шагом по t, что может привести к большим затратам машинного времени. В неявной схеме вычисления на одном шаге требуют больше операций, чем в явной схеме, но зато величину шага t можно выбрать как угодно большой без риска нарушить устойчивость схемы. Все это позволяет значительно уменьшить машинное время, необходимое для решения задачи. Схема (3.4) обладает сходимостью. Это означает, что при
. Это означает, что вычисления по явной схеме придется вести с очень малым шагом по t, что может привести к большим затратам машинного времени. В неявной схеме вычисления на одном шаге требуют больше операций, чем в явной схеме, но зато величину шага t можно выбрать как угодно большой без риска нарушить устойчивость схемы. Все это позволяет значительно уменьшить машинное время, необходимое для решения задачи. Схема (3.4) обладает сходимостью. Это означает, что при  , решение разностной задачи (3.4)-(3.5) стремиться к точному решению смешанной задачи (3.1)-(3.3).
, решение разностной задачи (3.4)-(3.5) стремиться к точному решению смешанной задачи (3.1)-(3.3). , удовлетворяющее условиям
, удовлетворяющее условиям 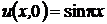
 и
и 
 .
. . Шаг по
. Шаг по  выберем
выберем 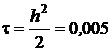 . Записываем в таблицу 3.1 начальные и краевые значения. Учитывая их симметрию, заполняем таблицу только для
. Записываем в таблицу 3.1 начальные и краевые значения. Учитывая их симметрию, заполняем таблицу только для  . Значения функции
. Значения функции  .
.
 . Таким образом, получаем
. Таким образом, получаем ,
, и т.д.
и т.д. во вторую строку таблицы 3.1.
во вторую строку таблицы 3.1. . Подобным образом определяем последовательно значения
. Подобным образом определяем последовательно значения  .
. задачи и модуля разности
задачи и модуля разности  при
при  , что говорит о точности предложенного метода.
, что говорит о точности предложенного метода.

 ,
,  ,
,  .
. и
и  .
. .
. таблицы 3.2 значения функции
таблицы 3.2 значения функции  , находим по формулам
, находим по формулам ;
;  ,
,  ,
, .
.
 ,
,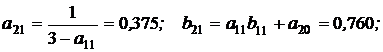
 и т.д.
и т.д. откуда
откуда 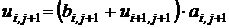 .
.
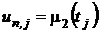 . Значения
. Значения  вычисляются по формулам
вычисляются по формулам


 .
. c начальным условием
c начальным условием