
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ГИПЕРБОЛИЧЕСКОГО ТИПА МЕТОДОМ СЕТОКСтр 1 из 3Следующая ⇒ Лабораторная работа№ 2 РЕШЕНИЕ СМЕШАННОЙ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА МЕТОДОМ СЕТОК
Рассмотрим смешанную задачу для однородного уравнения колебаний струны. Задача состоит в отыскании функции u(х, t), удовлетворяющей при t >0 уравнению
начальным условиям u (x, 0) = f (x),
и краевым условиям u (0, t) =
Так как замена переменных
то в дальнейшем будем считать с = 1. Для построения разностной схемы решения задачи (2.1) - (2.3) построим в области D = {(x, t)I, 0 ≤ x ≤ a, 0 ≤ t ≤ T} cетку хi = ih, i = 0, 1, …, n, a= = hn, tj = j τ, j = 0, 1, …, m, τm = T и аппроксимируем уравнение (2.1) в каждом внутреннем узле сетки на шаблоне типа «крест» (см. рис.1.1 лабораторной работы №1). Используя для аппроксимации частных производных центральные разностные производные, получим следующую разностную аппроксимацию уравнения (1.1):
Здесь ui,,j – приближенное значение функции u (x,t) в узле (хi, tj). Полагая ui,j+1 = 2(I - l2) u i,j + l2 (u i+1,j + ui –1,j) – u i,j-1, i = Для простоты зададим в данной лабораторной работе нулевые граничные условия, т.е. m1 (t) =0 и m2 (t) = 0. Значит, в схеме (2.5) Численное решение задачи состоит в вычислении приближенных значений  Для вычисления решения на первом слое (j = 1) в данной лабораторной работе принят простейший способ, состоящий в том, что если положить
то Описанная схема аппроксимирует задачу (2.1) – (2.3) с точностью 0 (t +h2). Невысокий порядок аппроксимации по t объясняется использованием слишком грубой аппроксимации для производной по t в формуле (2.6). Схема устойчива, если выполнено условие Куранта t < h. Это означает, что малые погрешности, возникающие, например, при вычислении решения на первом слое, не будут неограниченно возрастать при переходе к каждому новому временному слою. При выполнении условий Куранта схема обладает равномерной сходимостью, т.е. при (2.1) – (2.3). Недостаток схемы состоит в том, что как только выбрана величина шага сетки h в направлении х, появляется ограничение на величину шага t по переменной t. Если необходимо произвести вычисления для большого значения величины Т, то может потребоваться большое количество шагов по переменной t. Указанный недостаток характерен для всех явных разностных схем. Для оценки погрешности решения обычно прибегают к методам сгущения сетки. Пример. Для волнового уравнения решить смешанную задачу с начальными условиями
и нулевыми граничными условиями
Решение
Так как для явных разностных схем шаги сетки
Зная значение неизвестной функции в двух нижних слоях из соотношения (2.5), можно найти ее значение на следующем – третьем слое.
Поднявшись на одну строку вверх, аналогично, по схеме (2.5) вычисляется решение в последующий момент времени и т.д.:
u1,3 = 2(1 - l 2)u1,2 + l2(u2,2 + u0,2 ) – u1,1 » 0,336;
u2,3 = 2(1 - l2)u2,2 + l2(u3,2 +u1,2 ) – u2,1 » 0,348;
u1,4 = 2(1 - l2)u1,3 + l2(u2,3 + u0,3 ) – u1,2 » 0,322;
u2,4 = 2(1 - l2)u2,3 + l2(u3,3 + u1,3 ) – u2,2 » 0,337;
u1,5 = 2(1 - l2)u1,4 + l2(u2,4 + u0,4 ) – u1,3 » 0,301;
u2,5 = 2(1 - l2)u2,4 + l 2(u3,4 + u1,4 ) – u2,3 » 0,318. Варианты заданий Решить смешанную задачу для волнового уравнения с начальными условиями u (x, 0) = f (x),
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 613. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 0 < x < a, 0 < t ≤ T, (2.1)
0 < x < a, 0 < t ≤ T, (2.1) (x, 0) = g (x), 0 ≤ x ≤ a, (2.2)
(x, 0) = g (x), 0 ≤ x ≤ a, (2.2) u (a, t) =
u (a, t) =  . (2.3)
. (2.3)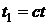 приводит уравнение (2.1) к виду
приводит уравнение (2.1) к виду ,
, . (2.4)
. (2.4)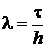 , получаем трехслойную разностную схему
, получаем трехслойную разностную схему (2.5)
(2.5) для всех
для всех  . Схема (2.5) называется трехслойной потому, что связывает между собой значения
. Схема (2.5) называется трехслойной потому, что связывает между собой значения  функции u (x,t) на трех временных слоях с номерами j –1, j, j +1. Схема (2.5) – явная, т.е. позволяет в явном виде выразить
функции u (x,t) на трех временных слоях с номерами j –1, j, j +1. Схема (2.5) – явная, т.е. позволяет в явном виде выразить  ,
, 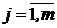 . Алгоритм решения основан на том, что решение на каждом следующем слое (j = 2, 3, …, n) можно получить пересчетом решений с двух предыдущих слоев (j =0, 1, …, n - 1) по формуле (2.5). На нулевом временном слое (j = 0) решение известно из начального условия
. Алгоритм решения основан на том, что решение на каждом следующем слое (j = 2, 3, …, n) можно получить пересчетом решений с двух предыдущих слоев (j =0, 1, …, n - 1) по формуле (2.5). На нулевом временном слое (j = 0) решение известно из начального условия 

 (2.6)
(2.6)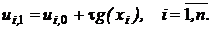 Тогда для вычисления решений на следующих слоях можно применять формулу (2.5). Решение на каждом следующем слое получается перерасчетом решений с двух предыдущих слоев по формуле (2.5).
Тогда для вычисления решений на следующих слоях можно применять формулу (2.5). Решение на каждом следующем слое получается перерасчетом решений с двух предыдущих слоев по формуле (2.5). решение разностной задачи равномерно стремится к решению исходной смешанной задачи
решение разностной задачи равномерно стремится к решению исходной смешанной задачи ,
,
 .
. и h (
и h (  , то взяв шаг, например
, то взяв шаг, например  , получим что
, получим что  неизвестной функции
неизвестной функции 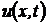 при j = 0 и j = 1 (в двух нижних временных слоях):
при j = 0 и j = 1 (в двух нижних временных слоях):
 .
.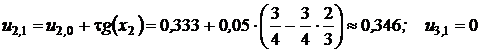 .
. 0,343;
0,343; 0,351.
0,351.
 xÎ[0;1] и нулевыми граничными условиями u (0, t) = u (1, t) = 0.
xÎ[0;1] и нулевыми граничными условиями u (0, t) = u (1, t) = 0.
 6
6








 7
7

 9
9