
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Площадь поверхности (с помощью двойного интеграла).Стр 1 из 2Следующая ⇒ РТФ ПРАКТИКА ВЕСНА 2015 (Неделя 1) Практика 1. 10.2.2015 Понятие первоообразной и неопределённого интеграла. Бесконечное множество первообразных, Раздача таблицы интегралов. Объяснение причины возникновения модуля в
Случаи D>0 и D<0 для дискриминанта знаменателя разложение на простейшие дроби либо выделение полного квадрата и сведение к arctg. Тригонометрические преобразования. Метод подведения под знак дифференциала. Практика 2. 14.2.2015 1. 5. 9. Интегрирование по частям: 10. (Неделя 2) Практика 3. 21.2.2015 1. 2. Вывод формулы 3. Рац.дроби. Все корни знаменателя различны: 5. 8. (Неделя 3) Практика 4. 24.2.2015 Кратные корни: 1. 2. Комплексные корни: 4. Иррациональности 6. Практика 5. 28.2.2015 Иррациональности: 1. Тригонометрические: 2. С помощью универсальной тригонометрической подстановки: 6. Иррациональности с применением тригонометрических замен: 7. Определённый интеграл. 9.
(Неделя 4) Практика 6. 7.3.2015 Определённый интеграл и его приложения 1.
5. 8. Найти S фигуры, ограниченной линиями 9. Пример с применением S для обратной функции для 10. Найти площадь области, ограниченной линиями
(Неделя 5) Практика 7. 14.3.2015  1. найти длину кривой 2. Найти длину 1 витка винтовой линии в пространстве 3. Найти объём тела, полученного вращением кривой 4. С помощью метода вычисления объёмов тел вращения, доказать формулу объёма конуса. 5. Найти несобственный интеграл 6. Найти несобственный интеграл 7. пример на повторение из прошлых тем. Контрольная работа 45 минут. Темы 1-й контрольной (14 марта) 1 Подведение под знак дифференциала, интегрирование по частям 2 Интегрирование рациональных дробей 3 Интегрирование иррациональностей и тригонометрических функций 4 Определённый интеграл, его приложения
(Неделя 6) Практика 8. 21.3.2015 Несобственный интеграл. Выяснить сходимость по признакам сравнения: Двойные интегралы в декартовых координатах. Вычисление. 1. 3. 4. Двойные интегралы в декартовых, описание области D. 1. Записать пределы интегрирования 2 способами для области, ограниченной кривыми 2. Изменить порядок интегрирования: 3. Изменить порядок интегрирования: Двойные интегралы в полярных. 1. Вычислить в полярных координатах 2. Вычислить в полярных координатах 3. Вычислить в полярных коорд интеграл по полукругу радиуса 1 в прав. полупл, f (x,y)= x. (2/3) 4. Записать в полярных координатах двойной интеграл по треугольнику с вершинами (0,0), (1,0), (1,1). Определим границы роста радиуса в зависимости от угла поворота. Для этого нужно задать линию x = 1 в полярных координатах. Подставим выражение x через полярные координаты в уравнение этой линии, получим (Неделя 7) Практика 9. 24.3.2015 Площадь поверхности (с помощью двойного интеграла). 1. Найти площадь поверхности 2. Доказать с помощью формулы площади поверхности, что площадь сферы равна Решение. Если из уравнения
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 225. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

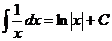

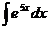



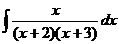

 решается преобразованием по формулам понижения степени.
решается преобразованием по формулам понижения степени.



 2.
2.  3.
3. 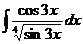 4.
4. 
 6.
6.  7.
7.  8.
8. 
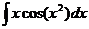
 11.
11.  12.
12.  13.
13.  14.
14. 
 Ответ
Ответ 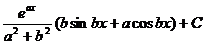
 для интегралов типа
для интегралов типа 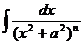 .
. 4.
4. 
 7.
7.  (отв. С равны 1/2, -1, 1/2)
(отв. С равны 1/2, -1, 1/2) 9.
9. 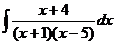 ((отв. С равны -0,5, 1,5) 10.
((отв. С равны -0,5, 1,5) 10. 
 (4/9, 5/3, 5/9)
(4/9, 5/3, 5/9) (0, -1, 1/2 , -1/2 ) 3.
(0, -1, 1/2 , -1/2 ) 3.  (1/4, 1/4, -1/4, 1/4).
(1/4, 1/4, -1/4, 1/4).  (коэф 1/4, -1/4, 0) 5.
(коэф 1/4, -1/4, 0) 5.  (коэф 1,1,1)
(коэф 1,1,1)  7.
7. 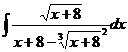 8.
8. 

 3.
3.  4.
4.  5.
5. 
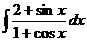
 8.
8. 

 10.
10. 
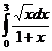 , 2.
, 2. 
 3.
3. 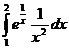 4.
4. 

 6.
6.  7.
7. 


 .
. 5/6
5/6 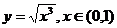


 вокруг оси 0x,
вокруг оси 0x,  отв
отв 
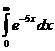 (1/5)
(1/5)


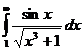
 (отв 1) 2.
(отв 1) 2.  (отв е-2)
(отв е-2) по треуг. (0,0),(1,0),(0,1) (1/3)
по треуг. (0,0),(1,0),(0,1) (1/3) по треуг-ку. (0,0),(1,1),(1,2)
по треуг-ку. (0,0),(1,1),(1,2)  ,
,  ,
,  .
.

 , где D - четверть круга радиуса 1
, где D - четверть круга радиуса 1 
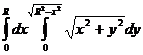

 , тогда
, тогда  .
.  Ответ:
Ответ: 
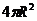 .
. сферы радиуса R выразить переменную z, то получим
сферы радиуса R выразить переменную z, то получим  , это уравнения верхней и нижней полусферы. Рассмотрим верхнюю полусферу:
, это уравнения верхней и нижней полусферы. Рассмотрим верхнюю полусферу:  и применим формулу площади явно заданной поверхности, то есть
и применим формулу площади явно заданной поверхности, то есть  . Здесь
. Здесь  ,
,  , подставим в формулу, получим
, подставим в формулу, получим 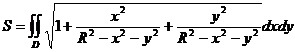 где D - круг радиуса R (проекция полусферы на плоскость Oxy, то есть область определения функции f). Далее, после преобразований получается
где D - круг радиуса R (проекция полусферы на плоскость Oxy, то есть область определения функции f). Далее, после преобразований получается  . Переходим к полярным координатам:
. Переходим к полярным координатам: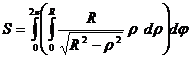 =
=  =
=  =
=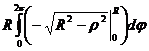 =
=  =
=  .
.