Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ АЛГОРИТМОВ
Алгоритм, составленный для некоторого исполнителя, можно представить различными способами: с помощью графического или словесного описания, в виде таблицы, последовательностью формул, записанным на алгоритмическом языке (языке программирования). Остановимся на графическом описании алгоритма, называемом блок-схемой. Этот способ имеет ряд преимуществ благодаря наглядности, обеспечивающей, в частности, высокую «читаемость» алгоритма и явное отображение управления в нем. Прежде всего определим понятие блок-схемы. Блок-схема - это ориентированный граф, указывающий порядок исполнения команд алгоритма; вершины такого графа могут быть одного из трех типов (рис. 1.12).
Рис. 1.12. Три типа вершин графа
На рис. 1.12 изображены «функциональная» (a) вершина (имеющая один вход и один выход); «предикатная» (б) вершина, имеющая один вход и два выхода (в этом случае функция Р передает управление по одной из ветвей в зависимости от значения Р (Т, т.е. true, означает «истина», F, т.е. false - «ложь»); «объединяющая» (в) вершина (вершина «слияния»), обеспечивающая передачу управления от одного из двух входов к выходу. Иногда вместо Т пишут «да» (либо знак +), вместо F- «нет» (либо знак -). Из данных элементарных блок-схем можно построить четыре блок-схемы (рис. 1.13), имеющих особое значение для практики алгоритмизации.
Рис. 1.13. Основные алгоритмические структуры
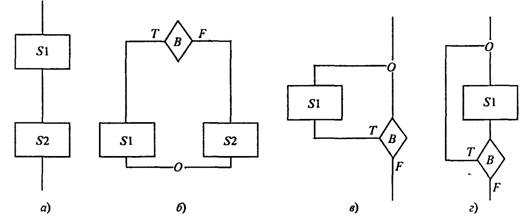
На рис. 1.13 изображены следующие блок-схемы: а -композиция, или следование; б -альтернатива, илиразвилка, в иг - блок-схемы, каждую из которых называютитерацией, илициклом (с предусловием (в), с постусловием (г)). S1 и S2 представляют собой в общем случае некоторые серии команд для соответствующего исполнителя, В - это условие, в зависимости от истинности (Т) или ложности (F) которого управление передаётся по одной из двух ветвей. Можно доказать, что для составления любого алгоритма достаточно представленных выше четырех блок-схем, если пользоваться их последовательностями и/или суперпозициями.  Блок-схема «альтернатива» может иметь и сокращенную форму, в которой отсутствует ветвь S2 (рис. 1.14, а). Развитием блок-схемы типа альтернатива является блок-схема «выбор» (рис. 1.14, б).
Рис. 1.14. Развитие структуры типа «альтернатива»; о) - неполная развилка; б) - структура «выбор»
На практике при составлении блок-схем оказывается удобным использовать и другие графические знаки (некоторые из них приведены на рис. 1.15).
Рис. 1.15. Некоторые дополнительные конструкции для изображения блок-схем алгоритмов СВОЙСТВА АЛГОРИТМОВ
Алгоритм должен быть составлен таким образом, чтобы исполнитель, в расчете на которого он создан, мог однозначно и точно следовать командам алгоритма и эффективно получать определенный результат. Это накладывает на записи алгоритмов ряд обязательных требований, суть которых вытекает, вообще говоря, из приведенного выше неформального толкования понятия алгоритма. Сформулируем эти требования в виде перечня свойств, которым должны удовлетворять алгоритмы, адресуемые заданному исполнителю. 1. Одно из первых требований, которое предъявляется к алгоритму, состоит в том, что описываемый процесс должен быть разбит на последовательность отдельных шагов. Возникающая в результате такого разбиения запись представляет собой упорядоченную совокупность четко разделенных друг от друга предписаний (директив, команд, операторов), образующих прерывную (или, как говорят, дискретную) структуру алгоритма. Только выполнив требования одного предписания, можно приступить к выполнению следующего. Дискретная структура алгоритмической записи может. Например, подчеркиваться сквозной нумерацией отдельных команд алгоритма, хотя это требование не является обязательным. Рассмотренное свойство алгоритмов называют дискретностью. 2. Используемые на практике алгоритмы составляются с ориентацией на определенного исполнителя. Чтобы составить для него алгоритм, нужно знать, какие команды этот исполнитель может понять и исполнить, а какие - не может. Мы знаем, что у каждого исполнителя имеется своя система команд. Очевидно, составляя запись алгоритма для определенного исполнителя, можно использовать лишь те команды, которые имеются в его СКИ. Это свойство алгоритмов будем называть понятностью. 3. Будучи понятным, алгоритм не должен содержать предписаний, смысл которых может восприниматься неоднозначно, т.е. одна и та же команда, будучи понятна разным исполнителям, после исполнения каждым из них должна давать одинаковый результат. Запись алгоритма должна быть настолько четкой, полной и продуманной в деталях, чтобы у исполнителя не могло возникнуть потребности в принятии решений, не предусмотренных составителем алгоритма. Говоря иначе, алгоритм не должен оставлять места для произвола исполнителя. Кроме того, в алгоритмах недопустимы также ситуации, когда после выполнения очередной команды алгоритма исполнителю неясно, какая из команд алгоритма должна выполняться на следующем шаге. Отмеченное свойства алгоритмов называютопределенностью илидетерминированностью. 4. Обязательное требование к алгоритмам -результативность. Смысл этого требования состоит в том, что при точном исполнении всех предписаний алгоритма процесс должен прекратиться за конечное число шагов и при этом должен получиться определенный результат. Вывод о том, что решения не существует - тоже результат. 5. Наиболее распространены алгоритмы, обеспечивающие решение не одной конкретной задачи, а некоторого класса задач данного типа. Это свойство алгоритма называютмассовостью. В простейшем случае массовость обеспечивает возможность использования различных исходных данных.
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 321. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |