
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Что такое математическое ожидание, дисперсия, средний квадрат дискретной величиныСтр 1 из 2Следующая ⇒ Контрольные вопросы 1.4.1. Что такое случайное событие? Определите события: достоверное, невозможное, противоположное, сумма событий, произведение событий, полная группа событий. Событие - всякий факт, который в результате опыта может произойти или не произойти. Вероятность события - это число, которое является мерой возможности реализации события. Вероятность P(A) случайного события A заключена в пределах Достоверное событие U такое, что Невозможное событие V такое, что Два события называются противоположными, если они несовместны и образуют полную группу. Событие, противоположное событию A, обозначается Суммой или объединением событий называется событие A, которое происходит тогда и только тогда, когда происходит, по крайней мере, одно из этих событий. Сумма обозначается
Произведением или пересечением событий
События
1.4.2. Что такое вероятность? Вероятность события - это число, которое является мерой возможности реализации события. Вероятность P(A) случайного события A заключена в пределах 1.4.3. Что такое условная вероятность? Каковы ее свойства? Условная вероятность — вероятность одного события при условии, что другое событие уже произошло. § Прямо из определения очевидно следует, что вероятность произведения двух событий равна:
§ Если 
1.4.4. Сформулируйте теорему умножения вероятностей. Теорема умножения вероятностей.Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое имело место:
1.4.5. Сформулируйте теорему сложения вероятностей. Теорема сложения вероятностей.Вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения:
1.4.6. Напишите формулу полной вероятности.
1.4.7. Напишите формулу Байеса.
1.4.8. Известны события A,B,C, причем A влечет за собой B. Определить: AB, A+B, ABC, A+B+C.
P(A + B) = P(A) + P(B) − P(AB) Р(АВС) = Р(А)*Р(В | А)*Р(С | АВ) P(A+B+C) = P(A)+P(B)+P(C)−P(AB)−P(AC)−P(BC)+P(ABC) 1.4.9. Система состоит из четырех приемников с непересекающимися сферами. Длительность сигнала такова, что он не может быть одновременно обнаружен двумя приемниками. Найти связь событий: A - сигнал обнаружен системой, ОтветP(Ai)= 0,25. 1.4.10.Прибор состоит из двух блоков первого типа и трех блоков второго типа. Определены события: P(Ai)=1/2. P(Bj)=1/3. Вероятность того что работает сразу 2 блока второго типа =(1-1/3)*1/3=2/9 Вероятность того что работает прибор =2/9*1/2=1/9 Ответ1/9. 1.4.11. Что является полным описанием дискретной случайной величины? Случайной величиной называется такая переменная величина, которая в результате опыта может принимать то или иное заранее неизвестное значение Дискретная случайная величина может принимать конечное или бесконечное множество значений Что такое математическое ожидание, дисперсия, средний квадрат дискретной величины Наиболее важными числовыми характеристиками случайной величины Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на их вероятности:
Дисперсией случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
1.4.13. Показать, что математическое ожидание суммы независимых случайных величин равно сумме математических ожиданий этих величин. M (X + Y) = M (X) + M (Y). Доказательство. Доказательство. Для упрощения вычислений ограничимся случаем, когда Х и Y принимают только по два возможных значения:
Тогда возможными значениями X + Y являются х1 + у1, х1 + у2,х2 + у1, х2 + у2. Обозначим их вероятности соответственно как р11, р12, р21 и р22. Найдем М( Х +Y) = (x1 + y1)p11 + (x1 + y2)p12 + (x2 + y1)p21 + (x2 + y2)p22 = = x1(p11 + p12) + x2(p21 + p22) + y1(p11 + p21) + y2(p12 + p22). Докажем, что р11 + р22 = р1. Действительно, событие, состоящее в том, что X + Y примет значения х1 + у1 или х1 + у2 и вероятность которого равна р11 + р22, совпадает с событием, заключающемся в том, что Х = х1 (его вероятность – р1). Аналогично доказывается, что p21 + p22= р2, p11 + p21 = g1, p12 + p22 = g2. Значит, M(X + Y) = x1p1 + x2p2 + y1g1 + y2g2 = M (X) + M (Y). 1.4.14. Показать, что математическое ожидание произведения независимых случайных величин равно произведению матожиданий этих величин. M(XY) = M(X)M(Y). Доказательство. Для упрощения вычислений ограничимся случаем, когда Х и Y принимают только по два возможных значения:
Тогда ряд распределения для XY выглядит так:
Следовательно, M(XY) = x1y1·p1g1 + x2y1·p2g1 + x1y2·p1g2 + x2y2·p2g2 = y1g1(x1p1 + x2p2) + +y2g2(x1p1 + x2p2) = (y1g1 + y2g2) (x1p1 + x2p2) = M(X)·M(Y). 1.4.15. Доказать, что дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин. D(X + Y) = D(X) + D(Y). Т.к.D(X) = M(X ²) – M ²(X). – свойство дисперсии Доказательство. D(X + Y) = M(X² + 2XY + Y²) – (M(X) + M(Y))² = M(X²) + 2M(X)M(Y) + M(Y²) – M²(X) – 2M(X)M(Y) – M²(Y) = (M(X²) – M²(X)) + (M(Y²) – M²(Y)) = D(X) + D(Y).
1.4.16. Вывести расчетное соотношение для дисперсии Ответ: 1.4.17. Показать, что для среднеарифметического независимых случайных величин |
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 248. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 .
.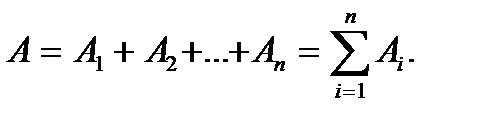

 называется такое событие A, которое происходит тогда и только тогда, когда происходят события вместе. Произведение обозначается
называется такое событие A, которое происходит тогда и только тогда, когда происходят события вместе. Произведение обозначается
 образуют полную группу событий, если в результате опыта появляется хотя бы одно из них:
образуют полную группу событий, если в результате опыта появляется хотя бы одно из них:

 , то изложенное определение условной вероятности неприменимо.
, то изложенное определение условной вероятности неприменимо.

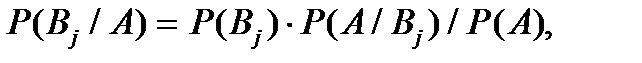

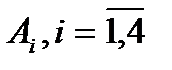 - сигнал обнаружен i-м приемником.
- сигнал обнаружен i-м приемником. - исправен i-й блок первого типа;
- исправен i-й блок первого типа;  - исправен j-й блок второго типа. Прибор исправен, если работает хотя бы один блок первого типа и не менее двух блоков второго типа. Выразить событие «Прибор работает» через события
- исправен j-й блок второго типа. Прибор исправен, если работает хотя бы один блок первого типа и не менее двух блоков второго типа. Выразить событие «Прибор работает» через события  и
и  .
. , из известного множества значений
, из известного множества значений  .
.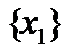 , которые можно пронумеровать
, которые можно пронумеровать 
 и законом распределения вероятностей
и законом распределения вероятностей  являются:
являются: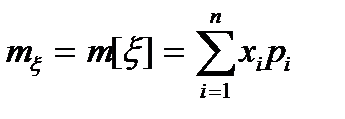 - математическое ожидание;
- математическое ожидание; - средний квадрат;
- средний квадрат; - дисперсия.
- дисперсия. через матожидание
через матожидание 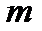 и средний квадрат
и средний квадрат  где
где  - возможные значения случайной величины;
- возможные значения случайной величины;  - вероятность этих значений.
- вероятность этих значений.
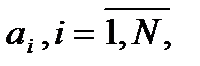 с одинаковыми средними
с одинаковыми средними  выполняются соотношения
выполняются соотношения 