
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Площадь криволинейного сектораСтр 1 из 2Следующая ⇒ Площадь криволинейной трапеции Криволинейной трапецией называется фигура, ограниченная графиком заданной на сегменте [a, b] непрерывной и неотрицательной фукнции f(x), ординатами, проведенными в точках a и b, и отрезком оси Ox между точками a и b (см. Рис. 2).
Докажем следующее утверждение. Криволинейная трапеция представляет собой квадрируемую фигуру, площадь P которой может быть вычислена по формуле
Доказательство. Так как непрерывная на сегменте [a, b] функция интегрируема, то для любого положительного числа ε можно указать такое разбиение Tсегмента [a, b], что разность S - s < ε, где S и s - соответственно верхняя и нижняя суммы разбиения T. Но S и s равны соответственно Sd и Si, где Sd и Si - площади ступенчатых фигур (многоугольников), первая из которых содержит криволинейную трапецию, а вторая содержится в криволинейной трапеции (на Рис. 2 изображены также и указанные ступенчатые фигуры). Так как Sd - Si < ε, то, в силу теоремы 1, криволинейная трапеция квадрируема. Поскольку предел при Δ → 0 верхних и нижних сумм равен Замечание. Если функция f(x) непрерывна и неположительна на сегменте [a, b], то значение интеграла Площадь криволинейного сектора  Пусть кривая L задана в полярной системе координат уравнением r = r(θ), α ≤ θ ≤ β (см. Рис. 3), причем функция r(θ) непрерывна и неотрицательна на сегменте [α, β]. Плоскую фигуру, ограниченную кривой L и двумя лучами, составляющими с полярной осью углы α и β, будем называть криволинейным сектором.
Докажем следующее утверждение. Криволинейный сектор представляет собой квадрируемую фигуру, площадь P которой может быть вычислена по формуле
Доказательство. Рассмотрим разбиение T сегмента [α, β] точками α = θ0 < θ1 < ... < θn = β и для каждого частичного сегмента [θi-1, θi] построим круговые секторы, радиусы которых равны минимальному ri и максимальному Ri значениям r(θ) на сегменте [θi-1, θi]. В результате получим две веерообразные фигуры, первая из которых содержится в криволинейном секторе, а вторая содержит криволинейный сектор (эти веерообразные фигуры изображены на Рис. 3). Площади
то, очевидно, Sd - Si < ε. В силу произвольности ε, отсюда вытекает квадрируемость криволинейного сектора. Из неравенств (3) вытекает справедливость формулы (2). 42 Вопрос: - 43 Вопрос: Метод прямоугольников — метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на многочлен нулевой степени, то есть константу, на каждом элементарном отрезке. Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближённом вычислении площади под графиком суммированием площадей конечного числа прямоугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота — значением подынтегральной функции в этих узлах. Алгебраический порядок точности равен 0. (Для формулы средних прямоугольников равен 1). Если отрезок 1. Формуле левых прямоугольников: 2. Формуле правых прямоугольников: 3. Формуле прямоугольников (средних): 44 Вопрос: Метод трапеций — метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольнымитрапециями. Алгебраический порядок точности равен 1. Если отрезок
Это простое применение формулы для площади трапеции — произведение полусуммы оснований, которыми в данном случае являются значения функции в крайних точках отрезка, на высоту (длину отрезка интегрирования). Погрешность аппроксимации можно оценить через максимум второй производной
Если отрезок
· Метод трапеций быстро сходится к точному значению интеграла для периодических функций, поскольку погрешность за период аннулируется. · Метод может быть получен путём вычисления среднего арифметического между результатами применения формул правых и левых прямоугольников. Метод пораболы: Формула Симпсона (также Ньютона-Симпсона[1]) относится к приёмам численного интегрирования. Получила название в честь британского математикаТомаса Симпсона (1710—1761). Суть метода заключается в приближении подынтегральной функции на отрезке Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке
где 45 Вопрос: 12.1. Несобственные интегралы по неограниченному промежутку (несобственные интегралы первого рода).
Критерий Коши: К. к. сходимости несобственных интегралов: пусть функция f определена на полуинтервале
сходился, необходимо и достаточно, чтобы для любого
Аналогичным образом критерий формулируется и для несобственных интегралов других типов, а также обобщается на случай, когда функция f зависит от нескольких переменных и ее значения лежат в банаховом пространстве.
Несобственный интеграл первого рода Свойства
Признак Абеля: Признак Абеля дает достаточные условия сходимости несобственного интеграла. Признак Абеля для несобственного интеграла I-рода (для бесконечного промежутка). Пусть функции 1. Функция 2. Функция Признак Абеля для несобственного интеграла II-рода (для функций с конечным числом разрывов). Пусть функции 1. Функция 2. Функция Признак Дирихле: Признак Дирихле — теорема, указывающая достаточные условия сходимости несобственных интегралов и суммируемости бесконечных рядов. Названа в честь немецкого математика Лежёна-Дирихле.
· Очевидно, что вместо второго условия можно также записать · Условие монотонности в признаке Дирихле существенно.
Однако, условие монотонности не является необходимым.
· Условие ограниченности первообразной в признаке Дирихле также является существенным, но не является необходимым. · Условная сходимость: Ряд · Если ряд условно сходится, то ряды, составленные из его положительных и отрицательных членов, расходятся. · Путём изменения порядка членов условно сходящегося ряда можно получить ряд, сходящийся к любой наперёд заданной сумме или же расходящийся (теорема Римана). · При почленном умножении двух условно сходящихся рядов может получиться расходящийся ряд. 47 Вопрос: Если функция не ограничена на промежутке интегрирования и промежуток интегрирования конечен, то определенный интеграл является несобственным интегралом второго рода. 1. Пусть функция y = f(x) определена и непрерывна на [a,b) и в точке b функция не ограничена. Если предел, стоящий справа, существует и конечен, то несобственный интеграл называется сходящимся и равен значению этого предела, в противном случае интеграл называется расходящимся. Если оба предела, стоящие в правой части, существуют и конечны, то несобственный интеграл называется сходящимся и он равен сумме этих пределов, в противном случае – расходящимся. Замечание 1. Несобственные интегралы могут быть комбинированного типа: первого и второго рода; или второго рода с несколькими точками разрыва второго рода. Замечание 2. Если функция на отрезке интегрирования терпит разрыв первого рода в точке с, то определенный интеграл от нее по этому отрезку не является несобственным, т.е. его можно свести к сумме двух обычных определенных интегралов. 49 Вопрос: Повт. Предел: Для функции нескольких переменных Пусть функция n переменных u = f(x) = f(x1, x2, … , xn) определена в некоторой окрестности точки Определение 1. Число A называется пределом функции f(x) в точке a = (a1, a2, … , an), если "ε > 0 $δ ε > 0 : x Î Oδ(a) Þ |f(x) − A| < ε Обозначение:
f(x) = A. В пространстве R2 предел функции f(x,y) в точке a(a1, a2) принято обозначать следующим образом:
f(x, y) = A. или
f(x, y) = A. Замечания. 1. Определение предела функции n переменных в точности совпадает с определением предела функции одной переменной, только окрестность точки a теперь не интервал (a − δ,a + δ), а n–мерный открытый шар (x1 − a1)2 + (x2 − a2)2 + … + (xn − an)2 < δ2. 2. Если a — граничная точка области определения D(f) функции f, то определение предела уточняется следующим образом (аналогично понятию одностороннего предела функции одной переменной): "ε >0 $δε > 0: x Î Oδ(a) ∩ D(f) Þ |f(x) − A|<ε. Теорема 1. Пусть функции n переменных f(x) и g(x), определены в области D Ì Rn и для некоторой точки a
f(x) = A и
g(x) = B. Тогда
[f(x) + g(x)] = A + B,
f(x) · g(x) = A · B, и при B ≠ 0
=
. Теорема доказывается так же, как для функции одной переменной. Определение 2. Функция f(x) называется бесконечно малой в точке a, если
f(x) = 0. Определения и теоремы о бесконечно малых функций одной переменной справедливы для бесконечно малых функций нескольких переменных. Вопрос: - 51 Вопрос: В математическом анализе, частная производная — одно из обобщений понятия производной на случай функции нескольких переменных. В явном виде частная производная функции
Следует обратить внимание, что обозначение Геометрически, частная производная является производной по направлению одной из координатных осей. Частная производная функции 52 Вопрос: Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке Пусть даны функции, определённые в окрестностях на числовой прямой,
Замечание[править] В обозначениях Лейбница цепное правило для вычисления производной функции
Инвариантность формы первого дифференциала[править] Дифференциал функции
где
Пусть теперь
Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет. Пусть
Дифференцируя эти функции отдельно:
получаем
В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления. Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению. Рассмотрим функцию
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате. Связь с градиентом Производную по направлению дифференцируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:
где 53 Вопрос: Для вычисления дифференциалов высших порядков используется следующая символическая формула:
Пример 8. z=y•lnx. Найти Найдем частные производные Пример 9. z=x2•y. Найти d3z Найдем частные производные
Подставив найденные частные производные в формулу для вычисления d3z, получим: d3z=0•dx3+3•2•dx2dy+3•0•dx2dy+0•dy3=6dx2dy Теорема: Смешанные частные производные одной и той же функции, отличающиеся лишь порядком (очерёдностью) дифференцирования, равны между собой при условии их непрерывности. Такое свойство называется равенством смешанных производных Определение смешанной производной[править] Пусть дана достаточно гладкая (скалярная) функция
Мы можем взять частную производную этой функции по одному из аргументов
Эта новая функция тоже зависит от остальных аргументов, как от параметров. То есть численное значение
Если функция
Если Основа теоремы[править] Для достаточно гладкой функции многих переменных значение смешанной производной не зависит от порядка дифференцирования:
Теорема является базовой в теории функций многих переменных и широко применяется в математической физике, теории дифференциальных уравнений в частных производных, дифференциальной геометрии. 54 Вопрос: Дифференциалом порядка n, где n > 1, от функции
Дифференциал высшего порядка функции одной переменной[править] Для функции, зависящей от одной переменной
Отсюда можно вывести общий вид дифференциала n-го порядка от функции
При вычислении дифференциалов высших порядков очень важно, что Дифференциал высшего порядка функции нескольких переменных[править] Если функция
Символически общий вид дифференциала n-го порядка от функции
где · С помощью дифференциалов, функция · для функции с одной переменной:
· для функции с несколькими переменными:
· Если первый дифференциал равен нулю, а второй дифференциал функции 55 Вопрос: Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум). Пусть дана функция ·
·
Если неравенства выше строгие, то ·
·
Значение функции Необходимые условия существования локальных экстремумов [править] · Из леммы Ферма вытекает следующее: Пусть точка Тогда либо производная (Математический Анализ. Том 1. Л. Д. Кудрявцев. Москва «Высшая Школа» 1973 г.) Достаточные условия существования локальных экстремумов [править] · Пусть функция
то Заметим, что при этом функция не дифференцируема в точке · Пусть функция
то · Пусть функция Если 56 Вопрос: Теорема о неявной функции — общее название для теорем, гарантирующих локальное существование и описывающих свойства неявной функции, т. е. функции
заданной уравнением
и значение Простейшая теорема о неявной функции состоит в следующем.
57 Вопрос: |
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 298. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 (1)
(1)
 и s ≤ P ≤ S, то площадь P криволинейной трапеции может быть найдена по формуле (1).
и s ≤ P ≤ S, то площадь P криволинейной трапеции может быть найдена по формуле (1).

 (2)
(2) и
и  указанных веерообразных фигур равны соответственно
указанных веерообразных фигур равны соответственно 
 и
и 
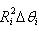 . Отметим, что первая из этих сумм является нижней суммойs для функции
. Отметим, что первая из этих сумм является нижней суммойs для функции  для указанного разбиения T сегмента [α, β], а вторая сумма является верхней суммой S для этой же функции и этого же разбиения. Так как функция
для указанного разбиения T сегмента [α, β], а вторая сумма является верхней суммой S для этой же функции и этого же разбиения. Так как функция 
 может быть как угодно малой. Например, для любого фиксированного ε > 0 эта разность может быть сделана меньше ε/2. Впишем теперь во внутреннюю веерообразную фигуру многоугольник Qi с площадью Si, для которого
может быть как угодно малой. Например, для любого фиксированного ε > 0 эта разность может быть сделана меньше ε/2. Впишем теперь во внутреннюю веерообразную фигуру многоугольник Qi с площадью Si, для которого 
 , и опишем вокруг внешней веерообразной фигуры многоугольник Qd площадью Sd, для которого
, и опишем вокруг внешней веерообразной фигуры многоугольник Qd площадью Sd, для которого 
 *. Очевидно, первый из этих многоугольников вписан в криволинейный сектор, а второй описан вокруг него. Так как справедливы неравенства
*. Очевидно, первый из этих многоугольников вписан в криволинейный сектор, а второй описан вокруг него. Так как справедливы неравенства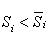


 (3)
(3) является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по
является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по


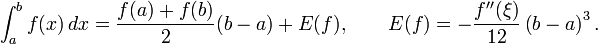


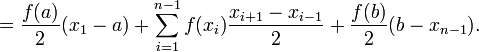
 интерполяционным многочленом второй степени
интерполяционным многочленом второй степени  , то есть приближение графика функции на отрезке параболой. Метод Симпсона имеет порядок погрешности 4 и алгебраический порядок точности 3.
, то есть приближение графика функции на отрезке параболой. Метод Симпсона имеет порядок погрешности 4 и алгебраический порядок точности 3.
 ,
,  и
и  — значения функции в соответствующих точках (на концах отрезка и в его середине).
— значения функции в соответствующих точках (на концах отрезка и в его середине). 12.1.1. Определение несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси
12.1.1. Определение несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси 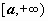 и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла
и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла  при
при  называется несобственным интегралом функции f(x) от a до
называется несобственным интегралом функции f(x) от a до  и обозначается
и обозначается  .
.  Итак, по определению,
Итак, по определению,  . Если этот предел существует и конечен, интеграл
. Если этот предел существует и конечен, интеграл  ; этот предел не существует; следовательно, исследуемый интеграл расходится.
; этот предел не существует; следовательно, исследуемый интеграл расходится. или
или  ), то интеграл сходится, в противном случае - расходится. При решении практических задач, однако, важно в первую очередь установить сам факт сходимости, и только затем вычислять интеграл (к тому же первообразная часто не выражается через элементарные функции). Сформулируем и докажем ряд теорем, которые позволяют устанавливать сходимость и расходимость несобственных интегралов от неотрицательных функций, не вычисляя их.
), то интеграл сходится, в противном случае - расходится. При решении практических задач, однако, важно в первую очередь установить сам факт сходимости, и только затем вычислять интеграл (к тому же первообразная часто не выражается через элементарные функции). Сформулируем и докажем ряд теорем, которые позволяют устанавливать сходимость и расходимость несобственных интегралов от неотрицательных функций, не вычисляя их.  удовлетворяют неравенствам
удовлетворяют неравенствам  . Тогда:
. Тогда:  , то сходится интеграл
, то сходится интеграл  ,
,  , то функции
, то функции  и
и  - монотонно возрастающие функции верхнего предела b (следствие свойств аддитивности и интегрирования неравенств). Монотонно возрастающая функция имеет конечный предел тогда и только тогда, когда она ограничена сверху. Пусть
- монотонно возрастающие функции верхнего предела b (следствие свойств аддитивности и интегрирования неравенств). Монотонно возрастающая функция имеет конечный предел тогда и только тогда, когда она ограничена сверху. Пусть 
 , F(b) ограничена, т.е.
, F(b) ограничена, т.е.  F(b) неограничена
F(b) неограничена  принимает на нем числовые значения и при любом
принимает на нем числовые значения и при любом  интегрируема (по Риману или по Лебегу) на отрезке [ а, с]. Для того чтобы несобственный интеграл
интегрируема (по Риману или по Лебегу) на отрезке [ а, с]. Для того чтобы несобственный интеграл
 существовало такое
существовало такое 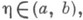 что для всех
что для всех  удовлетворяющих условию
удовлетворяющих условию  выполнялось неравенство
выполнялось неравенство
 называется сходящимся абсолютно, если сходится ряд из модулей
называется сходящимся абсолютно, если сходится ряд из модулей  , иначе — сходящимся условно.
, иначе — сходящимся условно.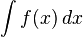 от функции сходится, то он называется сходящимся абсолютно или условно в зависимости от того, сходится или нет интеграл от ее модуля
от функции сходится, то он называется сходящимся абсолютно или условно в зависимости от того, сходится или нет интеграл от ее модуля 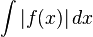 .
. называется абсолютно сходящимся, если сходится интеграл
называется абсолютно сходящимся, если сходится интеграл  .
. и
и  определены на промежутке
определены на промежутке 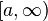 . Тогда несобственный интеграл
. Тогда несобственный интеграл  сходится, если выполнены следующие условия:
сходится, если выполнены следующие условия: . Тогда несобственный интеграл
. Тогда несобственный интеграл  сходится если выполнены следующие условия:
сходится если выполнены следующие условия:
 и имеет на
и имеет на  ограниченную первообразную
ограниченную первообразную  , то есть
, то есть  ;
· функция
;
· функция  ;
·
;
·  .
Тогда
.
Тогда  сходится.
сходится.
 .
.
 — сходится.
— сходится.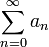 называется условно сходящимся, если сам он сходится, а ряд, составленный из абсолютных величин его членов, расходится. То есть, если
называется условно сходящимся, если сам он сходится, а ряд, составленный из абсолютных величин его членов, расходится. То есть, если  существует (и не бесконечен), но
существует (и не бесконечен), но  .
. .
.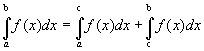 .
. можно определить понятие предела по одной из переменных
можно определить понятие предела по одной из переменных  при фиксированных значениях остальных переменных. В связи с этим возникает понятие повторного предела.
при фиксированных значениях остальных переменных. В связи с этим возникает понятие повторного предела. определяется следующим образом:
определяется следующим образом:
 следует понимать как цельный символ, в отличие от обычной производной функции одной переменной
следует понимать как цельный символ, в отличие от обычной производной функции одной переменной  , которую можно представить, как отношение дифференциалов функции и аргумента. Однако, и частную производную можно представить как отношение дифференциалов, но в этом случае необходимо обязательно указывать, по какой переменной осуществляется приращение функции:
, которую можно представить, как отношение дифференциалов функции и аргумента. Однако, и частную производную можно представить как отношение дифференциалов, но в этом случае необходимо обязательно указывать, по какой переменной осуществляется приращение функции:  , где
, где  — частный дифференциал функции
— частный дифференциал функции  . Часто непонимание факта цельности символа
. Часто непонимание факта цельности символа  в выражении
в выражении  . (подробнее см. Фихтенгольц, «Курс дифференциального и интегрального исчисления»).
. (подробнее см. Фихтенгольц, «Курс дифференциального и интегрального исчисления»). по координате
по координате  равна производной
равна производной  по направлению
по направлению  , где единица стоит на
, где единица стоит на  -ом месте.
-ом месте. , а функция g имеет производную в точке
, а функция g имеет производную в точке  , то сложная функция h(x) = g(f(x)) также имеет производную в точке
, то сложная функция h(x) = g(f(x)) также имеет производную в точке  где
где  и
и  Пусть также эти функции дифференцируемы:
Пусть также эти функции дифференцируемы:  Тогда их композиция также дифференцируема:
Тогда их композиция также дифференцируема:  и её производная имеет вид:
и её производная имеет вид:
 где
где  принимает следующий вид:
принимает следующий вид:
 в точке
в точке  имеет вид:
имеет вид:
 — дифференциал тождественного отображения
— дифференциал тождественного отображения  :
:
 Тогда
Тогда  , и согласно цепному правилу:
, и согласно цепному правилу:
 Тогда функция
Тогда функция 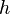 может быть записана в виде композиции
может быть записана в виде композиции 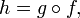 где
где




 от
от  аргументов в окрестности точки
аргументов в окрестности точки  . Для любого единичного вектора
. Для любого единичного вектора  определим производную функции
определим производную функции 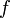 в точке
в точке  по направлению
по направлению  следующим образом:
следующим образом:
 ,
, — орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора
— орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора 

 . Дифференцируя повторно, получим
. Дифференцируя повторно, получим 


 , считая остальные аргументы постоянными параметрами. В результате мы получим новую функцию:
, считая остальные аргументы постоянными параметрами. В результате мы получим новую функцию: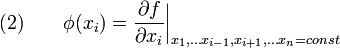
 в общем случае зависит от тех же переменных
в общем случае зависит от тех же переменных  , что и оригинальная функция
, что и оригинальная функция 
 :
:
 , то выражение в правой части равенства (4) называется смешанной производной.
, то выражение в правой части равенства (4) называется смешанной производной.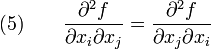
 в некоторой точке называется дифференциал в этой точке от дифференциала порядка (n — 1), то есть
в некоторой точке называется дифференциал в этой точке от дифференциала порядка (n — 1), то есть .
. второй и третий дифференциалы выглядят так:
второй и третий дифференциалы выглядят так:


 есть произвольное и не зависящее от
есть произвольное и не зависящее от  имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так:
имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так:  .
.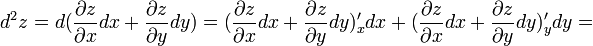
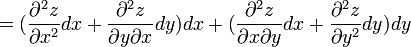
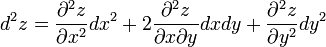

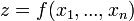 выглядит следующим образом:
выглядит следующим образом:
 , а
, а  произвольные приращения независимых переменных
произвольные приращения независимых переменных  .
.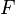 при условии существования её (n + 1) первых производных может быть представлена по формуле Тейлора:
при условии существования её (n + 1) первых производных может быть представлена по формуле Тейлора: ,
,  ;
; ,
,  явлется положительно определённым (отрицательно определенным), то точка
явлется положительно определённым (отрицательно определенным), то точка  является точкой строгого минимума (соответственно строгого максимума); если же второй дифференциал функции
является точкой строгого минимума (соответственно строгого максимума); если же второй дифференциал функции  и
и  — внутренняя точка области определения
— внутренняя точка области определения 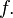 Тогда
Тогда если существует проколотая окрестность
если существует проколотая окрестность  такая, что
такая, что

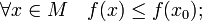

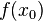 называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.
называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума. не существует, либо
не существует, либо  .
. непрерывна в
непрерывна в  и существуют конечные или бесконечные односторонние производные
и существуют конечные или бесконечные односторонние производные  . Тогда при условии
. Тогда при условии

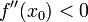

 раз в точке
раз в точке  , а
, а 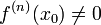 .
. , то
, то  , то
, то  ,
,  ,
, ,
, 
 фиксированно.
фиксированно. · непрерывна в некоторой окрестности точки
· непрерывна в некоторой окрестности точки 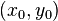 ·
·  и
· при фиксированном x функция F(x,y) строго монотонна по y в данной окрестности,
тогда найдётся такой двумерный промежуток
и
· при фиксированном x функция F(x,y) строго монотонна по y в данной окрестности,
тогда найдётся такой двумерный промежуток 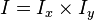 , являющийся окрестностью точки
, являющийся окрестностью точки  , что для любой точки
, что для любой точки 

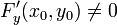 , здесь
, здесь  обозначаетчастную производную
обозначаетчастную производную  . Более того, в этом случае производная функции
. Более того, в этом случае производная функции 