
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Средняя квадратическая погрешность арифметической срединыПусть точность результатов измерений l1, l2, …, ln характеризуется средними квадратическими погрешностями m1 = m2 = ¼ = mn = m и требуется найти среднюю квадратическую погрешность M арифметической средины. Представим формулу (9.11) в следующем виде: L = Среднюю квадратическую погрешность арифметической средины найдем как погрешность функции измеренных величин по формуле (9.10)
или Формула (9.15) показывает, что погрешность арифметической средины с ростом числа измерений убывает пропорционально квадратному корню из этого числа. Так, чтобы погрешность среднего арифметического уменьшить в 2 раза, число измерений надо увеличить в 4 раза. Обработка результатов равноточных измерений Математическая обработка ряда результатов l1, l2, …, ln прямых равноточных измерений одной величины выполняется в следующей последовательности: 1. Вычисляют среднее арифметическое L L = 2. Вычисляют поправки к vi результатам измерений Контролем правильности вычислений служит сумма поправок, которая должна быть близка к нулю. 3. Вычисляют среднюю квадратическую погрешность одного измерения по формуле Бесселя:  Значение m вычисляют с двумя-тремя значащими цифрами. Вычисляют среднюю квадратическую погрешность среднего арифметического Математическая обработка результатов прямых неравноточных измерений Веса измерений. Неравноточными называют измерения, выполненные приборами различной точности, разным числом приемов, в различных условиях. При неравноточных измерениях точность каждого результата измерений характеризуется своей среднеквадратической погрешностью. Наряду со средней квадратической погрешностью при обработке неравноточных измерений пользуются относительной характеристикой точности – весом измерения. Вес i-го измерения вычисляют по формуле где с – произвольная постоянная, назначаемая вычислителем, mi – средняя квадратическая погрешность i-го измерения. Так, имея ряд результатов измерений l1, l2, ..., ln , со средними квадратическими погрешностями m1 , m2 , ..., mn , определяют их веса: p1 = c / m12, p2 = c / m22 , ..., pn = c / mn2. (9.21) Часто постоянную с для удобства дальнейших вычислений назначают так, чтобы веса pi оказались целыми числами. Рассмотрим смысл произвольной постоянной с. Предположим, что в результате фиксирования значения с вес j-го измерения стал равен 1, то есть pj = c / mj2 = 1. Отсюда находим c = mj2. Следовательно, постоянная с есть квадрат средней квадратической погрешности m2 такого измерения, вес которого принят за единицу (с = m2). Теперь (9/20) можем записать так
Кратко m называют средней квадратической погрешностью единицы веса. РАЗДЕЛ 3. ГЕОДЕЗИЧЕСКИЕ ИЗЫСКАНИЯ И ТОПОГРАФИЧЕСКАЯ СЪЁМКА
ЛЕКЦИЯ 10 ИЗМЕРЕНИЯ ГОРИЗОНТАЛЬНЫХ УГЛОВ И МАГНИТНЫХ НАПРАВЛЕНИЙ ПРИ ПОМОЩИ БУССОЛЕЙ, ГОНИОМЕТРОВ. ИЗМЕРЕНИЯ ПРИ ПОМОЩИ ЭКЕРОВ И ЭКЛИМЕТРОВ
10. 1 Измерения горизонтальных и вертикальных углов |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 516. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . (9.13)
. (9.13)
 (9.14)
(9.14)
 9.15)
9.15)
 (i = 1, 2, …, n) (9.17)
(i = 1, 2, …, n) (9.17)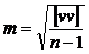 . (9.18)
. (9.18) . (9.19)
. (9.19) (9.20)
(9.20) (9.10)
(9.10)