
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Условие параллельности прямой и плоскости ⇐ ПредыдущаяСтр 2 из 2 Прямая и плоскость параллельны, если скалярное произведение направляющего вектора Условие параллельности прямой и плоскости (Рис. 3):
Рис. 3 Условие перпендикулярности прямой и плоскости Прямая и плоскость перпендикулярны, если направляющий вектор Условие перпендикулярности прямой и плоскости (Рис. 4):
Рис. 4 Условие принадлежности прямой плоскости Условие принадлежности прямой плоскости (Рис. 5):
Рис. 5 Точка пресечения прямой с плоскостью Точка пресечения прямой с плоскостью:
Чтобы решить систему, нужно от канонических уравнений прямой перейти к параметрическим уравнениям:
Подставляя эти выражения для x, y, z в уравнение плоскости, определяем параметр t.
Подставляя найденное значение t в параметрическое уравнение, получаем координаты искомой точки пересечения прямой и плоскости.
Задачи Задача 1. Найти угол между прямой Решение Запишем уравнения данной прямой в виде Таким образом,
Задача 2. Составить параметрические уравнения прямой, проходящей через точку Решение Так как нормальный вектор При
Задача 4. Найти точку пересечения прямой  Решение Запишем уравнение прямой в параметрическом виде: Подставляя теперь это значение t в параметрические уравнения прямой, находим координаты точки пересечения: Задача 6. Дана прямая Решение Составим уравнение плоскости, проходящей через точку M перпендикулярной к данной прямой. Найдем точку Q, в которой эта плоскость пересекает данную прямую. Запишем уравнения прямой в параметрическом виде: Подставляя x, y, z в уравнение плоскости, получим Точка Q имеет координаты
Откуда
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 170. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 прямой и нормального вектора
прямой и нормального вектора 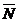 плоскости равно нулю.
плоскости равно нулю.

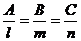
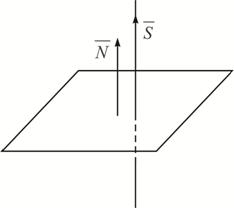



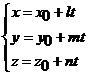 .
.
 ,
, 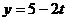 ,
,  и плоскостью
и плоскостью  .
. . Теперь, используя формулу (1) при
. Теперь, используя формулу (1) при  ,
,  ,
,  ,
,  ,
,  ,
,  , получим
, получим  .
. .
. и перпендикулярной плоскости
и перпендикулярной плоскости 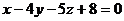 . Найти точку M прямой, соответствующую значению параметра
. Найти точку M прямой, соответствующую значению параметра  .
. данной плоскости перпендикулярен ей, то по условию он должен быть параллелен искомой прямой. Так как
данной плоскости перпендикулярен ей, то по условию он должен быть параллелен искомой прямой. Так как 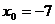 ,
,  ,
,  ,
,  ,
,  , получаем параметрические уравнения прямой:
, получаем параметрические уравнения прямой:  .
. ,
,  ,
,  , т. е. получаем точку
, т. е. получаем точку 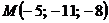 .
. с плоскостью
с плоскостью  .
. ,
,  ,
,  . Подставляя значения x, y, z в уравнение плоскости, имеем
. Подставляя значения x, y, z в уравнение плоскости, имеем  , откуда
, откуда 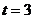 .
. ,
,  ,
,  ,
,  .
. и вне ее точка
и вне ее точка  . Найти точку N, симметричную M относительно данной прямой.
. Найти точку N, симметричную M относительно данной прямой. или
или  .
. ,
,  ,
,  ,
,  ,
,  .
. . Тогда координаты симметричной точки можно найти из формул координат середины отрезка, т. е.
. Тогда координаты симметричной точки можно найти из формул координат середины отрезка, т. е.  ;
; 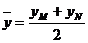 ;
; 
 ;
;  ;
;  .
. ;
;  ;
; 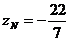 . Следовательно,
. Следовательно,  .
.