
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Результаты работы программыСтр 1 из 2Следующая ⇒ Кафедра «Космические исследования»
КУРСОВОЙПРОЕКТ Численное решение краевых задач для обыкновенных дифференциальных уравнений второго порядка Вариант - 2C по дисциплине «Численные методы и математическое моделирование»
Выполнил студент гр.23412/1 Тихоненко Д.И.
<подпись> Руководитель доцент, к.ф.-м.н. Веселова И.Ю.
<подпись>
«___» __________ 2017 г.
Санкт-Петербург 2017 Оглавление 1. Решение краевой задачи для обыкновенного дифференциального уравнения второго порядка 1.1 Постановка задачи (конкретный вариант). 1.2. Вывод разностной схемы для уравнения и граничных условий 1.3 Вывод выражения для главного члена погрешности аппроксимации уравнения и граничных условий 1.4 Тестовые задачи с нулевой и не нулевой погрешностью аппроксимации 1.5 Текст программы 1.6 Результаты работы программы 1.7 Выводы 2. Решение задачи на собственные значения для обыкновенного дифференциального уравнения второго порядка  2.1 Постановка задачи (конкретный вариант). 2.2 Вывод разностной схемы для уравнения и граничных условий 2.3 Алгебраическая формулировка обобщённой задачи на собственные значения. Вид коэффициентов матриц 2.4 Приведение обобщённой алгебраической задачи на собственные значения к классическому виду. Вид коэффициентов матрицы в классической формулировке 2.5 Аналитическое решение тестовой задачи для 2.6 Текст программы 2.7 Результаты работы программы 2.8 Выводы
Часть I Решение краевой задачи для обыкновенного дифференциального уравнения второго порядка 1.1 Постановка задачи (вариант 2C):
1.2 Вывод разностной схемы для уравнения и граничных условий:
Введём равномерную сетку :
Введем вспомогательную сетку:
Посчитаем уравнение по формуле средних прямоугольников во внутренних точках:
По этой формуле:
Посчитаем уравнение по формуле левых прямоугольников для левой границы:
Аппроксимация граничного условия второго рода на правой границе:
Витоге получим разностную схему длякраевой задачи для обыкновенного дифференциального уравнения второго порядка. Система из N+1 алгебраических уравнений:
Данная система является 3-х диагональной,приведём подобные члены в уравнениях разностной схемы при
Элементы нижней диагонали матрицы А - главной диагонали - верхней диагонали - правой части -
Вывод выражения для главного члена погрешности аппроксимации уравнения и граничных условий. Итак,мы свели краевую задачу к алгебраической задаче вида: Av=B, где A-матрица коэффициентов разностной схемы, В-вектор коэффициентов правой части, v-вектор точных решений системы Av=B
Общая погрешность решения краевой задачи складывается из погрешности аппроксимации и погрешности решения системы алгебраических уравнений.Рассмотрим подробнее погрешность аппроксимации уравнения.
Вычислим невязку
Подставляем точное решение вместо приближённого и ищем невязку:
1.4 Тестовые задачи: А)Тестовая задача с нулевой погрешностью аппроксимации: Пусть u(r)=const=1 , k(r)=1 , q(r)=1 Подставим u,k,q в (1),(2),(3) Тогда,получим что
Б)Тестовая задача с ненулевой погрешностью аппроксимации: Пусть Тогда используя (1),(2) и (3) получим,что
1.5 Код программы на фортране:
Результаты работы программы Таблица результатов работы программы на тестах (зависимость Чебышёвской нормы погрешности решения от удваивающегося количества разбиений
Табл. 1
Табл. 2.
Табл. 3
Выводы По таблице 1 можно увидеть зависимость погрешности решения системы алгебраических уравнений функцией LSLTR от количества разбиений, т.к. для тестовой задачи с нулевой невязкой решение будет найдено с машинной погрешностью и погрешностью решения алгебраических уравнений. Видим, что с увеличением числа разбиений погрешность решения системы увеличивается. Это объясняется тем, что обусловленность матрицы растёт при росте количества узлов. Из таблицы 2 мы видим, что погрешность уменьшается примерно в 4 раза при увеличении числа разбиений в 2 раза, т.е. разностная схема имеет 2 порядок аппроксимации по h. Из таблицы 3 видим, что разность численного решения вi-ых узлах при шаге h и h/2 примерно в 4 раза больше разности численного решения в тех же узлах при шаге h/2 и h/4, следовательно, разностная схема имеет 2 порядок аппроксимации по h.
Часть II |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 264. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и 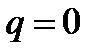

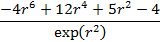







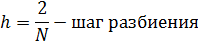



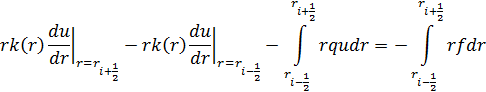




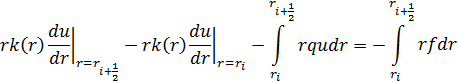









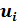 -ых:
-ых:
 ,
, ,
, ,
,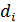



 -вектор приближённых решений системы.
-вектор приближённых решений системы.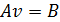

 ,
,  -невязка
-невязка





 ,
, 










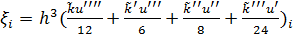 (1)
(1)
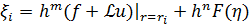










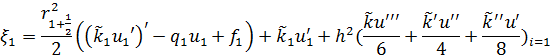


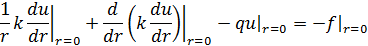
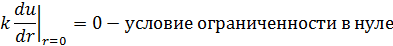

 (2)
(2)





 (3)
(3)



 f(r)=1
f(r)=1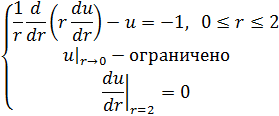


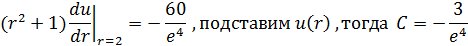




 ,N=10). Для нулевой погрешности (таблица 1) и для ненулевой погрешности (таблица 2)
,N=10). Для нулевой погрешности (таблица 1) и для ненулевой погрешности (таблица 2)







