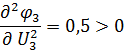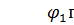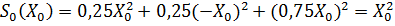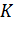Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задание №3. Оптимизация дискретных управлений дискретными динамическими объектами методом динамического программирования Р. БеллманаСтр 1 из 2Следующая ⇒ Исходные данные Кзаданию №1.
Кзаданию №2.
К заданию №3.
К заданию №4.
К заданию №5.
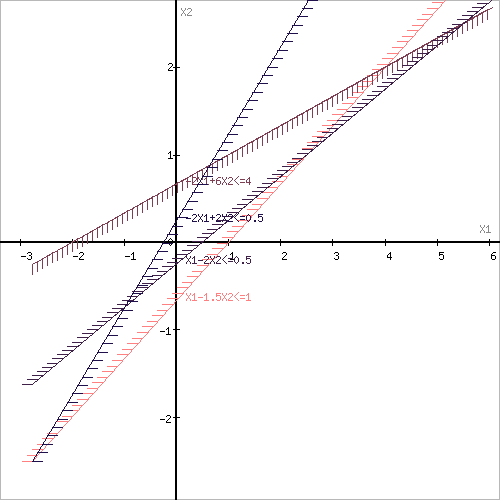
Задание №1. Графоаналитическое решение ОЗЛП 1. Математическая постановка ОЗЛП: φ=3x1+4x2→max, (0) x1-1,5x2≤1, (1) -2x1+6x2≤4, (2) x1-2x2≤0,5, (3) -2x1+2x2≤0,5, (4) x1≥0, (5) x2≥0, (6) EF: x1-1,5x2=1, (1’) DF: -2x1+6x2=4, (2’) CE: x1-2x2=0,5, (3’) BD: -2x1+2x2=0,5, (4’) AC: x1=0, (5’) AB: x2=0, (6’) 2. Записываем уравнение граничных линий допустимого многоугольника(1’) - (6’). На плоскости (x1, x2) строим граничные линии. 3. Строим линию, пересекающую область φ.
4. Находим градиент целевой функции:
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника решений.
Рассмотрим целевую функцию задачи φ=3x1+4x2→max. Построим прямую, отвечающую значению функции φ=0: F=3x1+4x2=0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0;0), конец – точка (3;4). Будем двигать эту прямую параллельным образом до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией. 
Из рисунка видно, что оптимальная точка F* равная
Ответ:
Задание № 2. Задача о коммивояжере. Метод ветвей и границ Расстояния между пунктами заданы матрицей:
Решение задачи о коммивояжере методом ветвей и границ начинается с приведения матрицы (вычитания из каждой строки (столбца) матрицы C минимального элемента этой строки (столбца). Произведем приведение матрицы Cпо строкам: hν=min(i) hνi
Произведем приведение матрицы Cпо столбцам: gi = min(υ) gνi
В итоге получаем полностью приведенную (редуцированную) матрицу:
Величины hν и gi называются константами приведения. Нижняя граница цикла: d0=6 ( Шаг №1. Определяем ребро ветвления и разобьем все множество допустимых значений Q0 относительно этого ребра на два непересекающихся подмножества ( В приведенной матрице исследуем все нулевые переходы.
Наибольшая сумма констант приведения равна υ15=α1+ β5=2+2=4, следовательно, множество разбивается на два подмножества Оценка длины цикла: В результате получим другую сокращенную матрицу (5x5), которая подлежит операции приведения. После операции приведения сокращенная матрица будет иметь вид:
d1=0 Шаг №2. Определяем ребро ветвления и разобьем все множество допустимых значений Q1 относительно этого ребра на два непересекающихся подмножества В приведенной матрице исследуем все нулевые переходы.
Наибольшая сумма констант приведения равна υ43=2+2=4, следовательно, множество разбивается на два подмножества Оценка длины цикла: Оценка на перспективном множестве: В результате получим другую сокращенную матрицу (4x4), которая подлежит операции приведения.
После операции приведения сокращенная матрица будет иметь вид:
d2=0 Шаг №3. Определяем ребро ветвления и разобьем все множество допустимых значений Q2относительно этого ребра на два непересекающихся подмножества В приведенной матрице исследуем все нулевые переходы.
Наибольшая сумма констант приведения равна υ36=1+1=2, следовательно, множество разбивается на два подмножества Оценка длины цикла: Оценка на перспективном множестве: В результате получим другую сокращенную матрицу (3x3), которая подлежит операции приведения.
После операции приведения сокращенная матрица будет иметь вид:
d3=0 Шаг №4. Определяем ребро ветвления и разобьем все множество допустимых значений Q3относительно этого ребра на два непересекающихся подмножества В приведенной матрице исследуем все нулевые переходы.
Наибольшая сумма констант приведения равна υ52=1+5=6, следовательно, множество разбивается на два подмножества Оценка длины цикла: Оценка на перспективном множестве: В результате получим другую сокращенную матрицу (2x2), которая подлежит операции приведения. После операции приведения сокращенная матрица будет иметь вид:
В соответствии с этой матрицей включаем в маршрут Ответ: l* =C15+C52+C24+C43+C36+C61=1+1+1+1+1+1=6. Дерево решения имеет следующий вид:
Задание №3. Оптимизация дискретных управлений дискретными динамическими объектами методом динамического программирования Р. Беллмана Дано:
U – н.у. (неограниченное управление), (4)
Найти: Решение 1. Минимизируем
Вычислим S3от x3:
2. Минимизируем
Вычислим S2от U2:
3. Минимизируем
Вычислим S1от U2:
4. Минимизируем
Вычислим S0от U0:
Рассчитаем оптимальный процесс:
Рассчитаем оптимальное программное управление:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 209. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (7)
, (7) , (8)
, (8)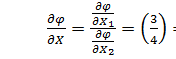 , (9)
, (9) , (10)
, (10)

 , находится на пересечении линий DFи EFи ее координаты определяются путем решения одноименных уравнений (1’) и (2’).
, находится на пересечении линий DFи EFи ее координаты определяются путем решения одноименных уравнений (1’) и (2’). ,
,  , (12)
, (12)
 ).
). ) и (
) и (  ), т.е.
), т.е. 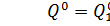 , где
, где 
 и
и  .
. .
. .
. и
и  .
. .
.
 .
. и
и 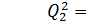 .
. .
.
 .
. и
и  .
. .
.
 и
и  .
.





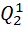




























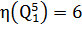
 (1) k=0,1,2,3
(1) k=0,1,2,3 (2)
(2)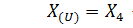 , (3) n=4
, (3) n=4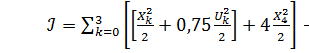 , (5)
, (5) (6).
(6).