
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Ряды с неотрицательными членамиРядом с неотрицательными членами называется ряд Для исследования на сходимость таких рядов используют признаки сходимости рядов с неотрицательными членами. 2.1. Признаки сходимости рядов с неотрицательными членами Признаки сравнения. Пусть даны два ряда с неотрицательными членами I. если выполняется неравенство Пример. Исследуем на сходимость ряд Аналогично можно показать, что любой ряд вида при II. Если существует предел отношения общих членов рядов Пример. Исследуем на сходимость ряд Сравним его с рядом III. Если выполняется неравенство Признак Коши. Пусть для ряда а) если б) если  в) если Пример. Исследуем сходимость ряда
Очевидно, что признак Коши целесообразно применять в случае, когда общий член ряда является Признак Даламбера. Пусть для ряда а) если б) если в) если Пример. Исследуем сходимость ряда Для заданного ряда Интегральный признак Коши. Пусть члены ряда Пример. Исследуем сходимость обобщённого гармонического ряда Функция
При Интегральный признак Коши целесообразно использовать в случае, когда общий член ряда интегрируем.
Знакочередующиеся ряды Определение 13.Ряд называется знакочередующимся, если он имеет бесконечное число как положительных, так и отрицательных членов, причём они в ряде чередуются:
Например, Справедлива следующая теорема: |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 208. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
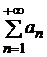 , где
, где  .
.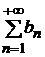 , где
, где  , тогда справедливы следующие признаки сравнения:
, тогда справедливы следующие признаки сравнения: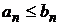 при всех
при всех  , то из сходимости большего ряда
, то из сходимости большего ряда  . Для всех
. Для всех  . Следовательно, из расходимости гармонического ряда следует расходимость исходного ряда.
. Следовательно, из расходимости гармонического ряда следует расходимость исходного ряда. (14)
(14) расходится. Ряд (14) называется обобщённым гармоническим рядом.
расходится. Ряд (14) называется обобщённым гармоническим рядом. ), не равный нулю и конечный, то ряды
), не равный нулю и конечный, то ряды  .
. , который сходится (см. пример на стр. 18). Предел отношения общих членов этих рядов равен
, который сходится (см. пример на стр. 18). Предел отношения общих членов этих рядов равен  . Следовательно, исходный ряд, так же как и ряд
. Следовательно, исходный ряд, так же как и ряд  при всех
при всех  существует предел
существует предел  , тогда
, тогда , ряд
, ряд  , ряд
, ряд  , теорема не даёт ответа на вопрос о сходимости, и нужно использовать другие признаки.
, теорема не даёт ответа на вопрос о сходимости, и нужно использовать другие признаки. .
.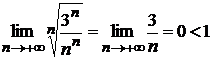 . Ряд сходится.
. Ряд сходится. -го члена к
-го члена к  , тогда
, тогда .
. ,
, 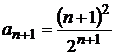 ,
, 
 и ряд сходится.
и ряд сходится.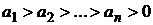 и
и  – непрерывная положительная убывающая функция, определённая при
– непрерывная положительная убывающая функция, определённая при  , такая, что
, такая, что  , …,
, …,  , тогда несобственный интеграл
, тогда несобственный интеграл  и ряд
и ряд 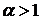 .
.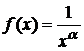 удовлетворяет условиям интегрального признака Коши. Рассмотрим несобственный интеграл
удовлетворяет условиям интегрального признака Коши. Рассмотрим несобственный интеграл
 .
. . Следовательно, обобщённый гармонический ряд
. Следовательно, обобщённый гармонический ряд  , сходится.
, сходится. (15)
(15) – знакочередующийся ряд.
– знакочередующийся ряд.