
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дифференциальные уравнения первого порядкаСтр 1 из 5Следующая ⇒ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Нижегородский государственный университет им. Н.И. Лобачевского Е.А. Голубева МАТЕМАТИЧЕСКИЙ АНАЛИЗ Часть II Учебно-методическое пособие Рекомендовано объединённой учебно-методической комиссией филиалов и ФПРК для студентов ННГУ, обучающихся по направлению подготовки 080100 «Экономика»
Нижний Новгород 2013 УДК 517 ББК 22.16 Г-62
Г-62 Голубева Е.А. МАТЕМАТИЧЕСКИЙ АНАЛИЗ. Часть II: Учебно-методическое пособие. – Нижний Новгород: Нижегородский госуниверситет, 2013. – 40 с.
Рецензент: к.т.н. В.А. Гришин
В учебно-методическом пособии в краткой форме излагается теоретический материал и даны примеры решения типовых задач по следующим разделам математического анализа: «Дифференциальные уравнения», «Ряды». Приведены вопросы для подготовки к экзамену и варианты контрольной работы. Пособие предназначено для студентов ННГУ, обучающихся по направлению подготовки 080100 «Экономика». Оно поможет сориентироваться при написании контрольной работы, подготовке к практическим занятиям, экзамену или зачёту.
Ответственный за выпуск: председатель объединённой учебно-методической комиссии филиалов и ФПРК к.т.н., доцент Д.Н. Шуваев
УДК 517 ББК 22.16
© Нижегородский государственный Университет им. Н.И. Лобачевского, 2013 СОДЕРЖАНИЕ ВВЕДЕНИЕ…………………………………………………………………....4
Тема 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ………………………......4
1. Дифференциальные уравнения первого порядка……..….……….......5  1.1. Дифференциальные уравнения с разделяющимися переменными………...…...…………………..6 1.2. Однородные дифференциальные уравнения первого порядка………………………..……………...……….…..8 1.3. Линейные дифференциальные уравнения первого порядка…..10 1.4. Дифференциальные уравнения Бернулли…………….………..12 1.5. Дифференциальные уравнения в полных дифференциалах…..14 2. Дифференциальные уравнения второго порядка……….…….…….16 2.1. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами….………...16
Тема 2. РЯДЫ……………………………………………...……………..….18
1. Понятие числового ряда…………..……………………....…………..18 1.1. Необходимое условие сходимости ряда……….………...……..19 1.2. Свойства сходящихся рядов….......…….………......…………...20 2. Ряды с неотрицательными членами…………...……………………..20 2.1. Признаки сходимости рядов с неотрицательными членами.....20 3. Знакочередующиеся ряды………………..………………..………….23 4. Знакопеременные ряды…………...…..……………………………….24 5. Степенные ряды…………………….…………………..……………..26 5.1. Свойства степенных рядов…………………….………………...27 5.2. Разложение функций в степенные ряды….…………..………...28 5.3. Применение рядов в приближённых вычислениях……………30
Приложение 1. ВОПРОСЫ ДЛЯ ЭКЗАМЕНА……………………..……..32
Приложение 2. ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ……………33
ЛИТЕРАТУРА…………………………………………………………….....39 ВВЕДЕНИЕ Дисциплины математического цикла служат фундаментальной базой экономического образования. Математический анализ является наиболее сложной из этих дисциплин. Настоящее пособие предназначено для помощи студентам, обучающимся по направлению подготовки 080100 «Экономика» как очной, так и заочной форм обучения. Оно является дополнением и продолжением учебно-методического пособия «Математический анализ. Часть I» того же автора. В основу структуры пособия положен тематический принцип. Сюда вошёл материал, относящийся к таким темам математического анализа, как «Дифференциальные уравнения» и «Ряды». Наряду с изложением основного теоретического материала по вышеперечисленным темам, в пособии приведены примеры решения типовых задач, вопросы для подготовки к экзамену и варианты контрольной работы. Тема 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Дифференциальными называются уравнения, содержащие неизвестную функцию и её производные. Они занимают важное место в высшей математике и имеют многочисленные приложения в разных науках.
Дифференциальные уравнения первого порядка Определение 1. Дифференциальным уравнением первого порядка называется уравнение, содержащее неизвестную функцию и её первую производную, то есть уравнение вида где Если уравнение (1) можно разрешить относительно и называется дифференциальным уравнением первого порядка, разрешённым относительно производной. Например, уравнения Определение 2.Решением дифференциального уравнения называется функция Например, функция Определение 3.Общим решением дифференциального уравнения называется функция Таким образом, функция В теории дифференциальных уравнений основным является вопрос о существовании и единственности решения. Ответ на него даёт теорема Коши. Теорема Коши: Пусть дано дифференциальное уравнение (2), разрешённое относительно производной. Если функция Условия, которые задают значение функции Задача нахождения решения дифференциального уравнения (2), удовлетворяющего условию (3), называется задачей Коши. Начальные условия (3) из множества интегральных кривых выделяют ту, которая проходит через точку
1.1. Дифференциальные уравнения с разделяющимися переменными Определение 4.Дифференциальное уравнение первого порядка вида где Алгоритм решенияуравнений вида (4) носит название «разделение переменных» и состоит в следующем: 1) Разделить переменные, то есть добиться, чтобы в левой части уравнения стояла только переменная
2) Если необходимо, перейти от производных к дифференциалам, учитывая, что
3) Вычислить интегралы от левой и правой частей:
4) Подстановкой в исходное уравнение проверить, являются ли решениями нули функций, на которые делили в пункте 1 (в данном случае нули функции Примеры. 1) Найдём общие решения дифференциальных уравнений: а) Перепишем уравнение в виде Интегрируя обе части, имеем Ответ: б) Разделим переменные, для чего перенесём
Интегрируя обе части, имеем При потенцировании получаем Проверим, является ли решением Ответ: Семейство интегральных кривых представляет собой пучок возрастающих экспонент, проходящих через точку в) Разделим переменные, перенеся
Интегрируя обе части, имеем Проверим, являются ли решениями Подставляя
Ответ: Семейство интегральных кривых представляет пучок прямых, проходящих через начало координат. 2) Найдём частное решение уравнения Разделяя переменные, найдём общее решение:
Подставляя координаты точки Ответ:
1.2. Однородные дифференциальные уравнения первого порядка Определение 5.Функция Например, Определение 6.Дифференциальное уравнение вида
где Это уравнение можно привести к виду
где С помощью замены
Примеры.Найдём общие решения дифференциальных уравнений. 1) Это уравнение является однородным, так как функции
или
Последнее уравнение является уравнением с разделяющимися переменными. Поделим обе его части на
Интегрируя левую и правую части, имеем
или
Сделав обратную замену Проверим, является ли Ответ: 2) Так как Сделаем замену
Сократив на
или
Последнее уравнение является дифференциальным уравнением с разделяющимися переменными. Разделив обе части уравнения на
Интегрируя левую и правую части, имеем
Сделав обратную замену
Проверим, являются ли решениями Ответ: 1.3. Линейные дифференциальные уравнения первого порядка Определение 7.Уравнение вида где Если Общее решение уравнения (5) можно найти двумя способами: I. По формуле Пример.Найдём общее решение уравнения В этом уравнении
II. Методом вариации произвольной постоянной. При решении линейных дифференциальных уравнений методом вариации произвольной постоянной сначала решают соответствующее однородное уравнение. Чтобы найти общее решение исходного неоднородного уравнения, в полученном решении произвольную постоянную считают функцией от Примеры.1) Решим уравнение Общее решение заданного неоднородного уравнения будем искать в том же виде, только произвольную постоянную считаем уже функцией от
Дифференцируя, имеем
Подставляя в исходное уравнение выражения для
или
откуда
Следовательно, общее решение заданного уравнения имеет вид Ответ: 2) Найдём общее решение уравнения Решаем соответствующее однородное уравнение:
Потенцируя, получаем
Заметим, что
Общее решение заданного неоднородного уравнения будем искать в том же виде, только произвольную постоянную считаем уже функцией от
Дифференцируя, имеем
Подставляя в исходное уравнение выражения для
откуда
Следовательно, общее решение заданного уравнения имеет вид
Ответ:
1.4. Дифференциальные уравнения Бернулли Определение 8.Уравнение вида где Данное уравнение приводится к линейному подстановкой Пример.Решим уравнение Данное уравнение является уравнением Бернулли, в котором
Положим
Решаем однородное уравнение
Разделяя переменные
и интегрируя, находим
После потенцирования получаем
В найденное решение можно включить частное решение
Общее решение уравнения
Дифференцируя, имеем
Подставляя в данное уравнение выражение для
Таким образом, общее решение линейного уравнения имеет вид
Выполняя обратную замену, получаем, что общим решением исходного уравнения является функция
Заметим, что Ответ:
1.5. Дифференциальные уравнения в полных дифференциалах Определение 9.Уравнение вида где левая часть представляет собой полный дифференциал некоторой функции Критерием того, что уравнение (8) есть дифференциальное уравнение в полных дифференциалах является выполнение равенства
Действительно, так как левая часть представляет собой полный дифференциал некоторой функции Решение дифференциального уравнения (8) сводится к отысканию функции Примеры.Найдём общие решения следующих дифференциальных уравнений: 1) В этом уравнении
Интегрируя левую и правую части по Чтобы найти
Подставляя найденное
Общее решение исходного уравнения принимает вид
Полагая
Ответ: 2) В этом уравнении Интегрируя левую и правую части последнего равенства по Чтобы найти
Подставляя найденное
Общее решение исходного уравнения принимает вид
Полагая
Ответ:
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 182. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (1)
, (1) – независимая переменная,
– независимая переменная,  – искомая функция,
– искомая функция, 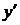 – её производная.
– её производная. (2)
(2) ,
,  ,
,  являются дифференциальными уравнениями первого порядка, разрешёнными относительно производной.
являются дифференциальными уравнениями первого порядка, разрешёнными относительно производной. , определённая на некотором интервале
, определённая на некотором интервале 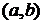 , которая при подстановке в уравнение обращает его в тождество. График решения дифференциального уравнения называется интегральной кривой.
, которая при подстановке в уравнение обращает его в тождество. График решения дифференциального уравнения называется интегральной кривой. тождественно обращает в ноль левую часть уравнения
тождественно обращает в ноль левую часть уравнения 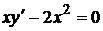 и поэтому представляет собой решение этого уравнения. Аналогично, функции
и поэтому представляет собой решение этого уравнения. Аналогично, функции  ,
, 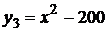 и, вообще, любая функция вида
и, вообще, любая функция вида  , где
, где  – любое действительное число, является решением дифференциального уравнения
– любое действительное число, является решением дифференциального уравнения  , удовлетворяющая этому уравнению при произвольном значении постоянной
, удовлетворяющая этому уравнению при произвольном значении постоянной  . На плоскости
. На плоскости  общее решение представляет собой семейство интегральных кривых.
общее решение представляет собой семейство интегральных кривых. и её производная
и её производная 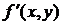 непрерывны в некоторой области
непрерывны в некоторой области  плоскости
плоскости  этой области существует единственное решение уравнения (2), удовлетворяющее условию
этой области существует единственное решение уравнения (2), удовлетворяющее условию 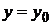 при
при  .
. в фиксированной точке
в фиксированной точке  , называют начальными условиями (условиями Коши) и записывают в форме:
, называют начальными условиями (условиями Коши) и записывают в форме: . (3)
. (3) , (4)
, (4)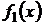 и
и 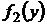 – непрерывные функции, называется дифференциальным уравнением с разделяющимися переменными.
– непрерывные функции, называется дифференциальным уравнением с разделяющимися переменными. ,
,  .
. :
: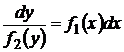 .
. .
. .
. .
. , где
, где  – произвольная постоянная. Выражая искомую функцию
– произвольная постоянная. Выражая искомую функцию  ,
, 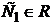 , что эквивалентно уравнению
, что эквивалентно уравнению  ,
,  .
. .
. .
. и умножим их на
и умножим их на  . Получим
. Получим ,
, 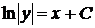 , где
, где  ,
,  , что эквивалентно уравнению
, что эквивалентно уравнению  ,
,  .
.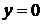 . Подстановка в исходное уравнение приводит к тождеству:
. Подстановка в исходное уравнение приводит к тождеству:  . Следовательно,
. Следовательно,  .
. .
. и умножив их на
и умножив их на  ,
,  , где
, где  или
или 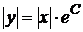 ,
, 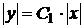 ,
,  ,
,  и
и  . Это не тождество, следовательно,
. Это не тождество, следовательно,  , проходящее через точку
, проходящее через точку  ,
,  ,
,  .
. . Тогда частное решение имеет вид
. Тогда частное решение имеет вид  .
. называется однородной функцией порядка
называется однородной функцией порядка  , если для любого числа
, если для любого числа  выполняется равенство
выполняется равенство  .
. – однородная функциявторого порядка, так как
– однородная функциявторого порядка, так как  ;
;  – однородная функция первого порядка;
– однородная функция первого порядка; 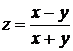 – однородная функция нулевого порядка.
– однородная функция нулевого порядка. ,
, ,
,  – однородные функции одного порядка, называется однородным дифференциальным уравнением первого порядка.
– однородные функции одного порядка, называется однородным дифференциальным уравнением первого порядка.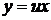 , где
, где  – новая неизвестная функция,
– новая неизвестная функция,  или
или  , однородное дифференциальное уравнение сводится к уравнению с разделяющимися переменными.
, однородное дифференциальное уравнение сводится к уравнению с разделяющимися переменными. .
. ,
,  обе являются однородными функциями первого порядка. Сделаем замену
обе являются однородными функциями первого порядка. Сделаем замену 
 ,
,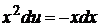 .
. , получим
, получим ,
,  .
.
 , где
, где  ,
,  , получим
, получим  ,
, 
 .
. – однородная функция нулевого порядка, то данное уравнение также является однородным.
– однородная функция нулевого порядка, то данное уравнение также является однородным.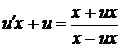 .
.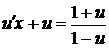
 ,
, ,
, .
. и умножив на
и умножив на  .
.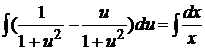 ,
, .
. ,
,  или
или  . Подставляя
. Подставляя  , (5)
, (5) и
и 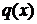 – непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
– непрерывные функции, называется линейным дифференциальным уравнением первого порядка. , то уравнение (5) называется линейным однородным дифференциальным уравнением первого порядка, в противном случае – линейным неоднородным.
, то уравнение (5) называется линейным однородным дифференциальным уравнением первого порядка, в противном случае – линейным неоднородным.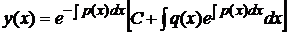 . (6)
. (6) .
. ,
,  – непрерывные функции, поэтому последнее уравнение является линейным. Найдём решение уравнения по формуле (6):
– непрерывные функции, поэтому последнее уравнение является линейным. Найдём решение уравнения по формуле (6): , где
, где  вторым способом. Решением соответствующего однородного уравнения
вторым способом. Решением соответствующего однородного уравнения  .
. .
.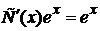 ,
,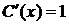
 ,
, .
.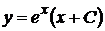 .
.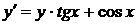 .
.
 ,
,  ,
, ,
,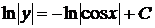 .
. ,
,  .
. .
. .
. ,
, ,
, ,
, .
. .
. , (7)
, (7) . Можно также применять подстановку
. Можно также применять подстановку 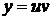 или метод вариации произвольной постоянной.
или метод вариации произвольной постоянной.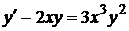 .
. ,
,  ,
, 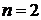 . Разделим обе части уравнения на
. Разделим обе части уравнения на  , получим
, получим ,
,  , тогда
, тогда  . Умножая обе части последнего уравнения на (-1) и выполняя указанную подстановку, имеем линейное дифференциальное уравнение первого порядка
. Умножая обе части последнего уравнения на (-1) и выполняя указанную подстановку, имеем линейное дифференциальное уравнение первого порядка .
.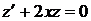 .
.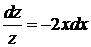 ,
, 
 .
.
 , имеем
, имеем ,
,  .
. .
. и
и  , получаем
, получаем ,
, ,
, .
. .
. .
.
 в области
в области  , называется дифференциальным уравнением в полных дифференциалах.
, называется дифференциальным уравнением в полных дифференциалах. .
. , где
, где 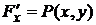 ,
,  , то
, то  ,
,  , а для непрерывной функции смешанные частные производные второго порядка равны между собой.
, а для непрерывной функции смешанные частные производные второго порядка равны между собой. .
. .
. ,
,  ,
, 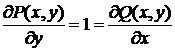 . Следовательно, исходное уравнение является уравнением в полных дифференциалах, и выражение
. Следовательно, исходное уравнение является уравнением в полных дифференциалах, и выражение  представляет собой полный дифференциал некоторой функции
представляет собой полный дифференциал некоторой функции  ,
,  , то есть
, то есть .
.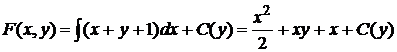 . (9)
. (9) используем тот факт, что
используем тот факт, что  ,
, ,
, ,
, .
.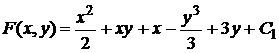 .
. .
. , получаем окончательное решение исходного уравнения:
, получаем окончательное решение исходного уравнения: .
. .
.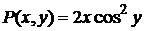 ,
,  ,
,  . Следовательно, исходное уравнение – дифференциальное уравнение в полных дифференциалах, и выражение
. Следовательно, исходное уравнение – дифференциальное уравнение в полных дифференциалах, и выражение  является полным дифференциалом некоторой функции
является полным дифференциалом некоторой функции  ,
,  , то есть
, то есть  .
. . (10)
. (10) ,
, ,
, ,
, ,
, .
. .
.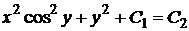 .
. , получаем окончательное решение исходного уравнения:
, получаем окончательное решение исходного уравнения: .
.