Студопедия
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
|
Пример программы разветвленной структуры
Задача.
1. Вычислить значение функции:
y= 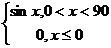
Значение аргумента х в градусах ввести с клавиатуры.
2. Таблица идентификаторов
| №
| Наименование переменной
| Обозначения в программе
| | 1
| Функция
| y
| | 2
| Аргумент
| x
|
3. Листинг программы.
program lab2;
uses
crt;
var
x, y: real;
begin
clrscr;
writeln (’Введите x’);
readln (x);
if x>90 then writeln(’функция не определена’)
else
{составной оператор}
begin
if x<0 then y: = 0
else y: = sin (x*pi/180);
writeln (’y = ’,y:8:3);
end;
readln;
end.
Вопросы для самоконтроля
- Какие алгоритмические конструкции называются ветвлениями?
- Для чего используют оператор goto?
- Почему при использовании нескольких условий в одном операторе if … then … else, каждое условие заключается в круглые скобки?
- Перечислите основные логические операции.
- Перечислите основные операции отношения.
- В каких случаях прибегают к использованию оператора case … of ?
Методические указания для выполнения практического задания №5. «Ветвления»
Цель работы: Ознакомиться с алгоритмами разветвленной структуры, логическим оператором, оператором выбора.
Задание:
1. В приложении 6 выбрать свой вариант задания.
2. Выполнить практическое задание №5, используя пример программы разветвленной структуры.
3. Составить блок-схему алгоритма.
4. Написать программу и отладить ее по заранее подготовленному тесту.
5. Оформить задание в тетради для практических занятий.
6. Результат выполнения программы предъявить преподавателю.
7. Ответить на вопросы самоконтроля.
8. Защитить выполненную работу у преподавателя.
Приложение 6. Таблица вариантов заданий
| Вариант
| Задание
| | 1
| Переменной k присвоить номер четверти плоскости, в которой находится точка с координатами x и y (xy=0).
| | 2
| Если сумма трех попарно различных действительных чисел x, y, z меньше единицы, то заменить меньшее из x и y полусуммой двух других, в противном случае уменьшить все числа в 5 раз.
| | 3
| Даны три действительных числа. Выбрать из них те, которые принадлежат интервалу (1, 3).
| | 4
| Написать программу, которая выбирает наименьшее из четырех заданных чисел.
| |
| Даны три действительных числа. Возвести в квадрат те из них, значения которых неотрицательны.
| | 6
| Даны действительные числа х, у, и z. Вычислить max (x + y + z, xyz).
| | 7
| Поменять местами значения переменных a, b, c не равных между собой таким образом, чтобы а > b > c.
| | 8
| Меньшее из двух значений переменных вещественного типа заменить нулем, а в случае их равенства – заменить нулями оба.
| | 9
| Если сумма трех попарно различных действительных чисел x, y, z меньше единицы, то наименьшее из этих трех чисел заменить полусуммой двух других, в противном случае возвести все числа в квадрат.
| | 10
| Наибольшее из трех различных значений переменных целого типа х, у и z уменьшить на 3.
| | 11
| Даны два действительных числа, не равных между собой. Меньшее из них заменить их полусуммой.
| | 12
| Если значение w не равно 0 и при этом котангенс от w меньше 0.5, тогда поменять знак у w, а если значение равно 0, тогда присвоить w значение 1.
| | 13
| Даны действительные числа х, у и z. Получить min (x,y,z).
| | 14
| Две точки плоскости заданы своими координатами. Определить, лежат ли они в одной или разных координатных плоскостях.
| | 15
| Даны действительные числа х, у, и z. Вычислить min( (x + y + z / 2), (x*y*z) ) +1.
| | 16
| Даны действительные числа a, b, c. Удвоить эти числа, если a > b > c, и заменить их абсолютными значениями, если это не так.
| | 17
| Известно, что из четырех чисел одно отлично от трех других, равных между собой. Присвоить номер этого числа переменной n.
| | 18
| Написать программу, которая выбирает наибольшее из четырех заданных чисел.
| | 19
| Даны действительные числа x и y. если x и y отрицательны, то каждое значение заменить его модулем; если отрицательно только одно из них, то оба значения увеличить на 0.5, в противном случае извлечь из каждого квадратный корень.
| | 20
| Две точки плоскости заданы своими координатами. Определить, лежат ли они в одной (распечатать ее номер) или разных координатных четвертях.
| | 21
| Даны два действительных числа. Заменить первое число нулем, если оно меньше или равно второму, и удвоить оба числа в противном случае.
| | 22
| Даны действительные числа a, b, c, d. Если a < b < c < d, то каждое число заменить небольшим из них; если a > b > c > d, то числа оставить без изменения; в противном случае все числа заменить их квадратами.
| | 23
| Даны действительные числа х, у и z. Получить max (x,y,z).
| | 24
| Даны три действительных числа. Выбрать из них те, которые принадлежат интервалу (1, 3).
| | 25
| Меньшее из двух значений переменных вещественного типа заменить нулем, а в случае их равенства – заменить нулями оба.
| | 26
| Даны действительные числа х, у и z. Обнулить отрицательные числа.
| | 27
| Известно, что из трех целых чисел одно отлично от трех других, равных между собой. Присвоить номер этого числа переменной n.
| | 28
| Наименьшее из трех различных значений переменных целого типа х, у и z увеличить на 3.
| | 29
| Если сумма трех попарно различных действительных чисел x, y, z больше единицы, то наибольшее из этих трех чисел заменить полусуммой двух других, в противном случае возвести все числа в квадрат.
| | 30
| Даны два действительных числа, не равных между собой. Наибольшее из них заменить их полусуммой.
|
Циклические вычислительные процессы
|