
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Двойственная задача линейного программирования ⇐ ПредыдущаяСтр 2 из 2 1.4.1 Пример прямой и двойственной задачи линейного программирования
Обратимся к задаче рационального использования ресурсов. Пусть для осуществления l технологических процессов T1,…,Tl предприятию требуется m ресурсов S1,…, Sm. Запасы ресурсов каждого вида ограничены и равны b1,…,bm. Известен расход ресурсов {aij}, i= xj и ее решение может быть найдено симплекс-методом. Зададимся вопросом, какова с точки зрения предприятия ценность имеющихся в его распоряжении ресурсов. При решении этого вопроса будем иметь в виду, что ресурсы, которые предприятие не может полностью использовать, имеют для него очень низкую ценность, в том смысле, что предприятие не будет нести даже небольшие расходы на увеличение запасов этих ресурсов. Заметим при этом, что рыночная цена этих ресурсов может быть большой (скажем дорогостоящее неиспользуемое или используемое не на полную мощность оборудование). Наибольшую ценность будут иметь те ресурсы, которые в наибольшей степени ограничивают выпуск продукции, а следовательно и доход предприятия. Итак, можно считать, что каждый вид ресурса обладает некоторой, говорят, «теневой ценой», определяющей ценность данного ресурса для предприятия с точки зрения дохода от реализации выпускаемой продукции и зависящей от наличного запаса этого ресурса и потребности в нем для выпуска продукции.  Ясно, что варьируя план выпуска продукции, мы тем самым варьируем теневые цены используемых ресурсов, а потому ставится задача нахождения оптимальных теневых цен, которые соответствуют максимальному доходу предприятия, то есть оптимальному распределению ресурсов. Оптимальные теневые цены называют объективно обусловленными или оптимальными оценками. Построим математическую модель для определения оптимальных теневых цен. Обозначим через yi теневую цену ресурса Si . Величины yi должны быть такими, чтобы теневая цена ресурсов, используемых в любом технологическом процессе, на производство единицы продукции не была меньше получаемого дохода от единицы продукции. Оптимальными теневыми ценами естественно считать такие, которые минимизируют общую теневую стоимость ресурсов, то есть величину g*= Задача нахождения минимума целевой функции (1.40) при условиях (1.39) представляет собой задачу линейного программирования и называется двойственной по отношению к задаче (1.37)–(1.38).
1.4.2 Общая формулировка прямой и двойственной задачи
Дадим достаточно общее определение двойственной задачи по отношению к прямой, заданной в виде:
f = c1x1 + c2x2 + …+ cnxn при условиях
a21x1 + a22 x2 +…+ a2n xn < R2 > b2 . . . . . . . . . . . . . (1.42) am1 x1 + am2 x2 +…+ amn xn < Rm > bm x1 где: R1,R2, …, Rn – операция отношения вида либо =, либо ≤ одновременно. Очевидно, что любую задачу линейного программирования можно представить в одной из двух указанных форм. Тогда двойственной по отношению к задаче (1.41)−(1.42) будем называть задачу:
f *=b1y1+b2y2+…+bmym
при условиях
a12y1 + a22y2 +…+ am2ym …………………………… (1.44) a1ny1 + a2ny2 +…+ amnym и, если в прямой задаче Ri y1 Сформулируем правила построения двойственной задачи: а) целевая функция исходной задачи (1.41)−(1.42) задается на максимум, а целевая функция двойственной задачи (1.43)−(1.45) – на минимум; б) матрица системы сильных ограничений двойственной задачи получится из матрицы системы ограничений прямой задачи транспонированием; в) число переменных двойственной задачи равно числу сильных ограничений прямой, а число ограничений в двойственной задаче равно числу переменных прямой; г) коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены системы сильных ограничений прямой задачи, а правыми частями системы сильных ограничений двойственной задачи – коэффициенты при неизвестных в целевой функции исходной задачи. Отметим, что если все Ri≡(
1.4.3 Свойства двойственной задачи
Приведем теоремы, устанавливающие зависимости между решениями прямой и двойственной задач. ТЕОРЕМА 1.2. Значение целевой функции задачи (1.41)–(1.42) при любом допустимом плане x не превышает значения целевой функции задачи (1.43)–(1.45) при любом ее допустимом плане y: f( Если для каких-нибудь x и узначения целевых функций совпадают, т.е. f( Доказательство. Пусть x=(x1,x2,…,xn) – допустимое решение задачи (1.41)–(1.42), у=(y1,y2,….,ym) – допустимое решение задачи (1.43)–(1.45). Подставим решение x в ограничения (1.42), умножим первое равенство на y1, второе на y2,…, m–е на ym и сложим полученные равенства:
Перегруппируем слагаемые в левой части:
Так как y – допустимое решение задачи (1.43)–(1.45), то для любого j (j=1,2,…,n) , имеем:
Заменяя в (1.46) суммы, заключенные в скобки, соответствующими cj и учитывая, что xj ≥ 0 , получаем:
или, что тоже самое f(x)≤f *(y). Первая часть теоремы доказана. Пусть для каких-нибудь x,y имеем: (c,x′)>(bT,y). Допустим от противного, что x не является оптимальным решением задачи (1.41)–(1.42). Это значит, что есть такое другое допустимое решение x′задачи (1.41)–(1.42), что (c,x′) > (c,x) = (bT,y), а это противоречит первой части данной теоремы. Следовательно, при нашем условии x– оптимальное решение задачи (1.41)–(1.42). Аналогично показывается, что y - оптимальное решение задачи (1.43)–(1.45).Теорема доказана.
ТЕОРЕМА 1.3. Если одна из пар двойственных задач (1.41)–(1.42) или (1.43)–(1.45) имеет оптимальное решение, то и другая также имеет оптимальное решение, причем их оптимумы совпадают (max f=min f *). Если целевая функция одной из пары двойственных задач не ограничена (для прямой – сверху, а для двойственной − снизу), то допустимая область другой задачи пуста. Доказательство. Ввиду взаимной двойственности задач (1.41)–(1.42) и (1.43)–(1.45) достаточно провести доказательство, принимая за исходную одну из задач. Пусть, например, задача (1.41)–(1.42) имеет оптимальные решения, и
При рассмотрении симплекс-метода мы выяснили, что вектор
где Введем обозначение:
Тогда неравенство (1.48) принимает вид
Оно означает, что вектор Докажем, что y– оптимальное решение задачи (1.43) – (1.45). Имеем:
Таким образом, значение целевой функции задачи (1.43) –(1.45) при её допустимом решении y совпадает с значением целевой функции задачи (1.41)–(1.42) при её допустимом решении Докажем вторую её часть. Пусть известно, что целевая функция, например, задачи (1.41)–(1.42) не ограничена сверху на допустимом множестве. Допустим, от противного, что задача (1.43)–(1.45) имеет при этом допустимое решение, и пусть y – одно из них. Ввиду неограниченности целевой функции задачи (1.41)–(1.42) найдётся такое допустимое её решение x, для которого значение целевой функции будет больше числа (b,y):
что противоречит теореме 1.2. Теорема доказана. При доказательстве первой части теоремы мы установили следующее: если B – базисная матрица оптимального опорного решения канонической задачи (1.41)–(1.42), то
– оптимальное решение двойственной к (1.41)–(1.42) задачи (1.43)-(1.45). Этим фактом мы будем пользоваться в дальнейшем.
Рассмотрим, в качестве примера, следующую задачу и двойственную к ней.
f =5x1+10x2
5x1 + 8x2 x1 + 4x2 x1
Оптимальное решение прямой задачи, приведенное в последней симплекс таблице: xT=(16,8,8,0,0) получено в базисе
B = 0 5 8 ; 0 1 4 0 –1 5
y* = cB max f = f (x*) = 160 = min f *(y*).
В том случае, когда среди векторов (
yk=αjk+cjk, k = y*=(y1,…, ym)T,
где αjk – элементы строки оценок в последней симплекс-таблице решения прямой задачи, а cjk – соответствующие коэффициенты целевой функции прямой задачи. Рассмотрев предыдущий пример, можем убедиться, что поскольку в исходной задаче векторы
y2 = α4 + c4 = 5/6 + 0 = 5/6 y3 = α5 + c5 = 5/6 + 0 = 5/6 . y*= (0; 5/6; 5/6).
1.4.4 Анализ чувствительности
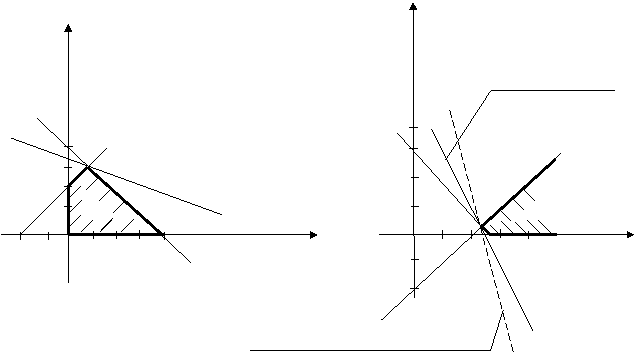
Нас будет интересовать вопрос: какое воздействие окажут изменения, вносимые в те или иные параметры задачи линейного программирования, на ее решение, на решение двойственной задачи, на оптимальные значения целевой функции ? А именно, изучим: а) воздействие дополнительного количества дефицитного ресурса; б) воздействие дополнительного количества недефицитного ресурса; в) воздействие изменений в коэффициентах целевой функции. Для наглядности исследований рассмотрим прямую и двойственную задачи линейного программирования и их геометрическое решение (рисунок 1.5). Пример 1.5.
f = 2x1 + 3x2
–x1 + x2 x1 x2 y2
f *= 4y1 + 2 y2 =c0 =11
M(1,3) f = 2x1 + 3x2 = 11 M(2.5;0.5)
x1 y1
f * = (4 +∆b1) y1 + (2 + ∆b2) y2 = c1
Рисунок 1.5 - Решение задачи линейного программирования геометрическим способом.
Приведем заключительную симплекс-таблицу решения прямой задачи.
Таблица 1.6 – Заключительная симплекс-таблица
Очевидно, что значение целевой функции задачи линейного программирования f = f (b1, b2 ,…, bm) зависит, вообще говоря, от запасов ресурсов. Изменение ресурсов bi на малую величину ∆bi, i = 1,2,...,m ведет к изменению значения max f =min f *, но изменение min f *происходит, при малых ∆bi, не за счет изменения точки, в которой достигается min f * (допустимая область двойственной задачи вообще не изменится при изменении bi), а за счет изменения наклона поверхности (линии) уровня целевой функции f *, коэффициенты которой зависят от bi+∆bi. Следует отметить, что при больших изменениях bi, i= Рассмотрим влияние на устойчивость двойственных оценок приращений ∆bi дефицитных и недефицитных ресурсов. Очевидно, что увеличение недефицитных ресурсов не приведет к увеличению прибыли, а появление дополнительного количества дефицитных ресурсов улучшает, вообще говоря, оптимальное значение целевой функции. Однако необходимо принять во внимание, что изменение оптимального решения за счет увеличения количества дефицитных ресурсов приведет к улучшению значения целевой функции (прямой задачи) только в том случае, если сумма дополнительных издержек по обеспечению дополнительным количеством ресурса не превышает сумму прибыли, полученной в результате его использования. В рассмотренном примере увеличение ∆b2 на величину большую 2, то есть b2+∆b2>4, при фиксированном b1=4, перемещает оптимальное решение двойственной задачи в точку y1=3, y2=0 и min f *= max f =12. Таким образом, увеличение на 1 единицу произошло за счет увеличения ресурса b2 на величину ≥2. Причем, начиная со значения b2=4, этот ресурс перестает быть дефицитным. При 0<∆b2<2 и ∆b1>0 точка минимума f * не меняется, а значение целевой функции f * увеличивается, а следовательно, увеличивается и значение целевой функции прямой задачи. Это и есть область устойчивости двойственных оценок дефицитных ресурсов. Здесь же отметим, что если b1=4, b2>4, то уменьшая недефицитный ресурс b2 на величину ∆b2<0, мы при b2+∆b2<4 добьемся того, что оптимальное решение двойственной задачи будет достигаться в точке (2,5; 0,5) и ресурс y2 станет дефицитным, но значение min f *= max f уменьшится. В общем случае рассмотрим иной подход к изучению влияния ∆bi на область устойчивости двойственных оценок. Пусть B– матрица векторов исходной задачи, составляющих базис, в котором решение прямой задачи оптимально. Тогда последняя симплекс-таблица 1.7 формально может быть получена так:
Таблица 1.7 – Итоговая симплекс-таблица
Очевидно, что изменения запасов ресурсов на величины ∆bi не окажет влияния ни на разложения векторов
Оптимальное опорное решение (значения базисных переменных):
Пусть мы внесли изменения в вектор правых частей (увеличили запасы ресурсов)
тогда оптимальное опорное решение новой задачи (значения базисных переменных):
при условиях:
3 + (1/2)∆b1 + (1/2)∆b2 ∆b1
Область устойчивости двойственных оценок в этом случае нетрудно изобразить геометрически (рисунок 1.6).
Рисунок 1.6 – Область устойчивости Итак, область устойчивости: ∆b1 – любое неотрицательное и ∆b2 может принимать значения 0 В задачах большей размерности мы сможем, вообще говоря, лишь проверять попадают ли компоненты вектора Обратимся к вопросу влияния вариации коэффициентов целевой функции (c1,…,cn) прямой задачи на оптимальное решение. В частности нас интересует вопрос устойчивости решения прямой задачи относительно вариации коэффициентов целевой функции. Легко видеть, что вариация c1,…,cn не оказывает влияния на допустимую область задачи линейного программирования и нас интересует область изменения ∆c1, ∆c2,…, ∆cn , в которой точка достижения оптимального решения не изменится. Очевидно, что если рассматривать в качестве прямой задачи двойственную, то решение проблемы будет аналогично рассмотренному выше (роль b1,…,bm будут играть c1,…, cn). Например, в рассмотренном примере базисом оптимального решения двойственной задачи будут естественно векторы A1=(1,1)T и A2=(−1,1)T. Оптимальное опорное решение (значение базисных переменных)
Для изучения устойчивости внесем изменения в вектор цен с + ∆c = (2 + 3∆c1 + ∆c2). Найдем оптимальное опорное решение новой двойственной задачи (значение базисных переменных).
Потребуем: 5/2 + (1/2)∆c1 + (1/2)∆c2 1/2 − (1/2)∆c1 + (1/2)∆c2 ∆c1
что определяет область устойчивости решения прямой задачи относительно вариации коэффициентов (см. рисунок 1.7).
Область устойчивости
-5 -1 1 ∆c1
-5
Рисунок 1.7 − Область устойчивости
1.4.5 Экономическая интерпретация двойственных задач
Экономическую интерпретацию двойственных задач и двойственных оценок рассмотрим на примере. Для производства продукции двух видов А и В используются ресурсы трех видов I,II,III. Запасы ресурсов – bi, затраты ресурсов aij на производство единицы продукции каждого вида и цена cj единицы продукции приведены в таблице 1.8.
Таблица 1.8 – Таблица выпускаемой продукции
Требуется так спланировать производство, чтобы прибыль от реализации продукции была максимальной. Оценить теневые цены ресурсов и произвести анализ решения двойственной задачи. Обозначим
f = 2x1 + x2
2x1 + 4x2 x1 x1 x3
Решение прямой и двойственной задач приведено в заключительной симплекс-таблице 1.9.
Таблица 1.9 – Симплекс-таблица
Оптимальный план производства продукции вида А: x1=8; вида В: x2=2; fmax=18. Ресурсы типа I и III имеют теневые цены, большие нуля, поэтому дефицитны и в оптимальном плане используются полностью, что легко проверить по 1-му и 3-му ограничениям прямой задачи. Ресурс II типа имеет теневую цену равную нулю, является недефицитным и в оптимальном плане недоиспользуется в объеме 6 ед., что легко вычисляется из 2-го ограничения прямой задачи. Увеличение запасов дефицитного ресурса I типа ведет к увеличению прибыли от дополнительно произведенной продукции на одну единицу за счет следующих изменений в плане выпуска продукции: выпуск продукции вида В увеличивается на одну единицу, выпуск продукции вида А остается на прежнем уровне, а использование ресурса II типа увеличивается на 4 единицы (результаты получены из компонент столбца A3 и легко проверяются непосредственной проверкой). По аналогии при увеличении запасов дефицитного ресурса III типа на одну единицу прибыль от реализации дополнительно произведенной по новому оптимальному плану продукции также возрастает на одну единицу, при этом, как видно из последнего столбца симплекс – таблицы 1.9 необходимо увеличить выпуск продукции вида А на одну единицу и одновременно выпуск продукции вида В сократить на одну единицу. Использование ресурса II типа уменьшится еще на 2 единицы.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 202. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , j=
, j=  на единицу продукции по каждому технологическому процессу и стоимость единицы продукции каждого типа cj, j=
на единицу продукции по каждому технологическому процессу и стоимость единицы продукции каждого типа cj, j=  ; (1.37)
; (1.37) ; (1.38)
; (1.38)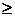 0, j =
0, j = 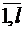
 . (1.39)
. (1.39) bi yi
bi yi  min. (1.40)
min. (1.40) a11 x1 + a12 x2 +…+ a1n xn < R1 > b1
a11 x1 + a12 x2 +…+ a1n xn < R1 > b1  a11y1 + a21y2 +…+ am1ym
a11y1 + a21y2 +…+ am1ym  (
( 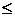 ), i=
), i=  , то
, то )
) 


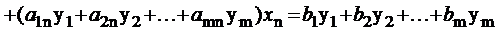 . (1.46)
. (1.46)
 ,
, – одно из них, найденное симплекс-методом, и
– одно из них, найденное симплекс-методом, и  – его базис. Тогда на последней итерации имеем
– его базис. Тогда на последней итерации имеем 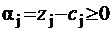 (j=1,2,…,n) так что zj ≥ cj, j=1,2,…,n, или, в векторной форме
(j=1,2,…,n) так что zj ≥ cj, j=1,2,…,n, или, в векторной форме . (1.47)
. (1.47) может быть найден по формуле
может быть найден по формуле
 ,
, – матрица, обратная к базисной матрице
– матрица, обратная к базисной матрице 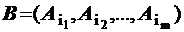 , A –матрица системы ограничений-уравнений задачи (1.42):
, A –матрица системы ограничений-уравнений задачи (1.42):  .Следовательно, из (1.47) имеем:
.Следовательно, из (1.47) имеем:
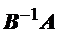
 (1.48)
(1.48)
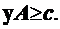
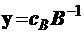 является допустимым решением задачи (1.43)-(1.45).
является допустимым решением задачи (1.43)-(1.45).

 .
. . Согласно теореме 1.2 это означает, что y оптимальное решение задачи (1.43)–(1.45). Первая часть теоремы доказана.
. Согласно теореме 1.2 это означает, что y оптимальное решение задачи (1.43)–(1.45). Первая часть теоремы доказана. ,
,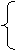
 4x1 + 3x2
4x1 + 3x2  3,
3,  1 4 3 12 –13 17
1 4 3 12 –13 17  ,
,  ,…,
,…,  ), решение двойственной задачи может быть найдено проще, а именно, компоненты вектора
), решение двойственной задачи может быть найдено проще, а именно, компоненты вектора ;
; y1 = α3 + c3 = 0 + 0 = 0
y1 = α3 + c3 = 0 + 0 = 0


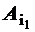 …
…

 ...
...

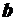 +∆
+∆  ,
,  ,
,  .
. .
. ,
,
 1 + (1/2)∆b1 –(1/2)∆b2
1 + (1/2)∆b1 –(1/2)∆b2 
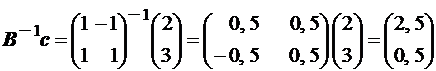 .
.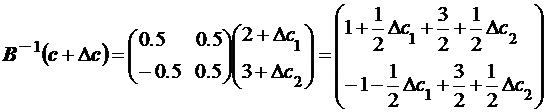 .
. ∆c2
∆c2  план выпуска продукции А, В, С, yi – теневые цены ресурсов I,II,III типа. Тогда прямая и двойственная задачи имеют вид:
план выпуска продукции А, В, С, yi – теневые цены ресурсов I,II,III типа. Тогда прямая и двойственная задачи имеют вид:
 x1 + x2
x1 + x2