
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Геометрическая интерпретация двумерной задачи линейного программирования и ее решениеСтр 1 из 2Следующая ⇒ Линейное программирование Примеры задач линейного программирования 1.1.1 Задача планирования выпуска продукции (планирование производства)
Машиностроительное предприятие для изготовления четырех видов продукции использует токарное, фрезерное, сверлильное, расточное и шлифовальное оборудование, а также комплектующие изделия. Кроме того, сборка изделий требует выполнения сборочно-наладочных работ. Нормы затрат всех видов ресурсов на изготовление каждого из изделий приведены в таблице (см. табл. 1.1). В этой же таблице указан имеющийся фонд каждого из ресурсов и прибыль от реализации одного изделия каждого вида.
Таблица 1.1−Нормы затрат на изготовление одного изделия
Продолжение таблицы 1.1
Надо составить такой план выпуска продукции, чтобы получить максимальную прибыль. Построим математическую модель данной задачи. Пусть x1 – планируемое количество изделий 1-го типа, x2, x3, x4 – планируемое количество изделий 2-го, 3-го, 4-го типов соответственно.  Тогда f=315x1+278x2+573x3+370x4 (1.1) прибыль предприятия. Так как нам надо получить как можно большую прибыль, то будем искать наибольшее (максимальное) значение функции f. Общие объемы ресурсов накладывают на нашу задачу ограничения
550x1 + 620x2 £ 64270 40x1 + 30x2+ 20x3 + 20x4 £ 4800 86x1 + 110x2 +150x3 + 52x4 £ 22360 160x1+ 92x2 + 158x3 + 128x4 £ 26240 (1.2) 158x2 + 30x3 + 50x4 £ 7900 3x1 + 4x2 + 3x3 + 3x4 £ 520 4.5x1 + 4.5x2 + 4.5x3 + 4.5x4 £ 720. Так как целевая функция и ограничения являются линейными, то это задача линейного программирования.
1.1.2 Задача планирования капитальных вложений
Для электроснабжения трех стройплощадок используются две трансформаторные подстанции. Первая стройплощадка потребляет 130 кВт, а вторая и третья по 140 кВт. Мощность первой ТП – 250 кВт, а второй 160 кВт. Расстояние от первой ТП – 600, 400, 200 м, до первой, второй и третьей площадки соответственно. От второй ТП: − 500, 300 и 200 м соответственно. Требуется составить схему электроснабжения с минимальными капитальными вложениями. Капитальные вложения для устройства линий рассчитываются по следующей формуле: где: Sij – мощность, потребляемая j-ой площадкой от i-ой ТП, кВт; lij – расстояние от j-ой площадки до i-ой ТП, м.; α – постоянный множитель. Итак, нам надо минимизировать функцию
f=α(6S11+4S12+2S13+5S21+3S22+2S23), (1.4) при ограничениях: S11 + S21 =130; S12 + S22 =140; S13 + S23=140; (1.5) S11 + S12 + S13 =250; S21 + S22 + S23 =160 . Как и в предыдущем примере имеем задачу линейного программирования. Основные определения
ОПРЕДЕЛЕНИЕ 1.1.Задача, состоящая в нахождении наибольшего (наименьшего) значения функции
на множестве точек
a21x1 + a22x2 +…+ a2nxn < R2 > b2 . . . . . . . . . . (1.7) am1x1 + am2x2 +…+ amnxn < Rm > bm
называется задачей линейного программирования общего вида. Здесь: f( Ri, i = ci, i = ОПРЕДЕЛЕНИЕ 1.2.Всякую точку Задача линейного программирования состоит, таким образом, в нахождении такой допустимой точки Задачу линейного программирования, представленную в виде: f = с1x1 + c2x2 + … + cnxn → max (min)
a21x1 + … + a2nxn= b2 . . . . . . . (1.8) am1x1 + … + amnxn= bm xi ≥ 0, i =
будем считать канонической задачей линейного программирования. Введением дополнительных переменных, мы можем любое ограничение вида неравенства свести к ограничениям – равенствам. Если не на все переменные наложено требование неотрицательности (слабые ограничения), то такие переменные можно заменить разностью двух новых переменных, каждая из которых неотрицательна. Проиллюстрируем сказанное на примере. Пример 1.1. Привести к каноническому виду задачу:
f = x1 –2x1 +x3
2x1 +3x2 – 4x3 = 3 (1.9) –x1+ x2– x3 ≥ 2 x1
Введем две дополнительные неотрицательные переменные x4 и x5 в первом и третьем ограничениях, так, чтобы получить ограничения – равенства. Кроме того, переменную x3 представим в виде: x3 = x3׳ – x3״, (1.10) где: x3׳ Получим: f = x1 – 2x1 + x3׳ – x3״
2x1 + 3x2 – 4(x3׳ – x3״) = 3 (1.11) – x1 – x2 – (x3׳ – x3״) – x5 = 2 x1 ³ 0, x2 ³ 0, x3׳ ³0, x3״ ³0, x4 0, x5 а это уже задача в канонической форме. Введя в рассмотрение векторы
. . . . . . . am1 … amn
можем переписать задачу (1.6),(1.7) линейного программирования в форме:
f =
Геометрическая интерпретация двумерной задачи линейного программирования и ее решение
Рассмотрим двумерную задачу:
f = c1x1 + c2x2
a21x1 + a22 x2 < R2 > b2 . . . . . (1.15) am1 x1 + am2 x2 < Rm > bm .
Каждое из ограничений ai1x1+ai2 x2 < Ri > bi определяет в плоскости, с системой координат x1 o x2 множество точек, лежащих по одну сторону от прямой ai1x1+ai2x2=bi (т.е. полуплоскость). Множество всех точек плоскости, координаты которых удовлетворяют всем ограничениям, т.е. принадлежат сразу всем полуплоскостям, определяемым отдельными ограничениями, будет представлять собой допустимое множество. Очевидно, что, если множество не пусто, то это будет некоторый многоугольник (возможно и неограниченный, возможно вырождающийся в отрезок, точку). Многоугольник будет выпуклым, что легко показать, т.е. любые две его точки можно соединить отрезком, точки которого принадлежат допустимому множеству. ОПРЕДЕЛЕНИЕ 1.3. Множество D-точек n-мерного евклидова пространства будем называть выпуклым, если для любых x(1)=(x1(1),…,xn(1))T и x(2)=(x1(2),…,xn(2))T из множества D и любых α ≥0, β≥0 таких, что α+β=1, точка x=αx(1)+βx(2) также принадлежит D. ОПРЕДЕЛЕНИЕ 1.4. Вершиной выпуклого множества в Rn назовем такую точку, которую нельзя представить в виде x=αx(1)+βx(2), α>0, β>0, α+β=1, ни при каких x(1),x(2). Проиллюстрируем вышесказанное примерами. Примеры:изобразить множество точек, удовлетворяющих системе неравенств.
3x1 – x2£ 1 x1 – 2x2£ 1 x1 ³ 0 x2 ³ 0 x2 ³ 0
x1 + x2 £ 1 x1 + x2 ³1 x2 £1 x1 + x2 £1 x2 – x1 ³–1
Построив допустимые множества, убедимся в вышесказанном. Рассмотрим теперь геометрическую интерпретацию решения задачи линейного программирования. Пусть допустимая область задачи (1.14)−(1.15) оказалась непустой (в соответствии с рисунком 1.1).
(x1(0) , x2(0) ) – точка максимума
f=amах Точка минимума
n= grad f f = c1x1 + c2x2 = a х1
Рисунок 1.1 - Геометрическая интерпретация задачи линейного программирования
Мы хотим найти те точки допустимой области, координаты которых доставляют целевой функции наибольшее значение. Построим линию уровня целевой функции f=c1x1+c2x2=a . Получим множество точек, в точках которого f принимает одно и тоже значение a . Перемещая линию уровня в направлении вектора grad f=(c1,c2)=n, нормального к линии уровня, будем получать в пересечении этой линии с допустимой областью точки, в которых целевая функция принимает новое значение, большее чем значение на предшествующих линиях уровня. Пересечение допустимой области с линией уровня в том ее положении, когда дальнейшее перемещение дает пустое множество, и будет множеством точек максимума задачи линейного программирования. Перемещая линию уровня в направлении противоположном вектору n, аналогичным образом найдем точки минимума. Пример 1.2. f = x2 – 2x1
x1 – 2x2 £ 1 x1 ³ 0, x2 ³ 0
f =1
n (–2,1) 1 x1 –2 –1 0.5 1
Рисунок 1.2 - Геометрическая интерпретация задачи линейного программирования
Точка максимума: x=(0, 1)T; fmax=f(0, 1)=1. Легко представить, что задача имеет бесчисленное множество оптимальных решений, а может их не иметь вовсе, как например:
f = x1 + x2
–x1 + x2 £ 1 x1 – 2x2 £ 2 x1 ³ 0, x2 ³ 0.
Целевая функция достигает минимального значения в точках отрезка x1+x2=1, между точками (0, 1) и (1, 0), а максимального значения функция не достигает (не ограничена в допустимой области).
K
f=K
1 n(1,1)
–1 1 2 x1 –1
f =1
Рисунок 1.3 − Геометрическая интерпретация задачи линейного программирования
1.3.1 Свойства задачи линейного программирования
Рассмотренные примеры позволяют сформулировать основные свойства задачи линейного программирования. Свойство 1. Допустимая область задачи линейного программирования выпукла, если она не пуста. Свойство 2. Если допустимая область имеет вершины и задача линейного программирования имеет решение, то оно достигается по крайней мере в одной из вершин. Свойство 3. Множество решений задачи линейного программирования выпукло. Свойство 4. Если допустимая область ограничена, то любая задача линейного программирования имеет оптимальное решение. Свойство 5. Необходимым и достаточным условием существования решения задачи линейного программирования на максимум (минимум) является ограниченность целевой функции сверху (соответственно снизу) в допустимой области. Все перечисленные свойства справедливы и в общем случае (n≥2).
Тогда: 1) тем или иным способом находим какую-нибудь вершину допустимого множества и по определенным критериям определяем, не является ли она оптимальной. Если вершины нет, то допустимая область пуста. Если вершина оптимальна, то задача решена. Если нет, то 2) используя определенные правила проверяем, нельзя ли утверждать, что задача не имеет оптимального решения (целевая функция не ограничена сверху или, соответственно, снизу на допустимом множестве). Если утверждать это можно, то задача неразрешима. Если нельзя, то 3) по определенному правилу ищем новую, лучшую вершину и переходим к пункту 1). Итак, для реализации предложенной схемы необходимо указать способ нахождения вершины допустимого множества, критерий оптимальности или неразрешимости, способ перехода от одной вершины к другой, лучшей.
1.3.2 Обоснование симплекс метода
Пусть имеется задача линейного программирования в канонической форме:
f = c1x1 + c2x2
. . . . . . . . . (1.17) am1 x1 + … +amn xn = bm x1³0, …, xm³0 .
Вводя в рассмотрение векторы
Aj=(a1j , a2j ,…, amj )T , j=
f = ( A1x1 + A2x2 +…+ Anxn =b; (1.19) x
и трактовать ее следующим образом: из всех разложений вектора b по векторам A1,…,An , с неотрицательными коэффициентами требуется выбрать хотя бы одно такое, коэффициенты xi, i=1,n, которого доставляют целевой функции f оптимальное значение. Не ограничивая общности считаем ранг матрицы А равным m и n>m (случай n=m тривиален). Дадим ряд определений. ОПРЕДЕЛЕНИЕ 1.5. Ненулевое допустимое решение x=(x1,…,xn)T называется опорным, если векторы ОПРЕДЕЛЕНИЕ 1.6. Ненулевое опорное решение назовем невырожденным, если оно имеет точно «m» положительных координат. ОПРЕДЕЛЕНИЕ 1.7. Если число положительных координат опорного решения меньше m, то оно называется вырожденным. ОПРЕДЕЛЕНИЕ 1.7. Упорядоченный набор из «m» линейно − независимых векторов Ai, соответствующих положительным координатам опорного решения назовем базисом. Пример 1.3. Дана система ограничений задачи:
x1 − 2x3 + x4 = 1 (1.20) x1 ³0, x2 ³0, x3³0, x4 ³0.
m=2; A1= Очевидно, что x(1)=(0, 2, 0, 1)T , x(2) =(1, 0, 0, 0)T, x(3)=( Приведем теорему, увязывающую понятие опорного решения и вершины допустимого множества. ТЕОРЕМА 1.1. Вектор Доказательство. Необходимость. Пусть x – опорное решение задачи (1.19). Если x = 0, то невозможность ее представления в виде Пусть x ≠ 0 и где x1>0, x2 >0,…, xk>0. Предположим, в противоречие с теоремой, что точка x не является вершиной допустимого многогранника:
Так как последние n-k координат точки x равны нулю, то и последние n-k координат, как точки x(1), так и точки x(2) должны быть равны 0.Таким образом, можно записать:
Ввиду допустимости точек Вычитая почленно (1.22) из (1.21), получим:
Точки x(1) и x(2) различны, следовательно, среди коэффициентов при Ai (i=1,2,…,k) Достаточность. Пусть наоборот, точка x– вершина допустимого многогранника. Если x = 0, то x по условию опорное решение. Пусть, x≠0 и для определенности x=(x1,x2,…,xk,0,…,0), где x1>0, x2 >0,…,xk>0. Предположим снова от противного, что при этом вектор x=(x1,x2,…,xk,0,…,0) являясь, конечно, допустимым для нашей задачи, не является опорным решением. Тогда векторы A1, A2,…, Ak – линейно зависимы, т.е. существуют такие действительные числа α1, α2,…, αk не все равные нулю, что справедливо равенство: Являясь допустимым, вектор x удовлетворяет условию: Умножим обе части равенства (1.24) на некоторый параметр θ и сначала вычтем почленно (1.24) из (1.25), а затем сложим (1.24) и (1.25).Получим:
Так как xi >0 (i=1,2,…,k), то, очевидно, можно найти такое достаточно малое значение θ0 > 0 множителя θ, что и в первом и во втором из полученных равенств, все коэффициенты будут неотрицательными. Тогда эти равенства (при θ = θ0) означают, что n- мерные векторы
и
являются допустимыми (причем различными) решениями задачи. При этом, очевидно, имеем:
а это противоречит тому, что x– вершина допустимого многогранника. Следовательно, x не может не быть опорным решением. Теорема доказана.
Дан базис
Тогда: b= ( дополнив найденный вектор нулевыми значениями переменных ( Предварительно введем обозначения: xB= ( B =[ xD=( cB=( сD= ( D=[ С учетом введенных обозначений ограничения (1.19) можно переписать в виде: BxB+DxD=b. (1.26) Выразим базисные переменные через свободные xB=B (при xD=0 получаем базисные компоненты опорного решения). Подставим xB в целевую функцию:
f=
Обозначим: a=(a1,…,an-m)=( и назовем его вектором оценок.
Очевидно, что a xc= Отметим, что произведение а) если все компоненты вектора оценок неотрицательные, то максимальное значение целевой функции достигается при xB= б) если среди компонент вектора оценокα есть отрицательные, то опорное решение не оптимально, поскольку, как видно из (1.28)−(1.30), возможно увеличить значение f за счет некоторых компонент вектора xD; при этом возможны две ситуации: 1) отрицательны компоненты вектора оценок, к примеру, αk1, αk2,…,αks и при этом, по крайней мере у одного из свободных векторов 2) в случае положительных компонент разложения по базису свободных векторов существует лучшее опорное решение, которое можно получить, введя в базис свободный вектор где: Заменив базис, мы можем вновь перейти к построению опорного решения и его исследования. Отметим, что координаты всех векторов в новом базисе могут быть найдены через координаты векторов в старом базисе по формулам:
В итоге алгоритм решения задачи линейного программирования можно изобразить схемой, представленной на рисунке 1.4.
1.3.3 Нахождение начального базиса.
В заключении обратимся к вопросу построения начального базиса. Здесь отметим, что, если в исходной задаче все ограничения имели вид “
f =
Рисунок 1.4 – Схема алгоритма решения задачи линейного программирования
Рассмотрим вспомогательную задачу:
G = –y1 – y2 – … – ym
. . . . . . . . . . . . . am1x1 + … + amnxn + 0*y1 + …+ym = bm xi yi
Так как целевая функция этой задачи ограничена сверху нулем, то задача имеет оптимальное решение. Переменные y1, y2, ….,ym называются искусственными переменными. Очевидно, что векторы
образуют базис для опорного решения
который называют искусственным базисом. Решая вспомогательную задачу симплекс-методом, мы найдем оптимальное решение
1.3.4 Решение в форме симплекс − таблиц.
В случае небольшого числа ограничений и переменных, приведенный в предыдущем разделе алгоритм можно легко реализовать без помощи ЭВМ, оформляя решение в виде симплекс-таблиц. Итак, дана задача:
f = (
и найден исходный базис
Таблица 1.2 - Симплекс таблица
Здесь в столбце «Базис» указываются вектора |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 242. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 , (1.3)
, (1.3) f(x)=с1x1+c2x2 + … + cnхn (1.6)
f(x)=с1x1+c2x2 + … + cnхn (1.6)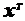 =(x1,…,xn), удовлетворяющих системе ограничений вида:
=(x1,…,xn), удовлетворяющих системе ограничений вида: a11x1 + a12x2 +…+ a1nxn < R1 > b1
a11x1 + a12x2 +…+ a1nxn < R1 > b1 )=с1 x1 + c2 x2 + … + cn xn – целевая функция;
)=с1 x1 + c2 x2 + … + cn xn – целевая функция; – операции отношения =, ≥,≤;
– операции отношения =, ≥,≤; ; aij, i =
; aij, i =  j =
j =  ; bi, i =
; bi, i =  – заданные константы.
– заданные константы. =(x1,…,xn), компоненты которой удовлетворяют всем ограничениям системы (1.7), будем называть допустимой точкой или допустимым решением задачи, или допустимым планом задачи.
=(x1,…,xn), компоненты которой удовлетворяют всем ограничениям системы (1.7), будем называть допустимой точкой или допустимым решением задачи, или допустимым планом задачи. (такого допустимого плана) среди множества допустимых точек, при которой целевая функция принимает max (min) значение. Допустимое решение
(такого допустимого плана) среди множества допустимых точек, при которой целевая функция принимает max (min) значение. Допустимое решение  a11x1 + … + a1nxn= b1
a11x1 + … + a1nxn= b1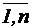 ;
; max
max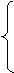 x1 + 2x2 + 3x3 ≤ 5
x1 + 2x2 + 3x3 ≤ 5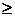 0, x2
0, x2  x1 + 2x2 + 3(x3׳ – x3״) + x4 = 5
x1 + 2x2 + 3(x3׳ – x3״) + x4 = 5 a11 … a1n
a11 … a1n =(c1, c2, … cn),
=(c1, c2, … cn), 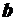 = (b1,…, bm)T, A= a21 … a2n
= (b1,…, bm)T, A= a21 … a2n  (1.13)
(1.13) a11x1 + a12 x2 < R1 > b1
a11x1 + a12 x2 < R1 > b1
 1) 2x1 – 3x2£ 2 2) –x1 + x2£ 1
1) 2x1 – 3x2£ 2 2) –x1 + x2£ 1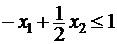 x1 ³ 0
x1 ³ 0
 3)
3) 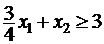 4)
4) 
 x2 f =amin
x2 f =amin –x1 + x2 £ 1
–x1 + x2 £ 1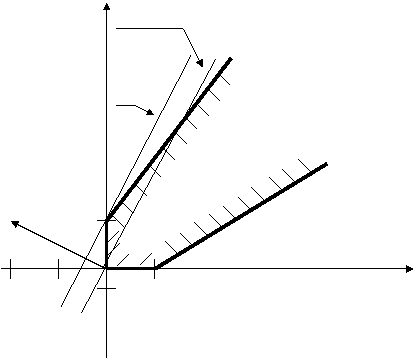 x2 f = –2x1 + x2 = 0
x2 f = –2x1 + x2 = 0 x1 + x2 ³ 1
x1 + x2 ³ 1 x2
x2 cnxn
cnxn  a11x1 + … + a1n xn = b1
a11x1 + … + a1n xn = b1 ; (1.18)
; (1.18) , соответствующие отличным от нуля координатам вектора x, линейно-независимы.
, соответствующие отличным от нуля координатам вектора x, линейно-независимы. 2x1 + x2 + 3x3 = 2
2x1 + x2 + 3x3 = 2 , A2 =
, A2 =  , A3 =
, A3 =  , A4=
, A4=  ,
,  .
. , 1, 0,
, 1, 0,  , где α >0, β >0 и
, где α >0, β >0 и  – допустимые решения, очевидна.
– допустимые решения, очевидна. ,
,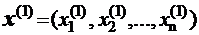 и
и  ,
,


 и
и  имеем:
имеем: (1.21)
(1.21) . (1.22)
. (1.22) . (1.23)
. (1.23) в (1.23) есть отличные от нуля. А это означает, что векторы A1, A2,…, Ak линейно зависимы, что противоречит тому, что x=(x1,x2,…,xk,0,…,0)– опорное решение задачи. Следовательно, наше предположение неверно и x вершина допустимого многогранника.
в (1.23) есть отличные от нуля. А это означает, что векторы A1, A2,…, Ak линейно зависимы, что противоречит тому, что x=(x1,x2,…,xk,0,…,0)– опорное решение задачи. Следовательно, наше предположение неверно и x вершина допустимого многогранника. . (1.24)
. (1.24) . (1.25)
. (1.25)




 ,
,  ,…,
,…,  дан. Отправляясь от него покажем, как найти опорное решение. Сформулируем условие оптимальности решения, условие отсутствия решения. Покажем, как перейти к базису, дающему лучшее решение.
дан. Отправляясь от него покажем, как найти опорное решение. Сформулируем условие оптимальности решения, условие отсутствия решения. Покажем, как перейти к базису, дающему лучшее решение.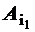 ,
,  ,…,
,…,  .
.

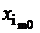
 ,…,
,…,  ), получаем опорное решение. Исследуем его на оптимальность, для этого исследуем целевую функцию.
), получаем опорное решение. Исследуем его на оптимальность, для этого исследуем целевую функцию. ,…,
,…,  )T – вектор базисных переменных;
)T – вектор базисных переменных;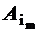 ]– матрица базисных векторов;
]– матрица базисных векторов; ,…,
,…,  ,…,
,…, 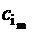 )T – вектор из коэффициентов целевой функции при базисных неизвестных;
)T – вектор из коэффициентов целевой функции при базисных неизвестных;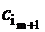 ,…,
,…,  )T – вектор из коэффициентов целевой функции при свободных переменных;
)T – вектор из коэффициентов целевой функции при свободных переменных; ,…,
,…,  ] – матрица свободных векторов (векторов, не вошедших в базис).
] – матрица свободных векторов (векторов, не вошедших в базис). (
( 
 –
–  xB+
xB+ 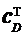 xD=
xD= 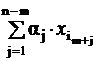 . (1.30)
. (1.30) ,
, 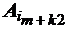 ,…,
,…,  все компоненты разложения по базису не положительны, тогда из (1.27) видно, что можно неограниченно увеличить компоненты вектора xB за счет увеличения компоненты вектора xD, а, следовательно, целевая функция не ограничена;
все компоненты разложения по базису не положительны, тогда из (1.27) видно, что можно неограниченно увеличить компоненты вектора xB за счет увеличения компоненты вектора xD, а, следовательно, целевая функция не ограничена; S, соответствующий наименьшей из отрицательных компонент вектора оценок (с целью максимально прирастить f ) и, выведя из базиса тот вектор
S, соответствующий наименьшей из отрицательных компонент вектора оценок (с целью максимально прирастить f ) и, выведя из базиса тот вектор 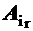 , исходного базиса, для которого:
, исходного базиса, для которого: (1.31)
(1.31) – компоненты xB;
– компоненты xB;  – компоненты вектора
– компоненты вектора  (1.32)
(1.32)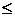 ”, то в качестве начального базиса (как легко показать) можно брать базис из векторов при дополнительных переменных. В общем случае для построения начального базиса используется специальный прием, известный как метод искусственного базиса, изложенный ниже. Итак, пусть дана задача линейного программирования в канонической форме:
”, то в качестве начального базиса (как легко показать) можно брать базис из векторов при дополнительных переменных. В общем случае для построения начального базиса используется специальный прием, известный как метод искусственного базиса, изложенный ниже. Итак, пусть дана задача линейного программирования в канонической форме:
 a11x1 + … + a1nxn + y1 = b1 (3. a21x1 + … + a2nxn + 0·y1 + y2 = b2 (1.34)
a11x1 + … + a1nxn + y1 = b1 (3. a21x1 + … + a2nxn + 0·y1 + y2 = b2 (1.34) ,
, .
. ,
, ,…,
,…,  ,
,  ,…,
,…,  ). Если в этом решении, среди искусственных переменных есть положительные, то исходная задача линейного программирования неразрешима, если же
). Если в этом решении, среди искусственных переменных есть положительные, то исходная задача линейного программирования неразрешима, если же 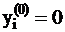 ,
,  , то базис, соответствующий оптимальному решению вспомогательной задачи, можно взять в качестве исходного базиса основной задачи.
, то базис, соответствующий оптимальному решению вспомогательной задачи, можно взять в качестве исходного базиса основной задачи. x1 +
x1 +  x2 +…+Anxn=b, (1.35)
x2 +…+Anxn=b, (1.35)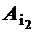 ,…,
,…, 



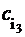


 1
1
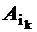 попавшие в базис; в столбце cB. записываются коэффициенты
попавшие в базис; в столбце cB. записываются коэффициенты  при соответствующих неизвестных из целевой функции; в столбце b (опорное решение) записываются координаты разложения вектора b по базису, то есть опорный план; в столбцах
при соответствующих неизвестных из целевой функции; в столбце b (опорное решение) записываются координаты разложения вектора b по базису, то есть опорный план; в столбцах