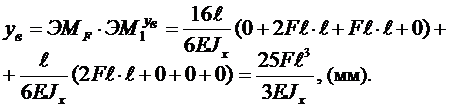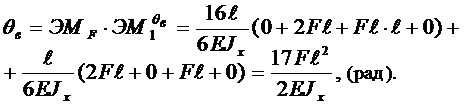Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методические указания к выполнению второй задачи ⇐ ПредыдущаяСтр 3 из 3 Использование графоаналитического способа при определении линейных или угловых перемещений позволяет заменить процесс интегрирования вычислением результата по формуле Т. Симпсона, которая включает в себя геометрические параметры построенных эпюр ЭМF и ЭМ1. Для определения перемещения произвольной точки в произвольном направлении, необходимо последовательно выполнять приведенные ниже действия. Алгоритм определения перемещений 1. Строим эпюру от внешней нагрузки МF – так называемую «грузовую» эпюру (предварительно определив опорные реакции). 2. «Снимаем» внешнюю нагрузку со стержня и в точке, перемещение которой определяем, прикладываем единичную нагрузку: единичную силу, если определяем линейное перемещение, или единичный момент, если определяем угол поворота. 3. Строим единичную эпюру М1 (предварительно определив опорные реакции). 4. Назначаем на участках построенных эпюр начало «н» и конец «к». 5. Вычисляем интеграл О. Мора, т. е. определяем искомое перемещение перемножением двух эпюр ЭМF х ЭМ1 по формуле Т. Симпсона:
или
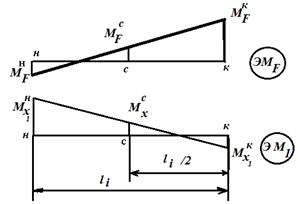
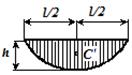
где Например, грузовая и единичная эпюры на каком-либо произвольном участке балки представлены графиками, изображенными на рисунке 1.4. Применяя формулу Т. Симпсона при перемножении эпюры МF на эпюру М1, получаем ЭМF ×ЭМ1=
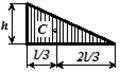
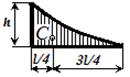
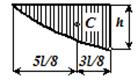
Рисунок 1.4. Вычисление интегралов О. Мора по способу А.К. Верещагина Вычисление интегралов О. Мора существенно можно упростить, если одна из эпюр прямолинейна. Такое условие всегда выполняется для систем, состоящих из прямых брусьев, так как при этом эпюры от единичной нагрузки всегда ограничены прямыми линиями. Правило А.К. Верещагина заключается в замене операции интегрирования перемножением площади эпюры моментов от внешней нагрузки на ординату линейной эпюры от единичной силы, расположенную под центром тяжести первой эпюры.  Общая формула перемещений для систем из прямолинейных элементов принимает вид
где ΩМF – площадь эпюры от внешней нагрузки ЭМF (грузовой эпюры); М1С – ордината, взятая с единичной эпюры ЭМ1, под центром тяжести грузовой эпюры ЭМF. Обратить внимание: вычисление интеграла О. Мора способом А.К. Верещагина проводят по участкам, на каждом из которых эпюра от единичной нагрузки должна быть прямолинейной. Площади некоторых простейших фигур и положения их центров тяжести приведены в таблице 1.1. Таблица 1.1. – Площади эпюр и положения их центров тяжести
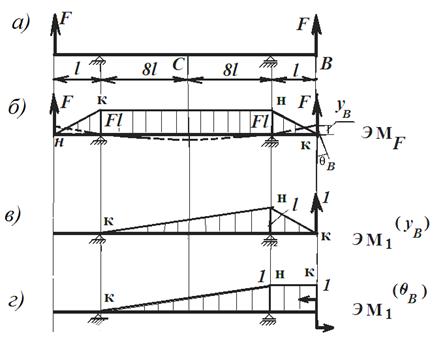
Пример решения задачи № 2. Определить в общем виде вертикальное перемещение правого края yB и угол поворота qВ концевого сечения балки (рисунок 1.5., а), изгибную жесткость сечения считать постоянной EJx = const. Расчетная схема симметрична по геометрии, нагрузкам и связям. Решение Балка работает на изгиб, поэтому в вектор линейного и углового перемещений вносит свой вклад изгибная деформация каждого из трех участков. Решение исполняется по известному алгоритму с учетом симметрии расчетной схемы. 1. По расчетной схеме от внешнего нагружения определяем реакции и строим графики изгибающего момента от внешних сил – ЭМF (рисунок 1.5., б). 2. Формируем две расчетные схемы с единичными нагружениями: первую – от нагрузки в сечении В единичной силой (рисунок 1.5., в), вторую – от нагрузки в сечении В единичным моментом (рисунок 1.5., г). На этих расчетных схемах определяются реакции от единичных нагружений и изображаются графики изгибающих моментов
Рисунок 1.5. 3. Сопоставляя графики изгибающих моментов от внешней нагрузки и от единичных нагружений, определяем число активных участков. Для определения перемещений на правом краю следует учитывать деформации двух участков – среднего длиной 16l и правого длиной l. Для угла поворота qВ активно выступают эти же участки. 4. Формируем формулу Т. Симпсона для вычисления линейного и углового перемещений:
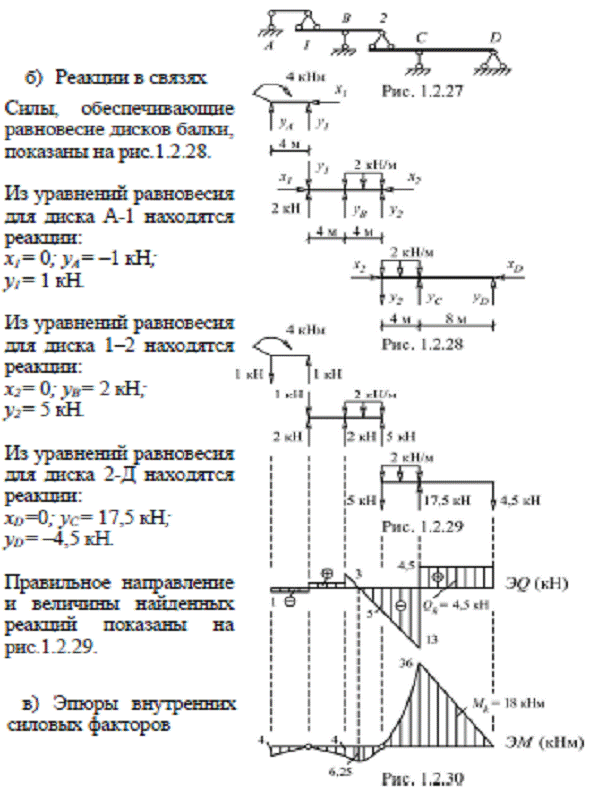
Образец решения задачи 3.Для многопролетной балки построить эпюры внутренних силовых факторов.
ЗАДАНИЯ ДЛЯ РГР
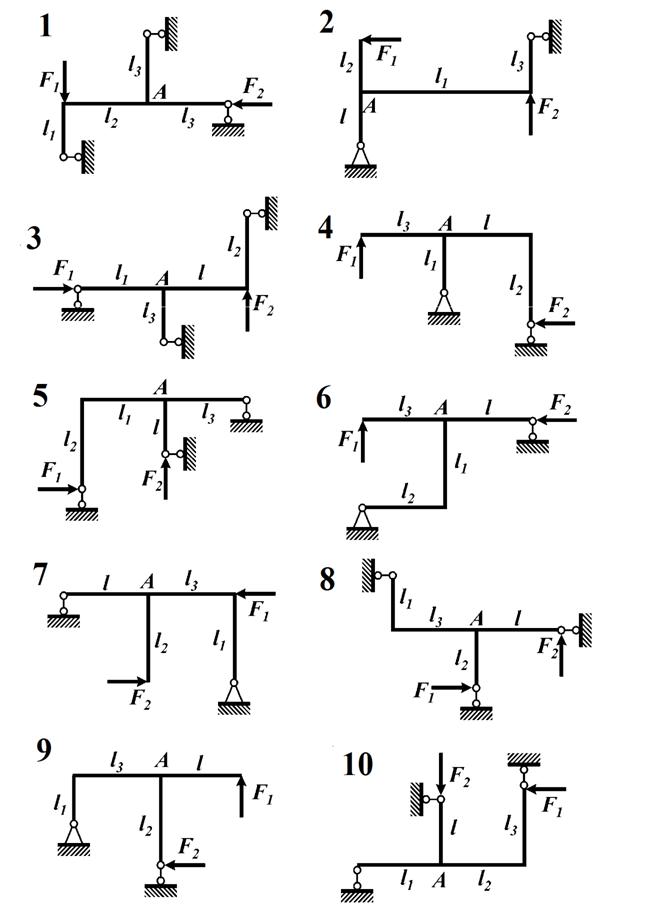
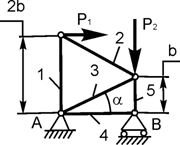
Задача 1. Для плоской рамы с шарнирными опорами (рис. 2.1., табл. 2.1.) определить опорные реакции и построить эпюры внутренних силовых факторов. Убедиться в равновесии узла А.
Таблица 2.1.
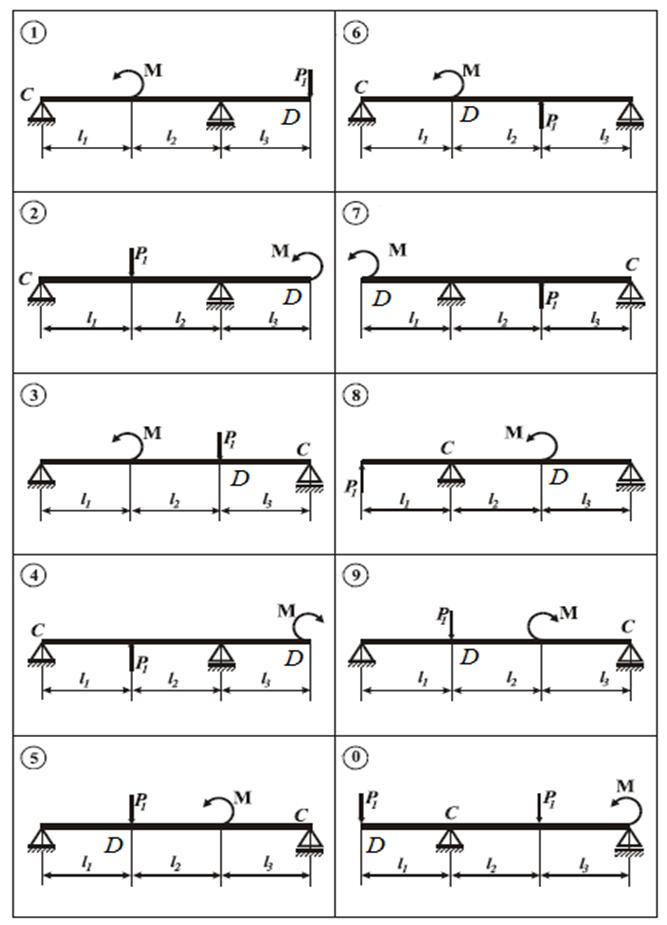
Рисунок 2.1. Задача 2. Для стальной балки (рис.2.2.) круглого поперечного сечения, нагруженной сосредоточенными силами, моментами, необходимо: - построить эпюру изгибающего момента Мх; - определить вертикальное перемещение в точке D; - определить угол поворота на опоре С. Исходные данные взять из табл. 2.2. согласно варианта. Принять для всех вариантов диаметр сечения d = 20 мм; Е = 2·105 МПа.
Таблица 2.2.
Рисунок 2.2.
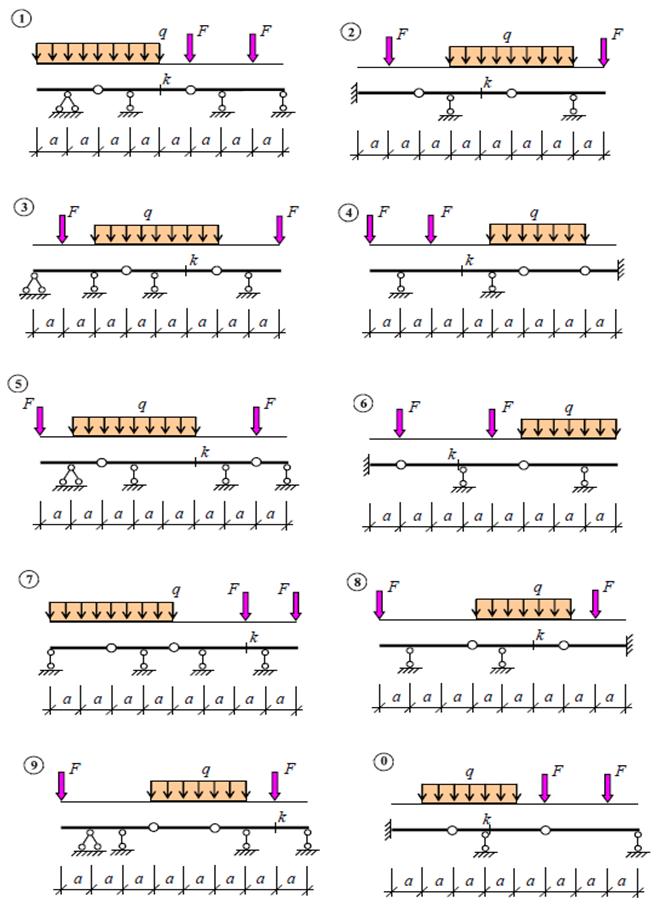
Задача № 3.Для многопролетной балки (рис. 2.3, табл. 2.3.) построить эпюры внутренних силовых факторов.
Таблица 2.3.
Рисунок 2.3.
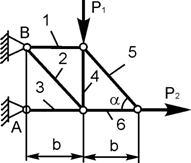
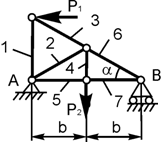
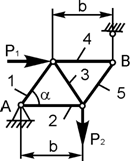
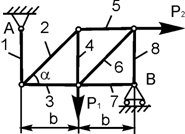
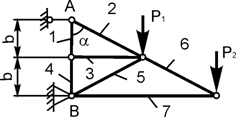
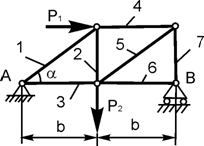
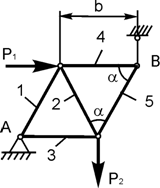
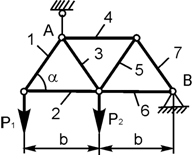
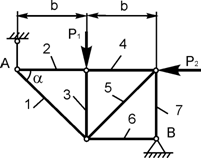
Задача 4. Определить реакции опор плоской фермы (рисунок2.4.), а также усилия в ее стержнях. Расчет выполнить методом вырезания узлов.
Рисунок 2.4.
Таблица 2.4.
Рекомендуемый список литературы Основная литература 1. Бабанов В.В. Строительная механика : учебник для студ. вузов. В 2 т. Т. 2 / В. В. Бабанов. - 2-е изд., стер. - М. : Академия, 2012. - 286 с. - (Высшее профессиональное образование. Бакалавриат. Строительство) 2. Бабанов В.В. Строительная механика : учебник для студ. вузов. В 2т. Т.1 / В. В. Бабанов. - 2-е изд., стер. - М. : Академия, 2012. - 304 с. - (Высшее профессиональное образование. Бакалавриат. Строительство) 3. Дарков А.В. Строительная механика : учебник / А. В. Дарков, Н. Н. Шапошников. - 11-е изд., стер. - СПб. ; М. ; Краснодар : Лань, 2008. - 655 с. 4. Дарков А.В. Строительная механика : учебник / А. В. Дарков, Н. Н. Шапошников. - 12-е изд., стер. - СПб. ; М. ; Краснодар : Лань, 2010. - 655 с. 5. Козырев, А. В. Механика [Электронный ресурс] : учебное пособие / А. В. Козырев. - Томск: Эль Контент, 2012. - 136 с. - 978-5-4332-0028-9. Режим доступа: http://www.biblioclub.ru/index.php?page=book&id=208680 (дата обращения 04.12.2013). 6. Кривошапко С.Н. Сопротивление материалов: лекции, семинары, расчетно-графические работы : учебник для бакалавров / С. Н. Кривошапко ; Российский университет дружбы народов. - М. : Юрайт, 2013. - 413 с. - (Бакалавр. Базовый курс) 7. Кривошапко С.Н. Строительная механика: лекции, семинары, расчетно-графические работы : учебник для бакалавров / С. Н. Кривошапко ; Российский университет дружбы народов. - 2-е изд., перераб. и доп. - М. : Юрайт, 2014. - 391 с. 8. Кривошапко С.Н. Строительная механика: лекции, семинары, расчетно-графические работы : учеб. пособие для бакалавров : учеб. пособие для студ. вузов / С. Н. Кривошапко ; Российский университет дружбы народов. - 2-е изд., перераб. и доп. - М. : Юрайт, 2011. - 391 с. - (Бакалавр). 9. Межецкий, Г. Д. Сопротивление материалов [Электронный ресурс] : учебник / Г. Д. Межецкий, Г. Г. Загребин, Н. Н. Решетник. - М.: Издательско-торговая корпорация «Дашков и К°», 2013. - 431 с. - 978-5-394-01972-2. Режим доступа: http://www.biblioclub.ru/index.php?page=book&id=135048 (дата обращения 04.12.2013). 10. Соколов, С. А. Строительная механика и металлические конструкции машин [Электронный ресурс] : учебник / С. А. Соколов. - СПб: "Политехника", 2012. - 425 с. - 978-5-7325-0969-4. Режим доступа: http://www.biblioclub.ru/index.php?page=book&id=129569 (дата обращения 04.12.2013).
Дополнительная литература 1. Далматов Б.И. Механика грунтов, основания и фундаменты (включая специальный курс инженерной геологии) : учебник / Б. И. Далматов. - 3-е изд., стер. - СПб. ; М. ; Краснодар : Лань, 2012. - 415 с. 2. Догадайло А.И. Механика грунтов: основания и фундаменты : учеб. пособие / А. И. Догадайло, В. А. Догадайло. - 2-е изд., испр. и доп. - М. : Юриспруденция, 2011. - 190 с.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 378. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

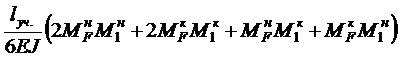
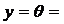
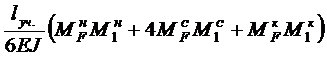 ,
,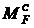 и
и 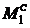 – координаты, взятые соответственно с грузовой и единичной эпюр по середине перемножаемого участка.
– координаты, взятые соответственно с грузовой и единичной эпюр по середине перемножаемого участка.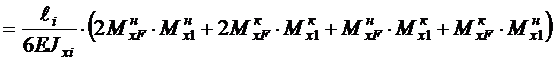 .
.
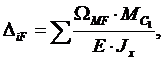
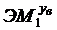 и
и 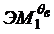 .
.