
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Прямой обмен ключами между пользователями.Два пользователя, желающие обменяться защищенной информацией, должны обладать общим секретным ключом. Для этого они должны обменяться общим ключом по безопасному каналу связи. Если пользователи меняют ключ достаточно часто, то доставка ключа превращается в серьезную проблему. Для решения этой проблемы есть два способа: 1) использование криптосистемы с открытым ключом для шифрования и передачи секретного ключа симметричной криптосистеме 2) использование системы открытого распределения ключей Диффи-Хеллмана Более практичен способ Диффи-Хеллмана, который основан на применении системы открытого распределения ключей, которая позволяет пользователям обмениваться ключами по незащищенным каналам связи. Алгоритм открытого распределения ключей Диффи-Хеллмана Предположим, что два пользователя А и В хотят организовать защищенный коммуникационный канал. 1. Обе стороны заранее уславливаются о модуле 2. Затем пользователи А и В независимо друг от друга выбирают собственные секретные ключи 3. Далее пользователь А вычисляет открытый ключ 4. Затем стороны А и В обмениваются вычисленными значениями открытых ключей 5. Далее пользователи А и В вычисляют общий секретный ключ: пользователь А: пользователь В: При этом  Ключ К может использоваться в качестве общего секретного ключа (ключа шифрования ключей) в симметричной криптосистеме. (43-45???). Элементы теории чисел. При разработке алгоритмов шифрования используется ряд понятий теории чисел и модулярной арифметики. Теория чисел изучает свойства целых чисел. Особое место среди целых чисел занимают натуральные числа – целые положительные числа 1, 2, 3, 4, … Целые числа образуют бесконечный ряд (множество) Z, где выполняются основные арифметические операции: сложение, вычитание и умножение. Натуральное число p называется простым, если p > 1 и не имеет положительных делителей, отличных от 1 и p. Натуральное число N называется составным, если N > 1 и имеет, по крайней мере, один положительный делитель, отличный от 1 и N. Функция Эйлера φ(n) — мультипликативная арифметическая функция, равная количеству натуральных чисел, меньших n и взаимно простых с ним. При этом полагают, что число 1 взаимно просто со всеми натуральными числами, и φ(1) = 1. Функция Эйлера находит применение в вопросах, касающихся теории делимости и вычетов, теории чисел, криптографии. Функция Эйлера играет ключевую роль в алгоритме RSA. Ма́лая теоре́ма Ферма́ — классическая теорема теории чисел, которая утверждает, что если p — простое число, и а не делится на р, то ар-1=1 (mod p).Равносильная формулировка: для любого простого р и целого а:(ар-а) делится на р. Это утверждение используется в системе шифрования с открытым ключом RSA. Если p— простое число, отличное от 2 и 5, то число, запись которого состоит из одних девяток, делится на N. Этот факт используется в теории признаков делимости и периодических дробей. Малая теорема Ферма является частным случаем теоремы Эйлера, которая, в свою очередь, является частным случаем теорем Кармайкла и Лагранжа для конечных циклических групп
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 505. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
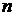 (
(  также должно быть простым) и элементе
также должно быть простым) и элементе  ,
,  . Эти числа могут не храниться в секрете. Как правило, эти значения являются общими для всех пользователей системы.
. Эти числа могут не храниться в секрете. Как правило, эти значения являются общими для всех пользователей системы.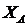 и
и  (
(  , а пользователь В - открытый ключ
, а пользователь В - открытый ключ  .
. и
и 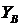 по незащищенному каналу.
по незащищенному каналу.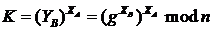 ,
, .
. , так как
, так как  .
.