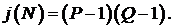Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
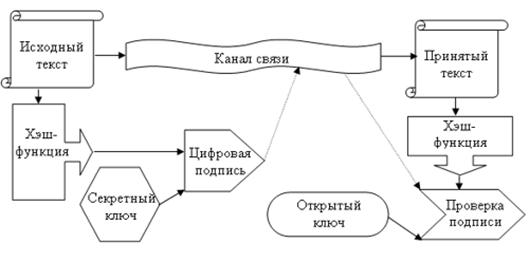
Алгоритм электронной цифровой подписи RSA.
произведение Далее отправитель вычисляет число Е. Пара чисел (Е, N) является открытым ключом. Эту пару чисел автор передает партнерам для проверки его цифровых подписей. Создаётся секретный ключ D. Если, отправитель хочет подписать сообщение М перед его отправкой - сначала сообщение М сжимают с помощью хэш-функции h() в целое число m = h(М).Затем вычисляют цифровую подпись S под электронным документом М, используя хэш-значение m и секретный ключ D: S = mD (mod N). Пара (М, S) передается партнеру-получателю как документ М, подписанный цифровой подписью S, причем подпись S сформирована обладателем секретного ключа D. После приема пары (М, S) получатель вычисляет хэш-значение сообщения М двумя разными способами: 1) восстанавливает хэш-значение m', с использованием открытого ключа Е: m' = SE (mod N). 2) находит результат хэширования принятого сообщения М с помощью такой же хэш-функции h(): m = h(М). Открытый ключ Е иногда называют "идентификатором" подписавшего. Алгоритм электронной цифровой подписи Эль Гамаля. EGSA (алгоритм цифровой подписи Эль Гамаля) - для обоснования практической невозможности фальсификации цифровой подписи может быть использована более сложная вычислительная задача, чем разложение на множители большого целого числа,- задача дискретного логарифмирования. Отсутствует возможность подделки цифровой подписи под некоторыми сообщениями без определения секретного ключа. Для генерации пары ключей (открытый ключ - секретный ключ), сначала выбирают некоторые большие простые целые числа Р(~10308 или ~21024) и G(~10154 или ~2512), причем G < Р. Они не являются секретными.  Отправитель выбирает случайное целое число X, 1<Х<(Р-1), и вычисляет Y=GXmod Р. Число Y является открытым ключом, используемым для проверки подписи отправителя. Число Y открыто, а Х является секретным ключом отправителя для подписывания документов. Для того чтобы подписать сообщение М, сначала отправитель хэширует его с помощью хэш-функции h(•) в целое число m: m = h(М), 1 < m < (Р-1) , и генерирует случайное целое число К, 1 < К < (Р-1). Затем отправитель вычисляет целое число а = GK mod Р, и, применяя расширенный алгоритм Евклида, вычисляет с помощью секретного ключа Х целое число b из уравнения m = Х * а + К * b (mod (Р-1)) . Следует отметить, что выполнение каждой подписи по методу Эль Гамаля требует нового значения К. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 605. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
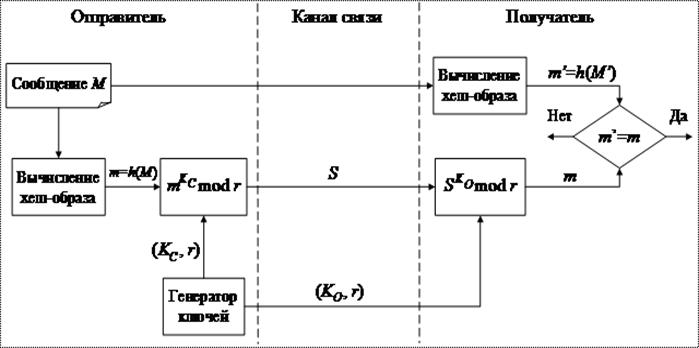
 Необходимо вычислить пару ключей (секретный ключ и открытый ключ). Для этого отправитель документов вычисляет два больших простых числа Р и Q, затем находит их
Необходимо вычислить пару ключей (секретный ключ и открытый ключ). Для этого отправитель документов вычисляет два больших простых числа Р и Q, затем находит их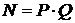 и значение функции
и значение функции