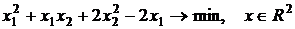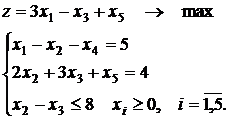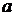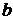Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дифференциальная геометрия и топология ⇐ ПредыдущаяСтр 4 из 4
1. Пусть X есть R, а τ состоит из: а) пустого множества и всевозможных бесконечных множеств; б) пустого множества и дополнений всевозможных конечных множеств. Является ли в этих случаях набор τ топологией в R. 2. Какие из следующих множеств попарно гомеоморфны: (-
3. Пусть А и В – компактные подмножества топологического пространства X. Верно ли, что множество А
4. Найти кривизну кривой 5. Найти под каким углом пересекаются линии
Дифференциальные уравнения 1. Проинтегрировать следующие системы дифференциальных уравнений:
2. Проинтегрировать следующую систему дифференциальных уравнений:
3. Найти решение указанной ниже задачи:
4. Найти решение указанной ниже задачи:
5. Найти решение указанной ниже задачи:
6. Найти решение указанной ниже задачи:
7. Найти решение указанной ниже задачи:
8. Найти решение указанной ниже задачи:
9. Проинтегрировать следующее уравнение:
Уравнения математической физики 1. Решите задачу Коши:
2. Приведите уравнение к каноническому виду:
3. Приведите уравнение к каноническому виду:
4. Решите задачу Коши:
5. Решите задачу Коши:
Теоретическая механика 1. Диск радиуса
2. Дифференциальное уравнение колебательного движения материальной точки имеет вид 
3. Тело массой
Вариационное исчисление 1. Найти экстремаль функционала
Методы оптимизации 1. Решить графическим способом
2. Улучшить план методом наискорейшего спуска (одна итерация).
3.Решить симплекс-методом
Методы вычислений и вычислительный практикум 1. Используя первую интерполяционную формулу Ньютона для равноотстоящих узлов вычислить приближённое значение функции в точке х*. х* = 1,25
2. Вычислить интеграл по обобщенной формуле трапеций, разбив отрезок интегрирования на 4 равные части.
3. Применяя метод Эйлера, решить задачу Коши на отрезке [0,1], разбив его на 4 равные части.
|
||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 384. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
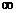 ;3]; [1;5) ; (-7; 2) и [2, 3]. Рассматривается естественная топология.
;3]; [1;5) ; (-7; 2) и [2, 3]. Рассматривается естественная топология.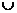 В компактно? Верно ли, что множество А
В компактно? Верно ли, что множество А 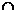 В компактно ?
В компактно ?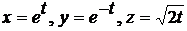 в точке
в точке 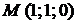 .
.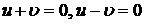 на прямом геликоиде
на прямом геликоиде 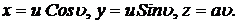
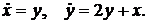
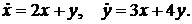
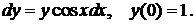
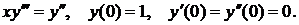
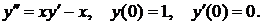
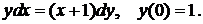
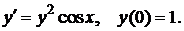
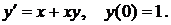
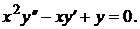

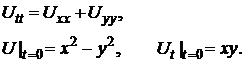
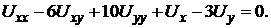
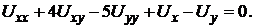
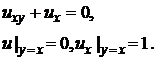
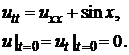
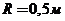 катится без скольжения по плоскости. Скорость центра диска
катится без скольжения по плоскости. Скорость центра диска 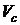 равна 2 м/с. Определить угловую скорость вращения диска.
равна 2 м/с. Определить угловую скорость вращения диска.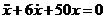 . Определить период затухающих колебаний.
. Определить период затухающих колебаний.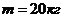 падает по вертикали, сила сопротивления воздуха
падает по вертикали, сила сопротивления воздуха 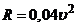 . Определить максимальную скорость падения тела.
. Определить максимальную скорость падения тела.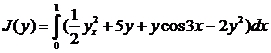 .
. 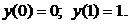
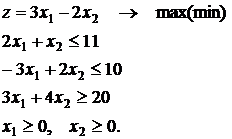
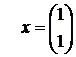 задачи на безусловный минимум
задачи на безусловный минимум