Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Уравнения математической физики1. Классификация дифференциальных уравнений второго порядка в частных производных. Понятие корректности задачи для уравнений математической физики. Пример Адамара.
2. Задачи Коши. Метод характеристик. Формула Даламбера.
3. Смешанная задача. Метод Фурье для уравнения колебаний струны.
4. Гармонические функции и их свойства. Задачи Дирихле и Неймана. Решение задачи Дирихле для круга.
Теоретическая механика
1. Способы задания движения точки. Вычисление скорости и ускорения материальной точки при различных способах задания движения.
2. Основные теоремы динамики точки: теорема об изменении кинетической энергии, теорема об изменении количества движения и теорема об изменении кинетического момента.
3. Теорема о движении центра масс системы материальных точек.
Методика преподавания математики и информатики 1. Методы обучения в информатике. Классификация. Организационные формы обучения.
2. Методика введения действительного числа.
3. Методика введения понятия функции.
4. Методика обучения основным принципам работы на персональном компьютере. Программное обеспечения школьных персональных ЭВМ. Методы вычислений и вычислительный практикум 1. Интерполирование функций (постановка задачи; единственность интерполяционного многочлена; формула Лагранжа). 2. Численное интегрирование (квадратурные формулы трапеций и Симпсона; погрешность). 3. Одношаговые методы решения задачи Коши для обыкновенных дифференциальных уравнений первого порядка.
Вариационное исчисление 1. Условие Эйлера для основной задачи вариационного исчисления. 
Методы оптимизации
1. Симплекс-метод (критерий оптимальности, алгоритм).
2. Принцип Лагранжа снятия ограничений (для задач с ограничениями в виде равенств). ЛИТЕРАТУРА Математический анализ 1. Никольский С.М. Курс математического анализа: Учеб.пособие в 2-х томах, 3-е издание. М., Наука, 1983. 2. Кудрявцев Л.Д. Курс математического анализа: Учебник в 2-х т. М. Высш.школа. 1981. 3. Зорич В.А. Математический анализ: Учебник в 2-х т. М.: Наука, 1981, 1984. 4. Рудин У. Основы математического анализа. М.: Мир, 1976. 319 с.
Функциональный анализ и интегральные уравнения 1. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа: Учебное пособие. М.: Наука.– 1981.– 542 с. 2. Антоневич А.Б., Радыно Я.В. Функциональный анализ и интегральные уравнения. Мн.:БГУ. – 2003. – 430 с. 3. Садовничий В.А. Теория операторов: Учебное пособие. М.: Изд-во Моск. Ун-та.– 1979.– 296 с. 4. Миротин А.Р. Функциональный анализ: мера и интеграл (допущено МО РБ в качестве учебного пособия для университетов) / М. : Книжный дом «ЛИБРОКОМ», 2012. – 160 c. Теория функций комплексного переменного 1. Привалов И.И. Введение в теорию комплексного переменного: Учебн. М.: Наука, 1984, 43 с. 2. Маркушевич А.И. Краткий курс теории аналитических функций: Учебное пособие. М.: Наука, 1978, 387 с. 3. Шабат Б.В. Введение в комплексный анализ: Учебник, в 2-х ч. 2-е изд., переработанное и дополн. М.: Наука, 1976. 4. Евграфов М.А. Аналитические функции: Учебник. М., Наука, 1968, 471 с.
Теоретическая механика 1. Бухгольц, Н.Н. Основной курс теоретической механики: В 2-х ч. [Текст] / Н.Н.Бухгольц – М.: Наука, 1972. 2. Тарг, С.М. Краткий курс теоретической механики [Текст] / С.М.Тарг – М.: Наука, 1976. 3. Яблонский, А.А. Курс теоретической механики, ч. 1, 2. [Текст] / А.А.Яблонский – М.: Наука, 1971.
Алгебра и теория чисел. Аналитическая геометрия 1. Монахов В.С., Бузланов А.В. Алгебра и теория чисел : Практикум : учебное пособие. В 2-х частях. Ч.1. – Мн.: Изд. центр БГУ, 2007 г. 2. Милованов М.В., Тышкевич Р.И., Феденко А.С. Алгебра и аналитическая геометрия. – Мн.: Амалфея, 2001 г. 3. Виноградов И.М. Основы теории чисел. – М.: Наука, 1972 г. 4. Дубровин Б.А., Новиков С.П., Фоменко А.Г. Современная геометрия. – М.: Наука, 1979 г. Дифференциальная геометрия и топология 1. Кононов С.Г., Прасолов А.В., Тимохович В.Л., Тралле А.Е., Феденко А.С. Топология. – Минск, “Вышэйшая школа”, 1990. 5. Феденко А.С., Фоменко А.Т. Курс дифференциальной геометрии. :МГУ, 1980. 2. Мищенко А.С., Фоменко А.Т. Курс дифференциальной геометрии и топологии. – М.: МГУ, 1980. 3. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа : Учебное пособие, М.: Наука, 1981, 542 с. Дифференциальные уравнения 1. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. Минск: Вышэйшая школа, 1974. 2. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М.: 1984. Уравнения математической физики 1. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1977. 2. Бицадзе А.В. Уравнения математической физики. М.: Наука, 1982. 3. Петровский И.Г. Лекции об уравнениях с частными производными. М.: Л.1950.
Теория вероятностей и математическая статистика 1. Гнеденко Б.В. Курс теории вероятностей. М.: Наука, 1969. 2. Крамер Г. Математические методы статистики. М.: Мир, 1975.
Методы вычислений и вычислительный практикум 1. Бахвалов Н.С. Численные методы. М.Наука, 1975. 2. Березин Н.С., Жидков Н.П. Методы вычислений. 1 и 2-й том. М.Наука, 1966. 3. Демидович Б.П., Марон И.А. Основы вычислительной математики.- М.: Наука, 1970.
Методика преподавания математики и информатики 1. Бочкин А.И. Методика преподавания информатики. – Мн.: Выш.шк., 1998. – 431 с. 2. Быдакоров Ю.А. и др. Информатика: Учебное пособие для 8-го (9-го) кл. общеобразовательных школ. – Мн.: Народная асвета, 2000(2001). – 191 с. (230 с.). Методы оптимизации 1. Габасов Р., Кириллова Ф.М. Методы оптимизации. Минск,1981. ПЕРЕЧЕНЬ ЗАДАЧ Математический анализ
1. Найти предел
2. Найти пределы
3. Найти точки разрыва функции
4. Является ли функция
5. Проведя исследование, построить график функции
6. Вычислить следующие интегралы: а)
7. Найти
8. Вычислить
9. Найти площадь фигуры, ограниченной кривыми y = 3x – x2 , x + y = 0.
10. Исследовать сходимость интеграла
11. Найти 12. Найти:
13. Исследовать на сходимость
14. Исследовать на сходимость ряд
15. Исследовать на сходимость
16. Найти область сходимости функционального ряда
17. Исследовать на равномерную сходимость ряд в указанном промежутке
18. Написать ряд Фурье функции
19. Найти
20. Найти дифференциал
21. Изменить порядок интегрирования в повторном интеграле
22. Вычислить а) ОА - отрезок прямой линии; б) ОА - парабола, ось которой есть OY; в) ОА - ломаная линия, состоящая из отрезка ОВ оси ОХ и отрезка ВА, параллельного оси OY.
23. Применяя формулу Грина, вычислить криволинейный интеграл
24. Вычислить пределы:
а)
25. Существуют ли такие числа a и b, при которых функция
всюду дифференцируема?
26. Исследовать на дифференцируемость функцию
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 594. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
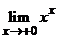 .
.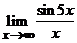 ,
, 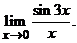
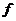 , установить их род и указать скачки в точках разрыва первого рода, если
, установить их род и указать скачки в точках разрыва первого рода, если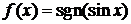 .
.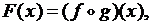

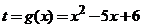 непрерывной на
непрерывной на  ? Дифференцируемой на
? Дифференцируемой на  .
.
 б)
б) 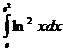 .
. где
где 
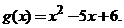
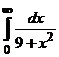 .
.
 , если
, если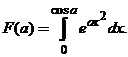
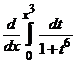 .
.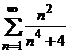 .
.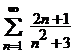 .
. .
.  его сумму и исследовать эту сумму на непрерывность
его сумму и исследовать эту сумму на непрерывность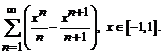
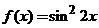 на отрезке
на отрезке 
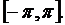
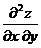 , если
, если 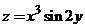 .
.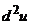 , если u = x3 + y3 + 3xy(x - y)
, если u = x3 + y3 + 3xy(x - y)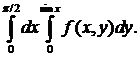
 , где О – начало координат и A (1,4), по следующим кривым:
, где О – начало координат и A (1,4), по следующим кривым: , где
, где 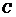 – окружность с уравнением x2 + y2 = 1.
– окружность с уравнением x2 + y2 = 1.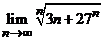 ; б)
; б)  .
.